动态规划---例题2.最长公共子序列问题

article/2025/9/6 15:40:36

本题与力扣主站1143题相同.

一.问题描述

一个给定序列的子序列是在该序列中删去若干元素后得到的序列。
确切地说，若给定序列X=<x1, x2,…, xm>，则另一序列Z=<z1, z2,…, zk>是X的子序列是指存在一个严格递增的下标序列 <i1, i2,…, ik>，使得对于所有j=1,2,…,k有

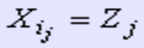
例如，序列Z=<B,C,D,B>是序列X=<A,B,C,B,D,A,B>的子序列，相应的递增下标序列为<2, 3, 5, 7>。

给定两个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时，称Z是序列X和Y的公共子序列。
例： X=<A, B, C, B, D, A, B>
Y=<B, D, C, A, B, A>
Z1=<B, C, A>
Z2= <B, C, B, A>
Z1和Z2是X和Y的一个公共子序列，而且Z2是X和Y的一个最长公共子序列，因为X和Y没有长度大于4的公共子序列。(不唯一!)

最长公共子序列(LCS)问题：给定两个序列X=<x1, x2, …, xm>和Y=<y1, y2, … , yn>，要求找出X和Y的一个最长公共子序列。

二.解题思路

穷举搜索法：对X的每一个子序列，检查它是否也是Y的子序列，并选出最长的公共子序列。X的一个子序列相应于下标序列{1, 2, …, m}的一个子序列，因此，X共有2m个不同子序列，从而穷举搜索法需要指数时间。

下面我们来考虑用动态规划法解最长公共子序列问题.此问题是动态规划的典型应用之一.

1.分析最优解的结构

定理:LCS具有最优子结构
设序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的一个最长公共子序列Z=<z1, z2, …, zk>，则：

若xm=yn，则zk=xm=yn且Zk-1是Xm-1和Yn-1的最长公共子序列；
2.若xm≠yn 且 zk≠xm ，则Z是Xm-1和Y的最长公共子序列；
3.若xm≠yn 且 zk≠yn ，则Z是X和Yn-1的最长公共子序列。

其中Xm-1=<x1, x2, …, xm-1>，Yn-1=<y1, y2, …, yn-1>，Zk-1=<z1, z2, …, zk-1>。

证明如下(反证法):

已知xm=yn ，假如zk≠xm，则<z1, z2, …, zk ,xm >是X和Y的长度为k十1的公共子序列。
这与Z是X和Y的一个最长公共子序列矛盾。因此，必有zk=xm=yn.Zk-1是Xm-1和Yn-1的一个长度为k-1的公共子序列。若Xm-1和Yn-1有一个长度大于k-1的公共子序列W，则将xm加在其尾部将产生X和Y的一个长度大于k的公共子序列。此为矛盾。
故Zk-1是Xm-1和Yn-1的一个最长公共子序列。
已知xm≠yn, zk≠xm ,Z是Xm-1和Y的最长公共子序列。假如Z不是Xm-1和Y的最长公共子序列。
zk≠xmàZ是Xm-1和Y的一个公共子序列. 若Xm-1和Y有一个长度大于k的公共子序列W，则W也是X和Y的一个长度大于k的公共子序列。这与Z是X和Y的一个最长公共子序列矛盾。由此即知Z是Xm-1和Y的一个最长公共子序列。
与2类似。

这说明：两个序列的最长公共子序列包含了这两个序列的前缀的最长公共子序列。因此，最长公共子序列问题具有最优子结构性质。

2.建立递归关系

由最长公共子序列问题的最优子结构性质可知，要找出X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的最长公共子序列，可按以下方式递归地进行:

当xm=yn时，{Xm-1和Yn-1的最长公共子序列}的末尾加上 xm
当xm≠yn时，Max{Xm-1和Y的一个最长公共子序列，X和Yn-1的一个最长公共子序列}

由此递归结构容易看到最长公共子序列问题具有子问题重叠性质。例如，在计算X和Y的最长公共子序列时,可能要计算出X和Yn-1及Xm-1和Y的最长公共子序列。而这两个子问题都包含一个公共子问题，即计算Xm-1和Yn-1的最长公共子序列。

根据子问题的最优值的递归关系,我们用c[i,j]记录序列Xi和Yj的最长公共子序列的长度。其中Xi=<x1, x2, …, xi>，Yj=<y1, y2, …, yj>。当i=0或j=0时，空序列是Xi和Yj的最长公共子序列，故c[i,j]=0。其他情况下，可建立递归关系如下：
在这里插入图片描述

3.计算最优值

直接利用(2.2)式容易写出一个计算c[i,j]的递归算法，但其计算时间是随输入长度指数增长的。由于在所考虑的子问题空间中，总共只有θ(m*n)个不同的子问题，因此，用动态规划算法自底向上地计算最优值能提高算法的效率。

c[i,j]存储Xi与Yj的最长公共子序列的长度，X和Y的最长公共子序列的长度记录于c[m,n]中
b[i,j]记录指示c[i,j]的值是由哪一个子问题的解达到的，这在构造最长公共子序列时要用到.

4.构建最长公共子序列

LCS_length产生数组b用于构造序列<x1 …, xm>和<y1, …, yn>的最长公共子序列。
首先从b[m,n]开始，沿着其中的箭头所指的方向在数组b中搜索。

当b[i,j]="1"时，表示Xi与Yj的最长公共子序列是由Xi-1与Yj-1的最长公共子序列在尾部加上xi得到的子序列；
当b[i,j]="2"时，表示Xi与Yj的最长公共子序列和Xi-1与Yj的最长公共子序列相同；
当b[i,j]="3"时，表示Xi与Yj的最长公共子序列和Xi与Yj-1的最长公共子序列相同。

代码如下:

// // 最长公共子序列
#include<bits/stdc++.h>
using namespace std;
const int Size = 1010;   //尽量用全局变量
int DP[Size][Size];
int DIR[Size][Size];    
int LCS_length(string a, string b)
{int M = a.size();int N = b.size();for(int i=1; i<=M; i++){for(int j=1; j<=N; j++){if(a[i-1] == b[j-1]) {DP[i][j] = DP[i-1][j-1] + 1;DIR[i][j] = 1;}else if(DP[i-1][j] >= DP[i][j-1]){DP[i][j] = DP[i-1][j];DIR[i][j] = 2;}else{DP[i][j] = DP[i][j-1];DIR[i][j] = 3;}}}return DP[M][N];
}
void LCS(string a, int i, int j)
{if(i==0 || j==0) return;if(DIR[i][j] == 1) {LCS(a, i-1, j-1);cout<<a[i-1];  //a[i-1]==b[j-1]}else if(DIR[i][j]==2) LCS(a, i-1, j);else if(DIR[i][j]==3) LCS(a, i, j-1);
}
void LCS2(string a, string b, int i, int j)  //算法改进,不使用DIR数组,仅仅依靠DP数组以及a,b两个序列
{if(i==0 || j==0) return;if(a[i-1]==b[j-1]){LCS2(a, b, i-1, j-1);cout<<a[i-1]<<endl;}else if(DP[i-1][j] > DP[i][j-1]) LCS2(a, b, i-1, j);else LCS2(a, b, i, j-1);
}
int main()
{string a, b;cout<<"请输入两个字符串:"<<endl;while(cin>>a>>b && a!="GG"){cout<<"最大公共子序列长度为:"<<LCS_length(a, b)<<endl;// LCS(a, a.size(), b.size());cout<<"最大公共子序列为:";LCS2(a, b, a.size(), b.size());cout<<endl<<"请输入两个字符串:"<<endl;}system("pause");return 0;
}
//www.pgcode.top 版权所有