目录
相关概念
子序列形式化定义:
公共子序列定义:
最长公共子序列(以下简称LCS):
方法
蛮力法求解最长公共子序列:
动态规划求解最长公共子序列:
分析规律:
做法:
伪代码:
下面演示下c数组的填表过程:(以求ABCB和BDCA的LCS长度为例):
时间复杂度:
代码:
结果示例:
相关概念
子序列形式化定义:
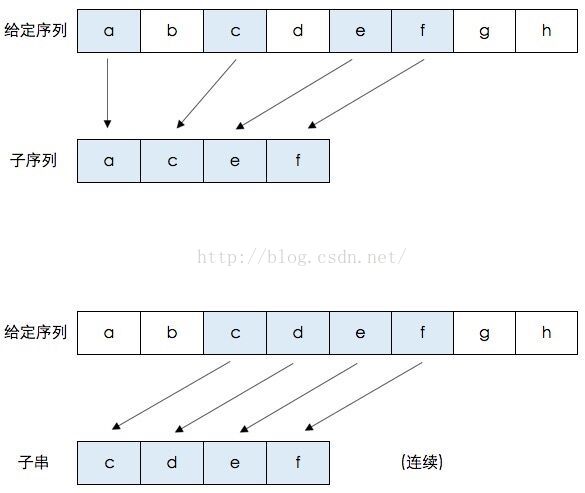
给定一个序列X=<x1,x2,x3,x4...,xm>,另一个序列Z=<z1,z2,z3,z4...,zk>,若存在一个严格递增的X的下标序列<i1,i2,i3,...,ik>对所有的1,2,3,...,k,都满足x(ik)=zk,则称Z是X的子序列
比如Z=<B,C,D,B>是X=<A,B,C,B,D,A,B>的子序列
公共子序列定义:
如果Z既是X的子序列,又是Y的子序列,则称Z为X和Y的公共子序列
最长公共子序列(以下简称LCS):
2个序列的子序列中长度最长的那个
方法
蛮力法求解最长公共子序列:
需要遍历出所有的可能,时间复杂度是O(n³),太慢了
动态规划求解最长公共子序列:
分析规律:
设X=<x1,x2,x3,x4...,xm>,Y=<y1,y2,y3,y4...,yn>为两个序列,Z=<z1,z2,z3,z4...,zk>是他们的任意公共子序列
经过分析,我们可以知道:
1、如果xm = yn,则zk = xm = yn 且 Zk-1是Xm-1和Yn-1的一个LCS
2、如果xm != yn 且 zk != xm,则Z是Xm-1和Y的一个LCS
3、如果xm != yn 且 zk != yn,则Z是X和Yn-1的一个LCS
所以如果用一个二维数组c表示字符串X和Y中对应的前i,前j个字符的LCS的长度话,可以得到以下公式:
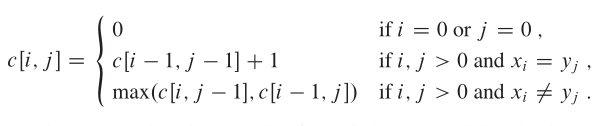
文字意思就是:
设
p1表示X的前 i-1 个字符和Y的前 j 个字符的LCS的长度
p2表示X的前 i 个字符和Y的前 j-1 个字符的LCS的长度
p表示X的前 i-1 个字符和Y的前 j-1 个字符的LCS的长度
p0表示X的前 i 个字符和Y的前 j 个字符的LCS的长度
如果X的第 i 个字符和Y的第 j 个字符相等,则p0 = p + 1
如果X的第 i 个字符和Y的第 j 个字符不相等,则p0 = max(p1,p2)
做法:
因此,我们只需要从c[0][0]开始填表,填到c[m-1][n-1],所得到的c[m-1][n-1]就是LCS的长度
但是,我们怎么得到LCS本身而非LCS的长度呢?
也是用一个二维数组b来表示:
在对应字符相等的时候,用↖标记
在p1 >= p2的时候,用↑标记
在p1 < p2的时候,用←标记
伪代码:

若想得到LCS,则再遍历一次b数组就好了,从最后一个位置开始往前遍历:
如果箭头是↖,则代表这个字符是LCS的一员,存下来后 i-- , j--
如果箭头是←,则代表这个字符不是LCS的一员,j--
如果箭头是↑ ,也代表这个字符不是LCS的一员,i--
如此直到i = 0或者j = 0时停止,最后存下来的字符就是所有的LCS字符
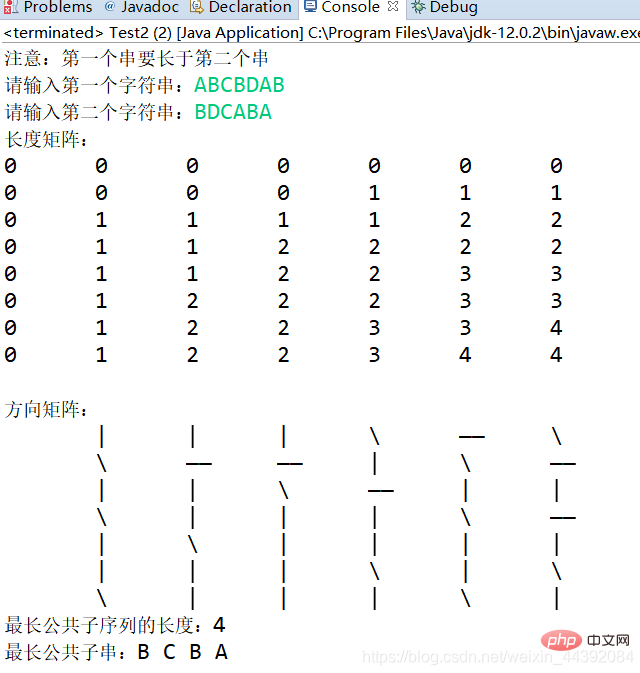
比如说求ABCBDAB和BDCABA的LCS:
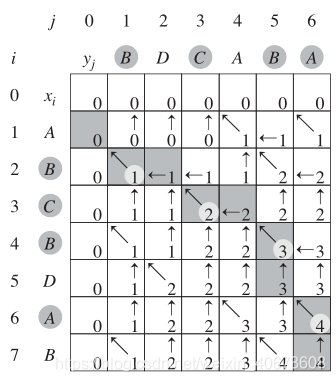
灰色且带↖箭头的部分即为所有的LCS的字符
下面演示下c数组的填表过程:(以求ABCB和BDCA的LCS长度为例):

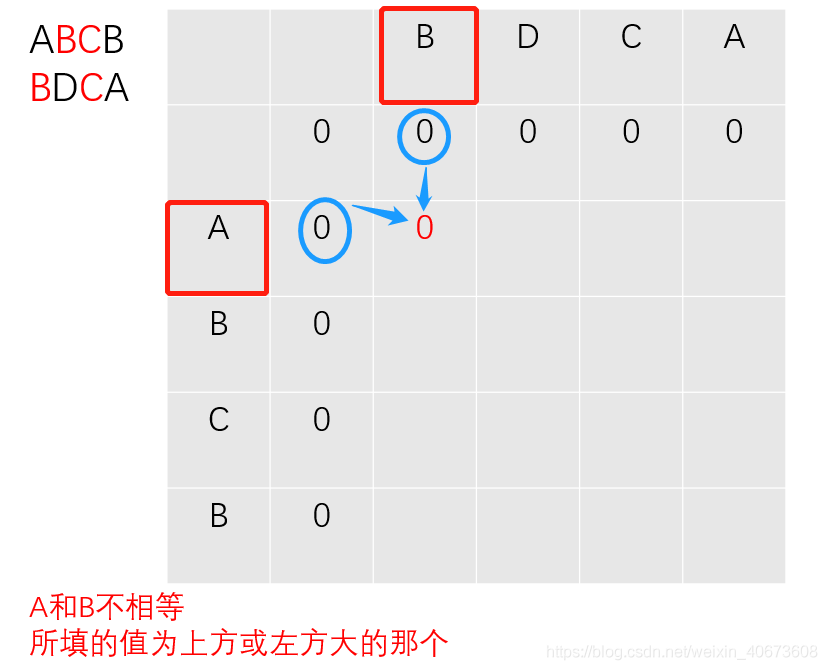
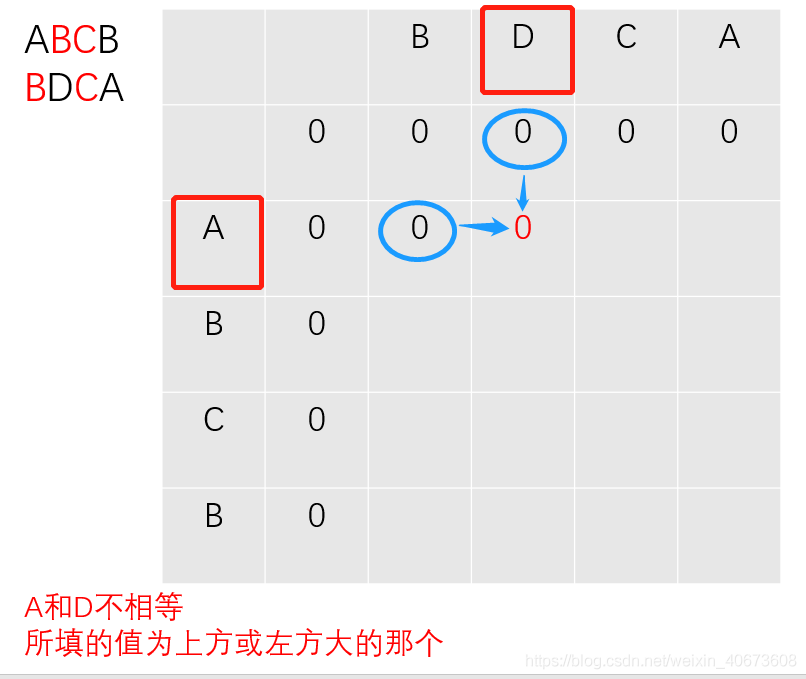
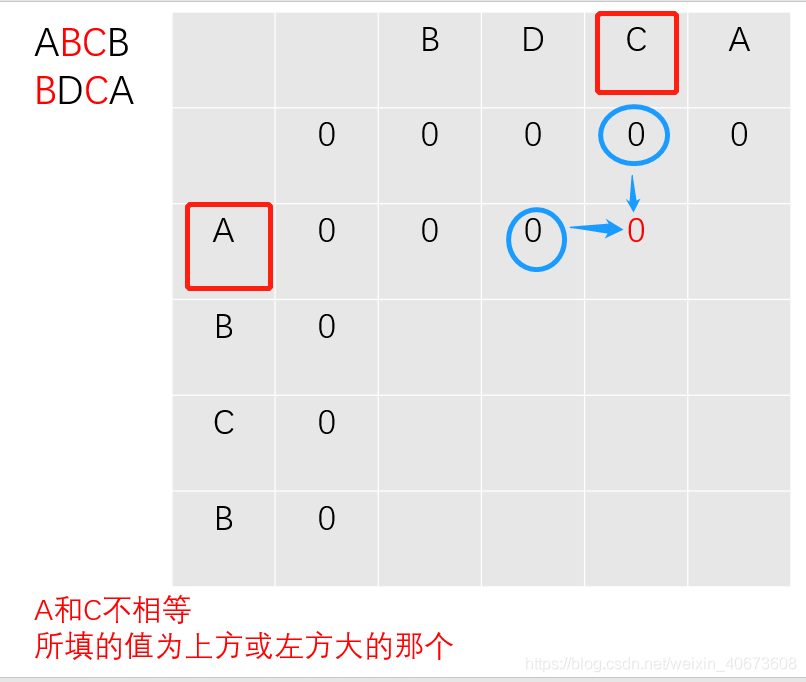
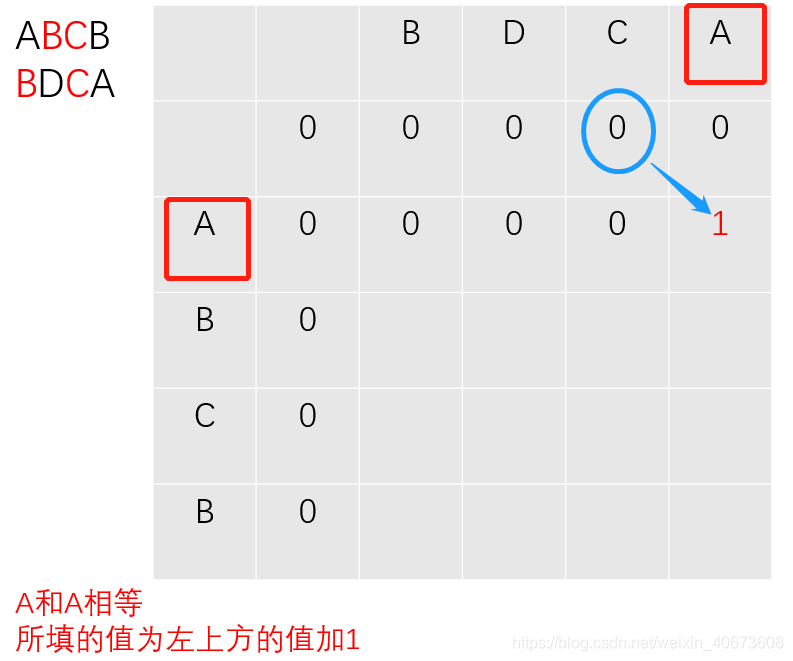
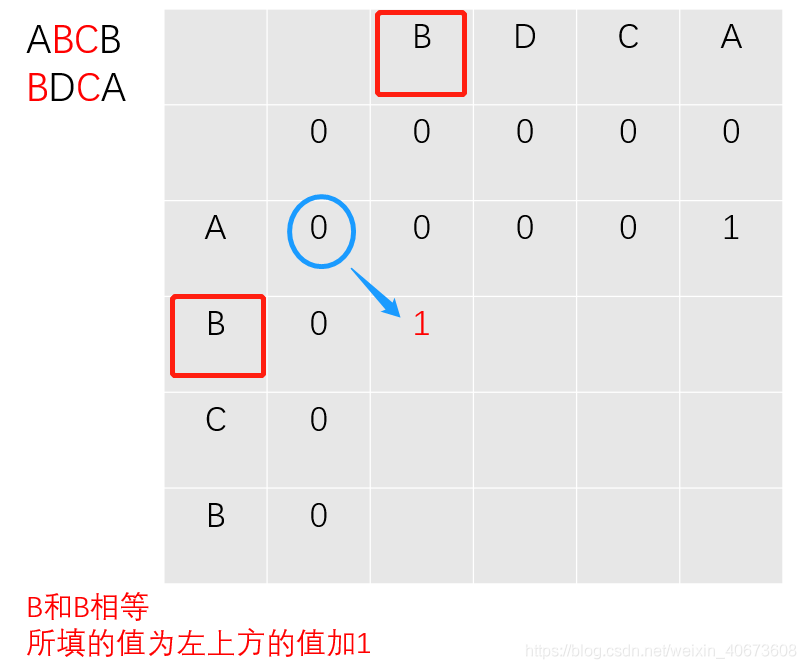
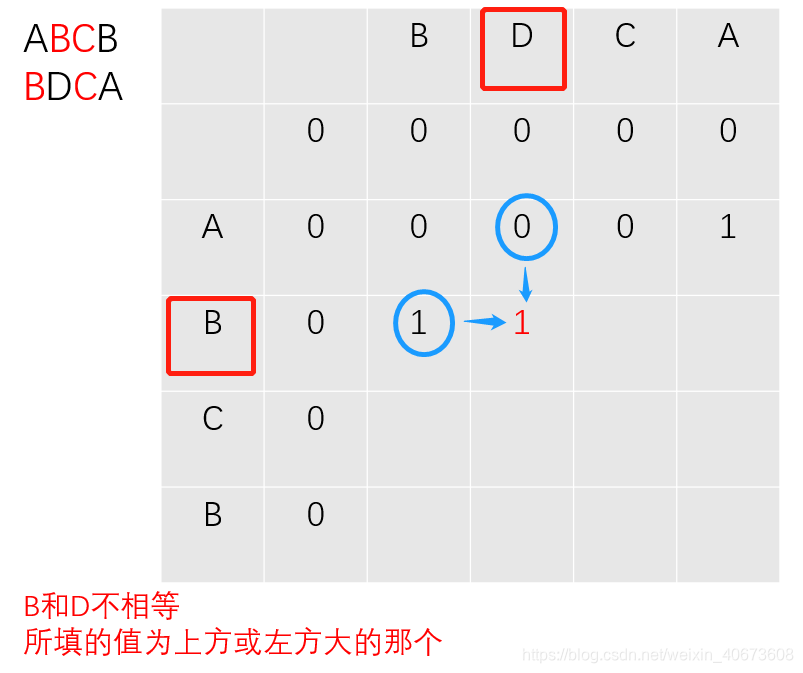
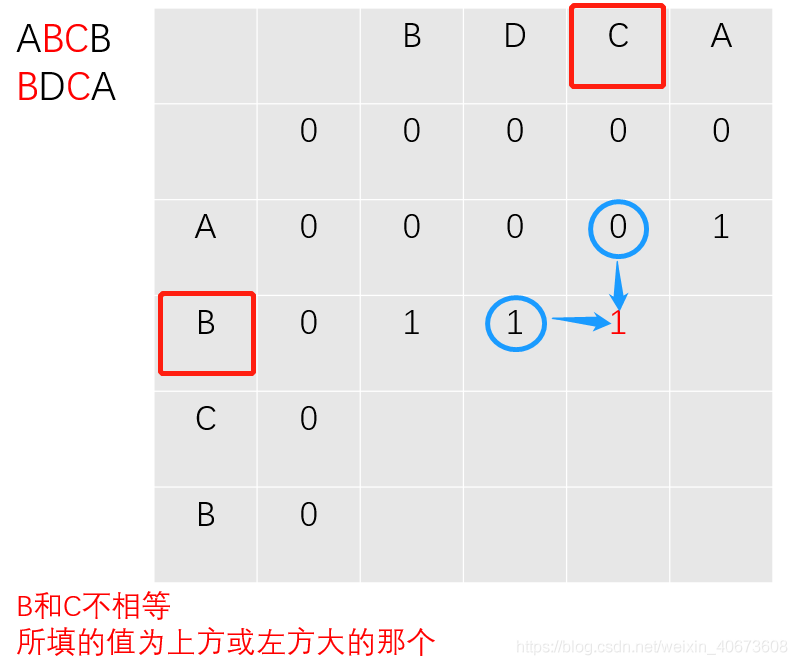
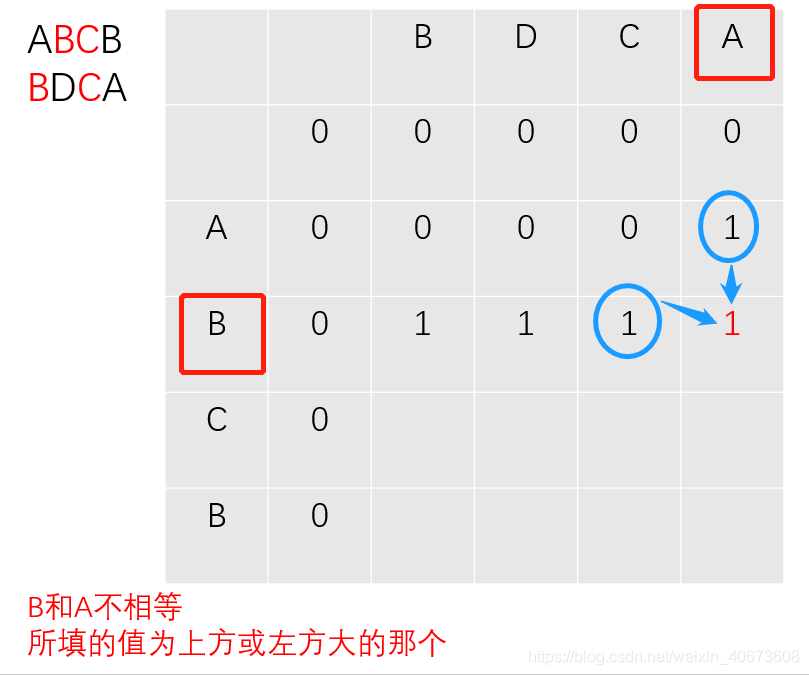
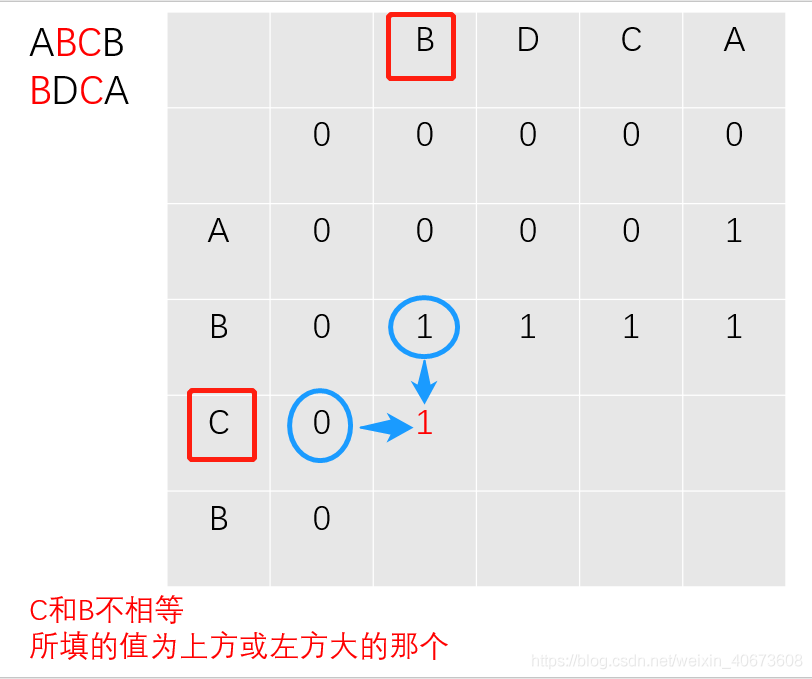
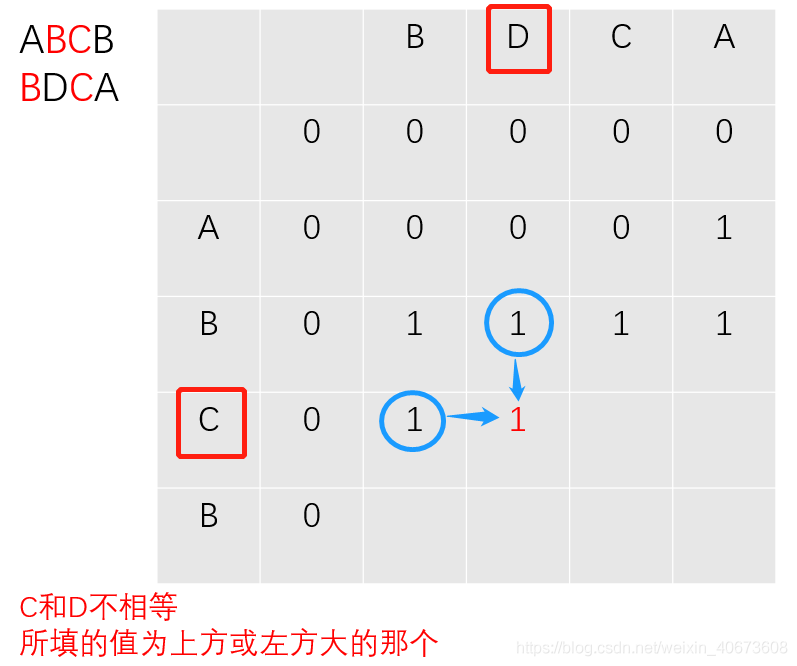
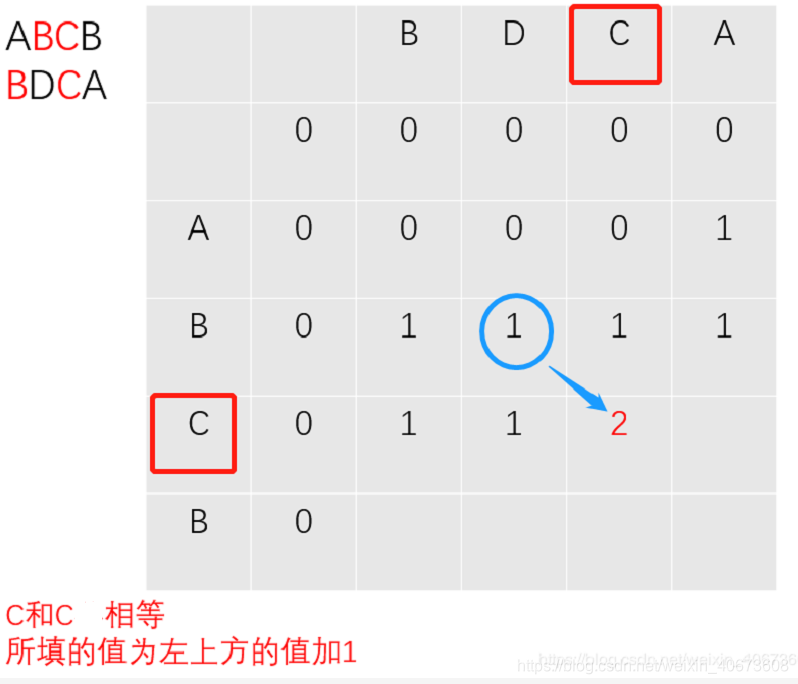
以此类推
最后填出的表为:
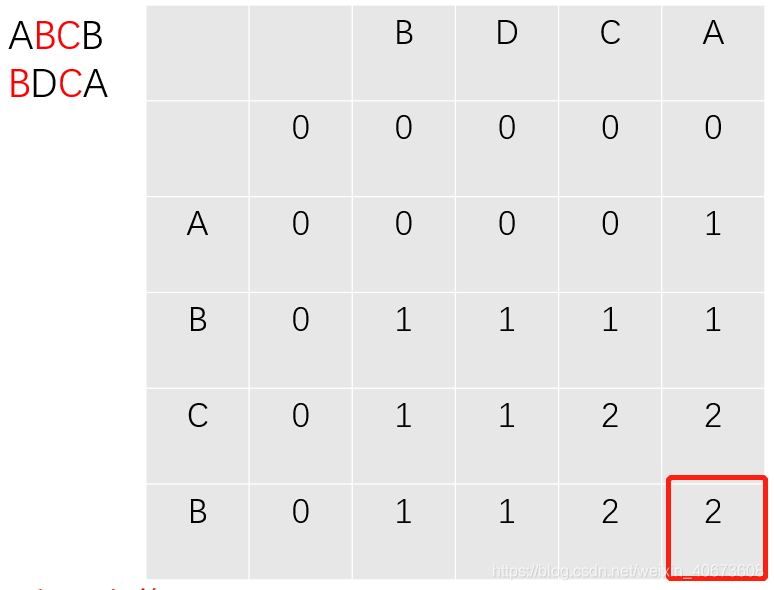
右下角的2即为LCS的长度
时间复杂度:
由于只需要填一个m行n列的二维数组,其中m代表第一个字符串长度,n代表第二个字符串长度
所以时间复杂度为O(m*n)
代码:
#include <iostream>
#include <string>
#include <stack>
using namespace std;
void LCS(string s1,string s2)
{int m=s1.length()+1;int n=s2.length()+1;int **c;int **b;c=new int* [m];b=new int* [m];for(int i=0;i<m;i++){c[i]=new int [n];b[i]=new int [n];for(int j=0;j<n;j++)b[i][j]=0;}for(int i=0;i<m;i++)c[i][0]=0;for(int i=0;i<n;i++)c[0][i]=0;for(int i=0;i<m-1;i++){for(int j=0;j<n-1;j++){if(s1[i]==s2[j]){c[i+1][j+1]=c[i][j]+1;b[i+1][j+1]=1; //1表示箭头为 左上}else if(c[i][j+1]>=c[i+1][j]){c[i+1][j+1]=c[i][j+1];b[i+1][j+1]=2; //2表示箭头向 上}else{c[i+1][j+1]=c[i+1][j];b[i+1][j+1]=3; //3表示箭头向 左}}}for(int i=0;i<m;i++) //输出c数组{for(int j=0;j<n;j++){cout<<c[i][j]<<' ';}cout<<endl;}stack<char> same; //存LCS字符stack<int> same1,same2; //存LCS字符在字符串1和字符串2中对应的下标,方便显示出来for(int i = m-1,j = n-1;i >= 0 && j >= 0; ){if(b[i][j] == 1){i--;j--;same.push(s1[i]);same1.push(i);same2.push(j);}else if(b[i][j] == 2)i--;elsej--;}cout<<s1<<endl; //输出字符串1for(int i=0;i<m && !same1.empty();i++) //输出字符串1的标记{if(i==same1.top()){cout<<1;same1.pop();}elsecout<<' ';}cout<<endl<<s2<<endl; //输出字符串2for(int i=0;i<n && !same2.empty();i++) //输出字符串2的标记{if(i==same2.top()){cout<<1;same2.pop();}elsecout<<' ';}cout<<endl<<"最长公共子序列为:";while(!same.empty()){cout<<same.top();same.pop();}cout<<endl<<"长度为:"<<c[m-1][n-1]<<endl;for (int i = 0; i<m; i++){delete [] c[i];delete [] b[i];}delete []c;delete []b;
}
int main()
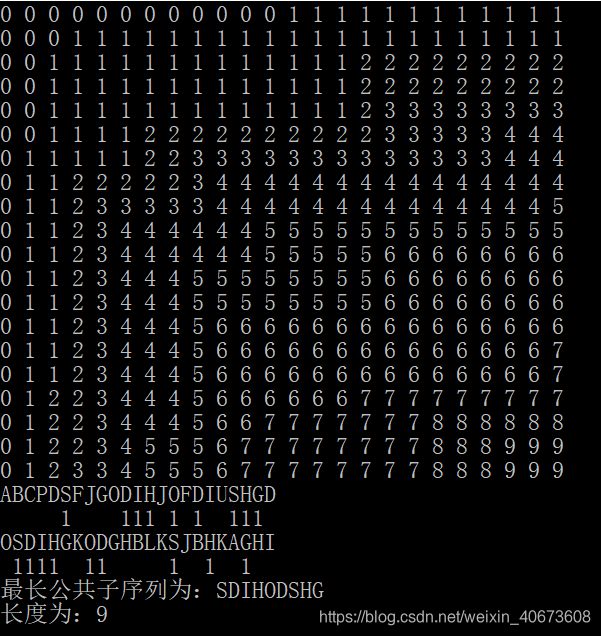
{string s1="ABCPDSFJGODIHJOFDIUSHGD";string s2="OSDIHGKODGHBLKSJBHKAGHI";LCS(s1,s2);return 0;
}
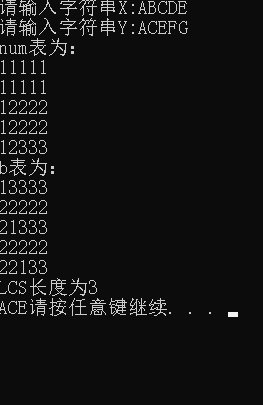
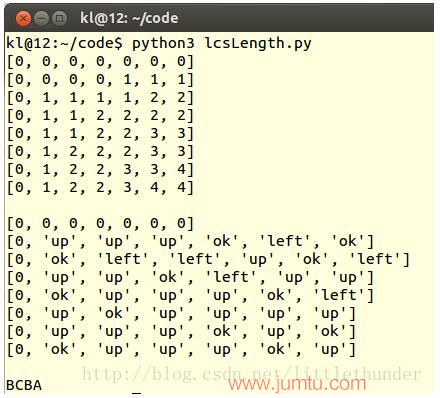
结果示例: