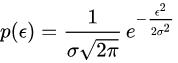自从2010年开始,不安全的直接对象引用(IDOR)就已经成为了OWASP Top 10 Web应用安全风险中影响程度排名第四的安全漏洞了。
IDOR将允许一名授权用户获取其他用户的信息,意指一个已经授权的用户通过更改访问时的一个参数,从而访问到了原本其并没有得到授权的对象。Web应用往往在生成Web页面或服务时会用它的真实名字,且并不会对所有目标对象的请求访问进行用户权限检测,所以这就造成了不安全的对象直接引用的漏洞。换句话说,不安全的直接对象引用漏洞将允许攻击者通过页面或服务向特殊对象资源发送访问请求,如果系统不会对请求发送者的身份权限进行合理认证的话,就说明这个系统中存在不安全的直接对象引用。
OWASP定义
不安全的直接对象引用允许攻击者绕过网站的身份验证机制,并通过修改指向对象链接中的参数值来直接访问目标对象资源,这类资源可以是属于其他用户的数据库条目以及服务器系统中的隐私文件等等。导致这种情况出现的原因是,系统在接受用户输入并利用输入信息获取对象之前没有对用户身份权限进行检测。
应用程序在SQL查询语句中直接使用了未经测试的数据,而攻击者可以利用这一点来访问数据库中的其他账号数据。
漏洞利用场景
我们假设下面这种场景:Web应用允许已登录用户修改自己的秘密值。首先,这个秘密值肯定是要跟用户在数据库中的账号绑定在一起的。当前用户“bee”已经登录了Web服务器,他可以随意修改他自己的秘密值,但他并不打算这样做。因为他准备做一次恶作剧,然后修改其他用户的秘密值。
不安全的直接对象引用漏洞入门指南
在BurpSuite的帮助下,我们捕获到了浏览器发送的请求。你可以从下图中看到,登录用户为bee,秘密值为hello。接下来,我们使用其他用户来修改这个用户的信息。
SQLquery = “SELECT * FROM useraccountsWHERE account = ‘bee’;
[外链图片转存失败(img-lmsoSx8Z-1567062948873)(https://image.3001.net/images/20170706/14993334728966.png)]
不安全的直接对象引用漏洞入门指南
接下来,我们准备将该用户的用户名修改为raj。想要在应用中执行这种攻击的话,则至少需要两个用户账号。
SQLquery = “SELECT * FROM useraccountsWHERE account = ‘raj’;
不安全的直接对象引用漏洞入门指南
非常好!!!我们成功地修改了用户raj的秘密值。请注意,如果攻击目标是任意一个官方网站,那么攻击者的目标肯定是管理员账号。
不安全的直接对象引用漏洞入门指南
场景二
接下来我们一起看看第二种漏洞利用场景,这跟绝大多数的IDOR攻击场景非常相似。
现在我们准备通过一个电影购票网站来在线订购电影票,示例网站地址为 bookmyshow.com,这个网站中存在不安全的直接对象引用漏洞。
在这个网站中,我打算订购十张电影票,每张票的加个为十五欧元。接下来,我们确认订单,然后使用BurpSuite来捕捉浏览器请求。
不安全的直接对象引用漏洞入门指南
捕获到的请求如下图所示,高亮部分包含了需要订购的电影票数量、每张票的价格(十五欧元)以及订单类型。接下来,我们就要尝试修改订单金额,将加个修改成我们想要的价格:
不安全的直接对象引用漏洞入门指南
我将单张票价修改为了一欧元,这也就意味着我只需要花十欧元就能买十张票了。下图中显示了请求信息:
不安全的直接对象引用漏洞入门指南
[外链图片转存失败(img-laLrtyf7-1567062911849)(https://image.3001.net/images/20170706/14993335431357.png)]
没错,我们成功地用十欧元购买了十张电影票!
总结
这篇文章只是一篇不安全的直接对象引用漏洞入门指南,这种漏洞的利用方式和利用场景还远远不止本文所描述的这么简单,感兴趣的用户可以自行动手搭建一个这样的测试环境,然后亲自尝试去利用这种漏洞,毕竟实践出真知嘛。有关此漏洞的其他信息,可参考OWASP给出的内容。