概念

最小二乘法是勒让德( A. M. Legendre)于1805年在其著作《计算慧星轨道的新方法》中提出的。最小二乘法就是通过最小化误差的平方和，使得拟合对象无限接近目标对象。在图像处理中主要用于拟合线，通过求采样点距离误差最小的线，可以是直线，曲线，椭圆，圆等。求解方法目前分为多项式和概率（最大似然）估计两种。

最小二乘法多项式拟合，根据给定的点，求出它的函数y=f(x)。
假设有点 , I = 1,2,3,……n,求近似曲线y=φ(x)，并且使得y=φ(x)与y=f(x)的平方偏差和最小。
最大似然估计方法是通过将真实值和测量值得误差形成一个概率分布函数P，联立后L（x），求x的偏导，得到一个正态分布函数。

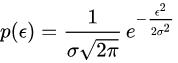
理论

最小二乘法小结

程序

使用opencv实现下：

int main()
{vector<Point> points;points.push_back(Point(25, 40));points.push_back(Point(7, 6));points.push_back(Point(11, 10));points.push_back(Point(12, 14));points.push_back(Point(35, 69));points.push_back(Point(30, 50));points.push_back(Point(43, 57));points.push_back(Point(25, 37));points.push_back(Point(27, 39));points.push_back(Point(50, 100));Mat src = Mat::zeros(200, 200, CV_8UC3);for (int i = 0; i < points.size(); i++){circle(src, points[i], 3, Scalar(0, 0, 255), 1, 8);}int N = 2;Mat A = Mat::zeros(N, N, CV_64FC1);for (int row = 0; row < A.rows; row++){for (int col = 0; col < A.cols; col++){for (int k = 0; k < points.size(); k++){A.at<double>(row, col) = A.at<double>(row, col) + pow(points[k].x, row + col);}}}//构建B矩阵Mat B = Mat::zeros(N, 1, CV_64FC1);for (int row = 0; row < B.rows; row++){for (int k = 0; k < points.size(); k++){B.at<double>(row, 0) = B.at<double>(row, 0) + pow(points[k].x, row) * points[k].y;}}Mat X;solve(A, B, X, DECOMP_LU);cout << X << endl;vector<Point>lines;for (int x = 0; x < src.size().width; x++){				// y = b + ax;double y = X.at<double>(0, 0) + X.at<double>(1, 0) * x;printf("(%d,%lf)\n", x, y);lines.push_back(Point(x, y));}polylines(src, lines, false, Scalar(255, 0, 0), 1, 8);imshow("拟合线", src);waitKey(0);return 0;
}

后面会再增加拟合圆的例子

参考文章：
如何理解最小二乘法？