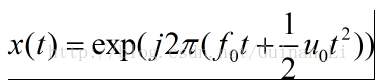线性调频信号（chirp信号）

顾名思义，该信号的频率随着时间线性变换，其复数表达形式如下：
$$s(t)=e^{2j\pi (f_{0}t+0.5\mu t^2)}$$
根据欧拉公式，其相位项为$2\pi (f_{0}t+0.5\mu t^2))$。信号的角频率是相位对时间的导数。对相位求导后有$2\pi (f_0+\mu t)$，显然，$f_0$表示线性调频起始频率，$\mu$表示调频斜率。

下面设一个线性调频信号，起始频率$f_0=24GHz$,调频带宽$B=10GHz$，采样频率为$f_s=240GHz$，采样时宽$T=100ns$，据此可以计算调频斜率为$\mu =B/T=10^{17}Hz/s$（注：参数仅供参考，并未考虑实际可行性）

对该信号添加一个信噪比为$5$dB的高斯白噪声，可以得到其时域图如下所示：

上方的图是前1e-9秒的信号，下放的图是最后1e-9秒的信号，可以看出信号变得“紧密”了一些，这是因为频率从$24GHz$线性上升到了$34GHz$。

利用fft观察双边频谱如下图

虽然噪声很大，但是也可以大致看出，在$24GHz$到$34GHz$的频带上幅度较高。
这张图还可以说明，一般的傅里叶变换对chirp信号的检测能力不足，噪声稍大一些就会淹没信号。下面利用分数阶傅里叶变换处理chirp信号。

分数阶傅里叶变换检测chirp信号

线性调频信号作为一种典型的非平稳信号，具有大时宽带宽积的特殊优势，广泛应用于雷达、通信、地质探测和声呐信号处理等研究领域。因此，研究线性调频信号具有十分重要的意义。分数阶傅里叶变换实质上是一种线性变换,它不仅可以理解为chirp基分解，还没有交叉干扰的问题。所以，分数阶傅里叶变换特别适合用来处理chirp类信号。[1]

我的理解：就像平面任意一个矢量可以分解为x,y两个基向量一样，任意一个线性调频信号也可以分解成两个chirp基。只要选择对了合适的阶数，分数阶傅里叶变换就可以在把这个chirp信号的能量集中在这个方向上的基向量上，形成一个冲激脉冲（易于检测），而一般的傅里叶变换通常并不在这个“最优方向”上，所以能量散开，具有了一定的带宽，不利于检测。
（以上想法仅供参考，不保证正确性）

分数阶傅里叶变换的原理及其快速算法（Ozakats算法）的MATLAB实现在我的另一篇博客中：分数阶傅里叶变换（FrFT）详细原理与matlab代码实现

下面从最基础的分数阶傅里叶变换公式入手[2]：

式中的$B_a(x,x^{\prime })$表示卷积核，$f(x)$表示信号，$x^{\prime }$表示与$x$不同的变量而不是导数。
将上述线性调频信号的公式代入，合并指数项，可以得到积分号里面的表达式为：
$$\begin{gathered} B_a(x,x^{\prime })f(x^{\prime })=A_{\varphi }\exp (i\pi (x^2\cot \varphi )-2x{x}^{\prime }\csc \varphi +x^{\prime 2}\cot \varphi )\cdot \exp (i\pi \mu x^{\prime 2}+2i\pi f_0{x}^{\prime }) \\ =A_{\varphi }\exp (i\pi (x^2\cot \varphi )+2x^{\prime }(f_0-x\csc \varphi )+x^{\prime 2}(\mu +\cot \varphi )) \end{gathered}$$
该积分是对$x^{\prime }$变量积分，于是着重观察含$x^{\prime }$的项，包括一次项$2x^{\prime }(f_0-x\csc \varphi )$和二次项$x^{\prime 2}(\mu +\cot \varphi )$.

调整阶数$a$，使得$\mu =-\cot \varphi$，消去二次项。

在没有二次项的条件下，再假设$x=f_0/\csc \varphi$，消去一次项，于是积分内部没有$x^{\prime }$，可以去掉积分号，变换结果为$A_{\varphi }\exp (i\pi x^2\cot \varphi )$，代入$x=f_0/\csc \varphi$，显然这是一个非零项。
如果$x\ne f_0/\csc \varphi$，就会出现一个一次项的积分。由于$\sin t$和$\cos t$的周期性，其无穷积分等于零，再根据欧拉公式，有下式成立:
$${\int }_{-\infty }^{\infty }{e}^{it}dt=0$$
因此一次项的存在会使整个积分为0，换句话说，该积分只有在$x=f_0/\csc \varphi$处有值，而在其它地方为0，类似于冲激函数。
在二次项存在的情况下，该积分就没有上述性质，能量散开，不易检测。

参考文献[1]总结了利用分数阶傅里叶变换检测chirp信号的步骤以及参数估计的公式：

其中${\alpha }_0$在上文中指$\varphi$。整个问题变成了一个二维最优化问题，优化目标是最大化分数阶傅里叶变换函数的值，参数为阶数$a$和频率$x$。

注意，在实际操作中发现上述参数估计方程并不正确。进一步查阅文献并参考了他人代码后发现，上述参数估计方程是适用于连续函数的，在实际的计算机中都是离散信号，因此${\mu }_0$需要使用归一化调频斜率$k=\frac{B}{f_s}$，且$x\csc \varphi$实际是中心频率而不是起始频率。

---

2022.10.3学习更新：
此处得出的确实是中心频率，原因是本文的信号是[0,T]范围内的，而上述推导过程包括参数归一化是在[-T/2,T/2]范围内的，当信号时间处于这个范围内，估计出来的频率确实是初始频率。
有前辈也有这个疑惑，参见matlab论坛https://www.ilovematlab.cn/thread-277599-1-1.html

---

仿真

在例如汽车防撞雷达等一些场景中，我们提前知道要检测的chirp信号参数，可以直接根据参数估计分数阶傅里叶分解的阶数，进而直接检测目标信号。
假设我们使用上文中的chirp参数，首先求解归一化调频斜率$k=\frac{B}{f_s}=0.0417$
代入参数估计公式中，计算旋转角度$\varphi =arccot(-k)=-1.5292$，然后计算阶次$a=\varphi /\frac{\pi }{2}=-0.9735$
负数不影响结果，实际上分数阶傅里叶变换周期为4，而对于chirp信号检测来说，$\cot (\varphi )=\cot (\varphi +\pi )，$周期进一步缩小为2。

对chirp信号做阶数为-0.9735的分数阶傅里叶变换，得到如下时频域图：

由图可以看出，信号在2.8976e10的位置出现了一个非常大的峰值，相比于fft的频域图像，显然这个峰值更容易检测到。因此使用分数阶傅里叶变换比一般的傅里叶变换更抗噪声干扰。

令$x=2.8976e10$，估计信号的中心频率为$x\csc \varphi =29Ghz$，因此可以推算出起始频率为24Ghz，与预设相符。

代码

close all
fs=24e10;%采样频率
T=1e-7;%时宽
B=10e9;%带宽
mu=B/T;%调频率
n=round(T*fs);%采样点个数
t=linspace(0,T,n);
f0=24e9;%起始频率
s=exp(2j*pi*(f0*t+0.5*mu*t.^2));
SNR=5;%信噪比
s=awgn(s,SNR);%添加一定信噪比的高斯白噪声figure
subplot(211)
plot(t,real(s))%时域图
title("调频信号时域")
xlabel("t/s")
xlim([0,1e-9])
grid onsubplot(212)
plot(t,real(s))%时域图
title("调频信号时域")
xlabel("t/s")
xlim([T-1e-9,T])
grid onfigure
S=fftshift(fft(real(s))./n);
f=linspace(-fs/2,fs/2-1,n);%频域横坐标，注意奈奎斯特采样定理，最大原信号最大频率不超过采样频率的一半
plot(f,abs(S))%频域图
title("发射信号频域")
xlim([-50e9,50e9])
grid onk=B/fs;%归一化调频斜率
a=acot(-k)/(pi/2);%以归一化调频斜率估计阶次
% a=pi/2+atan(n-1)*mu/fs^2;
% for a=0.9:0.01:1
figure
S=myfrft(real(s),a);
f=linspace(-fs/2,fs/2-1,n);%频域横坐标，注意奈奎斯特采样定理，最大原信号最大频率不超过采样频率的一半
plot(f,abs(S))%频域图
title("发射信号时频域")
% xlim([0,fs/2-1])
title("a="+num2str(a))
grid on
% endfh_=abs(f(abs(S)==max(abs(S)))*csc(a*pi/2));%估计的中心频率
f0_=fh-B/2;%估计的起始频率

参考文献

[1] 渠莹,杨俊. 基于分数阶傅里叶变换的LFM信号参数估计[J]. 物联网技术,2017,7(11):30-32. DOI:10.16667/j.issn.2095-1302.2017.11.006.
[2] OZAKTAS H.M., ARIKAN O… Digital computation of the fractional Fourier transform[J]. IEEE Transactions on Signal Processing: A publication of the IEEE Signal Processing Society,1996,44(9):2141-2150.

---

注：本人系初学者，以上仅为个人学习笔记，可能存在错误，有任何问题欢迎在评论区讨论。本文将会随着学习理解的加深而继续修改。