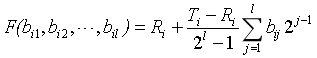在接触学习多目标优化的问题上,经常会被提及到多目标遗传算法NSGA-II,网上也看到了很多人对该算法的总结,但真正讲解明白的以及配套用算法实现的文章很少,这里也对该算法进行一次详解与总结。会有侧重点的阐述,不会针对NSGA以及算法复杂度等等进行,有相关需求可自行学习了解。文末附有Python与Matlab两种的源代码案例。
目录
1、什么是非支配遗传算法
2、支配与非支配关系
2.1、种群分层
2.2、如何进行分支配排序
3、拥挤度(密度评估)
4、快速非支配性排序方法
5、偏序关系
6、 什么是精英策略
7、NSGA-II算法的基本思想
8、Matlab非支配代码实现
9、Python代码完整版实现
10、算法改进策略说明
文末有彩蛋
在串讲算法原理之前,先说明几个关键词。
1、什么是非支配遗传算法
非支配排序遗传算法NSGA (Non-dominated Sorting Genetic Algorithms)是由Srinivas和Deb于1995年提出的。这是一种基于Pareto最优概念的遗传算法,它是众多的多目标优化遗传算法中体现Goldberg思想最直接的方法。该算法就是在基本遗传算法的基础上,对选择再生方法进行改进:将每个个体按照它们的支配与非支配关系进行分层,再做选择操作,从而使得该算法在多目标优化方面得到非常满意的结果。
2、支配与非支配关系
在最小化问题中,
理解起来就是,任意一个目标分量,的值都不大于
,并且在这些目标分量中至少存在一个目标分量
的值严格比
的值小,记作
.
2.1、种群分层
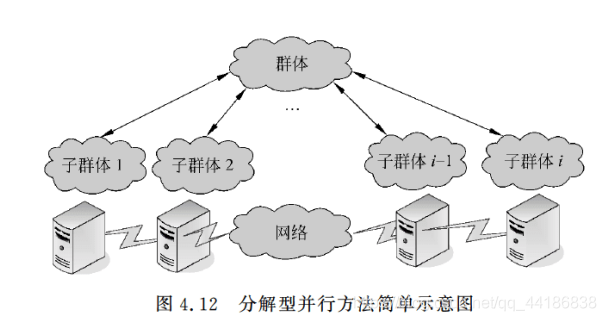
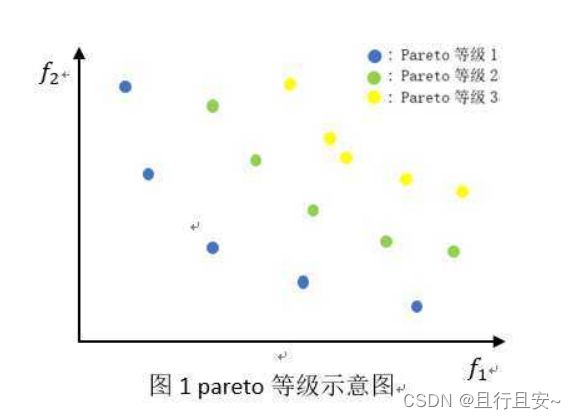
当出现大量满足支配与非支配的个体时,会出现一种如下的分层现象。因为优化问题,通常存在一个解集,这些解之间就全体目标函数而言是无法比较优劣的,其特点是:无法在改进任何目标函数的同时不削弱至少一个其他目标函数。
这种解称作非支配解(nondominated solutions)或Pareto最优解(Pareto optimal solutions),形象展示如下:
2.2、如何进行分支配排序
(1)设i=1;
(2)所有的且
,按照以上定义比较个体
和个体
之间的支配与非支配关系;
(3)如果不存在任何一个个体优于
,,则
标记为非支配个体
(4)令i=i+1,转到步骤(2),直到找到所有的非支配个体。
通过上述步骤得到的非支配个体集是种群的第一级非支配层,然后忽略这些已经标记的非支配个体(即这些个体不再进行下一轮比较),再遵循步骤(1)-(4),就会得到第二级非支配层。依此类推,直到整个种群被分层。
3、拥挤度(密度评估)
为了获得对种群中某一特定解附近的密度估计, 我们沿着对应目标计算这个解两侧的两点间的平均距离。 这个值是对用最近的邻居作为顶点形成的长方体的周长的估计(称之为拥挤距离)。在图 1 中, 第i 个解在其前沿的拥挤距离(用实心圆标记)是长方体的平均边长(用虚线框表示。(用实心圆标记的点是同一非支配前沿的解)

拥挤距离的计算需要根据每个目标函数值的大小对种群进行升序排序。此后,对于每个目标函数,边界解(对应函数最大最小值的解)被分配一个无穷距离值。所有中间的其他解被分配一个与两个相邻解的函数值的归一化差的绝对值相同的距离值。 对其他目标函数继续进行这种计算。总的拥挤距离值为对应于每个目标的各个距离之和。在计算拥挤距离之前, 归一化每个目标函数。 下面所示的算法概述了非支配性解集 中所有解的拥挤距离计算过程。对非支配性解集进行拥挤距离分配

这里, 是指集合中第
个个体的第
个目标函数值,参数
和
是第m 个目标函数的最大和最小值.
4、快速非支配性排序方法
对于每个个体 都设有以下两个参数
和
,
: 在种群中支配个体
的解个体的数量。
: 被个体
所支配的解个体的集合。
1)找到种群中所有 n(i)=0 的个体, 将它们存入当前集合F(1);
2)对于当前集合 F(1) 中的每个个体 , 考察它所支配的个体集
, 将集合
中的每个个体 k 的 n(k) 减去1, 即支配个体 k 的解个体数减1;( 对其他解除去被第一层支配的数量, 即减
1) 如 n(k)-1=0则将个体 k 存入另一个集H。
( 3) 将 F(1) 作为第一级非支配个体集合, 并赋予该集合内个体一个相同的非支配序 i(rank), 然后继续对 H 作上述分级操作并赋予相应的非支配序, 直到所有的个体都被分级。 其计算复杂度为,m为目标函数个数, N为种群大小。按照1 )、 2) 的方法完成所有分级,示意图如下。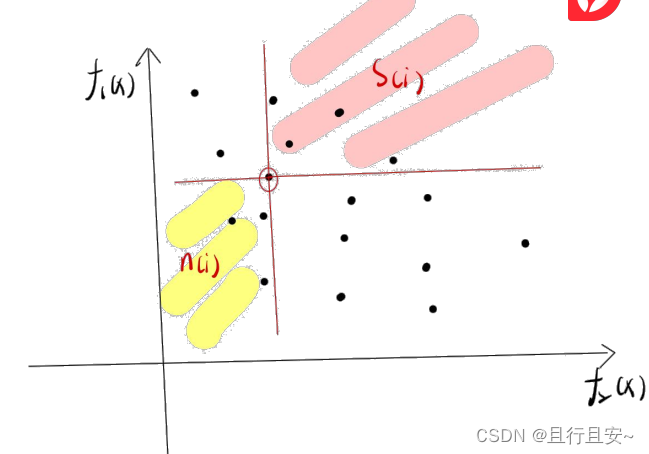
5、偏序关系
由于经过了排序和拥挤度的计算,群体中每个个体都得到两个属性:非支配序
和拥挤度
,则定义偏序关系为
:当满足条件
,或满足
且
时,定义
。也就是说:如果两个个体的非支配排序不同,取排序号较小的个体(分层排序时,先被分离出来的个体);如果两个个体在同一级,取周围较不拥挤的个体。
6、 什么是精英策略
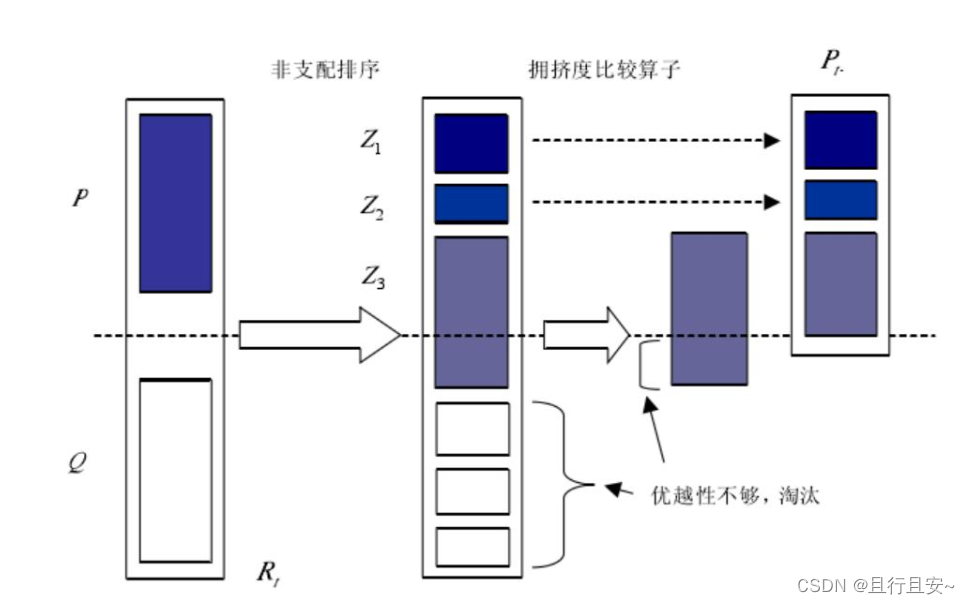
NSGA-II 算法采用精英策略防止优秀个体的流失, 通过将父代和子代所有个体混合后进行
非支配排序的方法。 精英策略的执行步骤:
7、NSGA-II算法的基本思想
1) 随机产生规模为N的初始种群Pt,经过非支配排序、 选择、 交叉和变异, 产生子
代种群Qt, 并将两个种群联合在一起形成大小为2N的种群Rt,;
2)进行快速非支配排序, 同时对每个非支配层中的个体进行拥挤度计算, 根据非支
配关系以及个体的拥挤度选取合适的个体组成新的父代种群Pt+1﹔
3) 通过遗传算法的基本操作产生新的子代种群Qt+1, 将Pt+1与Qt+1合并形成新的种
群Rt, 重复以上操作, 直到满足程序结束的条件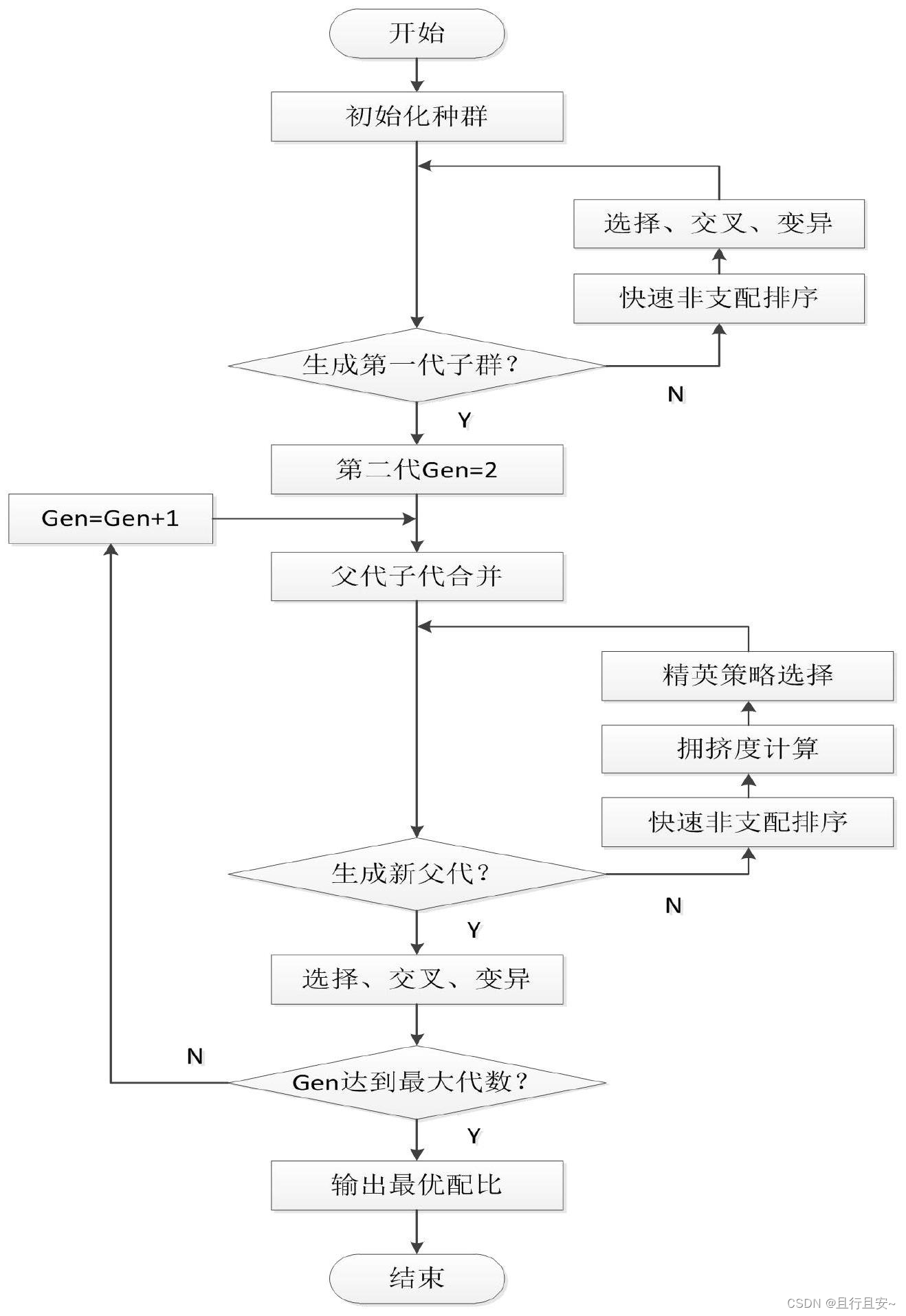
8、Matlab非支配代码实现
Matlab版本的数据案例(重点以拥挤度函数与非支配排序为主),网上案例很多都是使用matlab,请自行查阅学习。
function [FrontValue,MaxFront] = NonDominateSort(FunctionValue,Operation)
% 进行非支配排序
% 输入: FunctionValue, 待排序的种群(目标空间),的目标函数
% Operation, 可指定仅排序第一个面,排序前一半个体,或是排序所有的个体, 默认为排序所有的个体
% 输出: FrontValue, 排序后的每个个体所在的前沿面编号, 未排序的个体前沿面编号为inf
% MaxFront, 排序的最大前面编号if Operation == 1Kind = 2; elseKind = 1; %√end[N,M] = size(FunctionValue);MaxFront = 0;cz = zeros(1,N); %%记录个体是否已被分配编号FrontValue = zeros(1,N)+inf; %每个个体的前沿面编号[FunctionValue,Rank] = sortrows(FunctionValue);%sortrows:由小到大以行的方式进行排序,返回排序结果和检索到的数据(按相关度排序)在原始数据中的索引%开始迭代判断每个个体的前沿面,采用改进的deductive sort,Deb非支配排序算法while (Kind==1 && sum(cz)<N) || (Kind==2 && sum(cz)<N/2) || (Kind==3 && MaxFront<1)MaxFront = MaxFront+1;d = cz;for i = 1 : Nif ~d(i)for j = i+1 : Nif ~d(j)k = 1;for m = 2 : Mif FunctionValue(i,m) > FunctionValue(j,m) %比较函数值,判断个体的支配关系k = 0;break;endendif k == 1d(j) = 1;endendendFrontValue(Rank(i)) = MaxFront;cz(i) = 1;endendend
end%% 非支配排序伪代码
% def fast_nondominated_sort( P ):
% F = [ ]
% for p in P:
% Sp = [ ] #记录被个体p支配的个体
% np = 0 #支配个体p的个数
% for q in P:
% if p > q: #如果p支配q,把q添加到Sp列表中
% Sp.append( q ) #被个体p支配的个体
% else if p < q: #如果p被q支配,则把np加1
% np += 1 #支配个体p的个数
% if np == 0:
% p_rank = 1 #如果该个体的np为0,则该个体为Pareto第一级
% F1.append( p )
% F.append( F1 )
% i = 0
% while F[i]:
% Q = [ ]
% for p in F[i]:
% for q in Sp: #对所有在Sp集合中的个体进行排序
% nq -= 1
% if nq == 0: #如果该个体的支配个数为0,则该个体是非支配个体
% q_rank = i+2 #该个体Pareto级别为当前最高级别加1。此时i初始值为0,所以要加2
% Q.append( q )
% F.append( Q )
% i += 1function CrowdDistance = CrowdDistances(FunctionValue,FrontValue)
%分前沿面计算种群中每个个体的拥挤距离[N,M] = size(FunctionValue);CrowdDistance = zeros(1,N);Fronts = setdiff(unique(FrontValue),inf);for f = 1 : length(Fronts)Front = find(FrontValue==Fronts(f));Fmax = max(FunctionValue(Front,:),[],1);Fmin = min(FunctionValue(Front,:),[],1);for i = 1 : M[~,Rank] = sortrows(FunctionValue(Front,i));CrowdDistance(Front(Rank(1))) = inf;CrowdDistance(Front(Rank(end))) = inf;for j = 2 : length(Front)-1CrowdDistance(Front(Rank(j))) = CrowdDistance(Front(Rank(j)))+(FunctionValue(Front(Rank(j+1)),i)-FunctionValue(Front(Rank(j-1)),i))/(Fmax(i)-Fmin(i));endendend
end9、Python代码完整版实现
下面将给出Python版本的案例实现。
# Program Name: NSGA-II.py
# author;lxy
# Time:2023/03/11#Importing required modules
import math
import random
import matplotlib.pyplot as plt#First function to optimize
def function1(x):value = -x**2return value#Second function to optimize
def function2(x):value = -(x-2)**2return value#Function to find index of list,且是找到的第一个索引
def index_of(a,list):for i in range(0,len(list)):if list[i] == a:return ireturn -1#Function to sort by values 找出front中对应值的索引序列
def sort_by_values(list1, values):sorted_list = []while(len(sorted_list)!=len(list1)):if index_of(min(values),values) in list1:sorted_list.append(index_of(min(values),values))values[index_of(min(values),values)] = math.infreturn sorted_list#Function to carry out NSGA-II's fast non dominated sort
def fast_non_dominated_sort(values1, values2):S=[[] for i in range(0,len(values1))] #len(values1)个空列表front = [[]]n=[0 for i in range(0,len(values1))]rank = [0 for i in range(0, len(values1))]#将front0全部整理出来了,并未对front1-n等进行整理for p in range(0,len(values1)):S[p]=[]n[p]=0for q in range(0, len(values1)):if (values1[p] > values1[q] and values2[p] > values2[q]) or (values1[p] >= values1[q] and values2[p] > values2[q]) or (values1[p] > values1[q] and values2[p] >= values2[q]):if q not in S[p]:S[p].append(q)elif (values1[q] > values1[p] and values2[q] > values2[p]) or (values1[q] >= values1[p] and values2[q] > values2[p]) or (values1[q] > values1[p] and values2[q] >= values2[p]):n[p] = n[p] + 1if n[p]==0:rank[p] = 0if p not in front[0]:front[0].append(p)i = 0#该循环能将所有的个体全部进行分类,显然最后一层的个体中,没有可以支配的个体了while(front[i] != []):Q=[]for p in front[i]:for q in S[p]:n[q] =n[q] - 1if( n[q]==0):rank[q]=i+1if q not in Q:Q.append(q)i = i+1front.append(Q)del front[len(front)-1] #删除了最后一层无支配个体的front层,最后一层是空集return front#Function to calculate crowding distance 同层之间的一个计算
def crowding_distance(values1, values2, front):# distance = [0 for i in range(len(front))]lenth= len(front)for i in range(lenth):distance = [0 for i in range(lenth)]sorted1 = sort_by_values(front, values1[:]) #找到front中的个体索引序列sorted2 = sort_by_values(front, values2[:]) #找到front中的个体索引序列distance[0] = 4444distance[lenth-1] = 4444for k in range(2,lenth-1):distance[k] = distance[k]+ (values1[sorted1[k+1]] - values1[sorted1[k-1]])/(max(values1)-min(values1))# print("/n")print("k:",k)print("distance[{}]".format(k),distance[k])for k in range(2,lenth-1):distance[k] = distance[k]+ (values2[sorted2[k+1]] - values2[sorted2[k-1]])/(max(values2)-min(values2))return distance# #Function to carry out the crossover
def crossover(a,b):r=random.random()if r>0.5:return mutation((a+b)/2)else:return mutation((a-b)/2)# #Function to carry out the mutation operator
def mutation(solution):mutation_prob = random.random()if mutation_prob <1:solution = min_x+(max_x-min_x)*random.random()return solution#Main program starts here
pop_size = 10
max_gen = 100#Initialization
min_x=-55
max_x=55
solution=[min_x+(max_x-min_x)*random.random() for i in range(0,pop_size)]
print('solution',solution)
gen_no=0
while(gen_no<max_gen):print('\n')print('gen_no:迭代次数',gen_no)function1_values = [function1(solution[i])for i in range(0,pop_size)]function2_values = [function2(solution[i])for i in range(0,pop_size)]print('function1_values:',function1_values)print('function2_values:', function2_values)non_dominated_sorted_solution = fast_non_dominated_sort(function1_values[:],function2_values[:])print('front',non_dominated_sorted_solution)# print("The best front for Generation number ",gen_no, " is")# for valuez in non_dominated_sorted_solution[0]:# print("solution[valuez]",round(solution[valuez],3),end=" ")
# print("\n")crowding_distance_values=[]for i in range(0,len(non_dominated_sorted_solution)):crowding_distance_values.append(crowding_distance(function1_values[:],function2_values[:],non_dominated_sorted_solution[i][:]))print("crowding_distance_values",crowding_distance_values)solution2 = solution[:]#Generating offspringswhile(len(solution2)!=2*pop_size):a1 = random.randint(0,pop_size-1)b1 = random.randint(0,pop_size-1)solution2.append(crossover(solution[a1],solution[b1]))print('solution2',solution2)function1_values2 = [function1(solution2[i])for i in range(0,2*pop_size)]function2_values2 = [function2(solution2[i])for i in range(0,2*pop_size)]non_dominated_sorted_solution2 = fast_non_dominated_sort(function1_values2[:],function2_values2[:]) #2*pop_sizeprint('non_dominated_sorted_solution2', non_dominated_sorted_solution2)# print("\n")crowding_distance_values2=[]for i in range(0,len(non_dominated_sorted_solution2)):crowding_distance_values2.append(crowding_distance(function1_values2[:],function2_values2[:],non_dominated_sorted_solution2[i][:]))print('crowding_distance_values2',crowding_distance_values2)new_solution= []for i in range(0,len(non_dominated_sorted_solution2)):non_dominated_sorted_solution2_1 = [index_of(non_dominated_sorted_solution2[i][j],non_dominated_sorted_solution2[i] ) for j in range(0,len(non_dominated_sorted_solution2[i]))]print('non_dominated_sorted_solution2_1:',non_dominated_sorted_solution2_1)front22 = sort_by_values(non_dominated_sorted_solution2_1[:], crowding_distance_values2[i][:])print("front22",front22)front = [non_dominated_sorted_solution2[i][front22[j]] for j in range(0,len(non_dominated_sorted_solution2[i]))]print('front',front)front.reverse()for value in front:new_solution.append(value)if(len(new_solution)==pop_size):breakif (len(new_solution) == pop_size):breaksolution = [solution2[i] for i in new_solution]gen_no = gen_no + 1
#
# Lets plot the final front now
function1 = [i * -1 for i in function1_values]
function2 = [j * -1 for j in function2_values]
plt.xlabel('Function 1', fontsize=15)
plt.ylabel('Function 2', fontsize=15)
plt.scatter(function1, function2)
plt.show()
最终得出的Pareto前沿解的图像为:
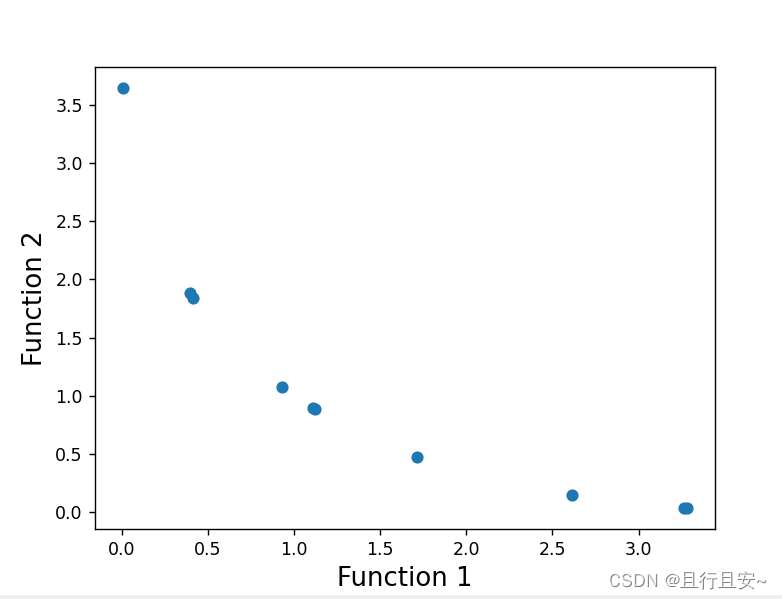
10、算法改进策略说明
算法改进部分,在文章的另一篇,请跳转观看。彩蛋加餐
多目标遗传算法NSGA-II改进策略
如还有其他问题,欢迎留言沟通。
后续应该会针对具体的现实问题如生产调度问题,车辆路径问题等进行算法实现。