遗传算法原理及其python实现

遗传算法原理

基本思想：

遗传算法（Genetic Algorithm，GA）是一种进化算法，其基本原理是仿效生物界中的“物竞天择、适者生存”的演化法则，它最初由美国Michigan大学的J. Holland教授于1967年提出。
遗传算法是从代表问题可能潜在的解集的一个种群（population）开始的，而一个种群则由经过基因（gene）编码的一定数目的个体(individual)组成。因此，第一步需要实现从表现型到基因型的映射即编码工作。初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代（generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度(fitness）大小选择个体，幵借助于自然遗传学的遗传算子（genetic operators）进行组合交叉和变异，产生出代表新的解集的种群。这个过程将导致种群像自然进化一样，后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。

基本概念
与进化论相似，遗传算法有几个核心概念。知道进化论或学过生物的很容易理解。

个体（Individual）：一个猴子，一个猩猩，一个人。
种群（Population）：一群猴子，一群猩猩，一群人。
基因（Gene）：个体携带的基因。
染色体（Chromosome）：由基因拼接组成；作为个体的蓝本，在算法中一般代表个体自身。

遗传算法有三个基本操作：选择（Selection）、交叉（Crossover）和变异（Mutation）。

选择选择的目的是为了从当前群体中选出优良的个体，使它们有机会作为父代为下一代繁衍子孙。根据各个个体的适应度值，按照一定的规则或方法从上一代群体中选择出一些优良的个体遗传到下一代种群中。选择的依据是适应性强的个体为下一代贡献一个或多个后代的概率大。选择的基准就是个体的适应度。而选择的策略根据问题和程序员自身意图，可以采用多种策略。一般使用较广、且易于实现的是轮盘赌策略（roulette wheel selection）。假设种群中有6个个体，适应度值分别是[2,3,10,5,12,19]，其轮盘是如下形式：

我们转动轮盘，显然适应度越大的有更大的概率被选中。其简单的解释性代码可以表示如下：轮盘赌也有一定的限制。如果适应度值有正有负，就不好处理。所以轮盘赌只是选择策略的一种。最简单的是随机选择策略，在种群中随机选择个体进行进化。

# -*- coding: utf-8 -*-
import numpy as np
s = [2, 3, 10, 5, 12, 19] # 种群和个体
s_sum = sum(s) # 所有适应度的和
m = 0
r = np.random.random() # 0-1之间的随机数
c = 0
for i in range(len(s)):m += s[i] / s_sumif r <= m:c = ibreak
print(c) # 最后选中个体的序号

交叉。通过交叉操作可以得到新一代个体，新个体组合了父辈个体的特性。将群体中的各个个体随机搭配成对，对每一个个体，以交叉概率交换它们之间的部分染色体。两个个体parent1和parent2，各分成2部分基因片段。分别将parent1的前部分基因片段和parent2的后部分基因片段，parent1的后部分基因片段和parent2的前部分基因片段相结合，生成了2个后代child1和child2。每个后代都拥有parent1和parent2的一部分基因。在每一代进化中，交叉过程不是一定发生的，一般基于设定的概率发生。而这个概率设定的较高，一般在0.6以上。如果交叉不发生，parent1和parent2直接复制进入新种群。如果交叉发生，则对child1，child2，parent1，parent2进行适应度比较后，保留较好的进入新种群，也可以都进入新种群，具体怎么做没有标准，可以根据具体问题自行选择。

变异。对种群中的每一个个体，以变异概率改变某一个或多个基因座上的基因值为其他的等位基因。同生物界中一样，变异发生的概率很低，变异为新个体的产生提供了机会。

基本步骤

原理python实现

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt# 适应度函数,求取最大值
def fitness(x):return x + 16 * np.sin(5 * x) + 10 * np.cos(4 * x)# 个体类
class indivdual:def __init__(self):self.x = 0  # 染色体编码self.fitness = 0  # 个体适应度值def __eq__(self, other):self.x = other.xself.fitness = other.fitness# 初始化种群
#pop为种群适应度存储数组，N为个体数
def initPopulation(pop, N):for i in range(N):ind = indivdual()#个体初始化ind.x = np.random.uniform(-10, 10)#  个体编码。-10,10的正态分布，可以自己设定限定边界ind.fitness = fitness(ind.x)#计算个体适应度函数值pop.append(ind)#将个体适应度函数值添加进种群适应度数组pop# 选择过程
def selection(N):# 种群中随机选择2个个体进行变异（这里没有用轮盘赌，直接用的随机选择）return np.random.choice(N, 2)# 结合/交叉过程
def crossover(parent1, parent2):child1, child2 = indivdual(), indivdual()#父亲，母亲初始化child1.x = 0.9 * parent1.x + 0.1 * parent2.x #交叉0.9,0.1，可以设置其他系数child2.x = 0.1 * parent1.x + 0.9 * parent2.xchild1.fitness = fitness(child1.x)#子1适应度函数值child2.fitness = fitness(child2.x)#子2适应度函数值return child1, child2
# 变异过程
def mutation(pop):# 种群中随机选择一个进行变异ind = np.random.choice(pop)# 用随机赋值的方式进行变异ind.x = np.random.uniform(-10, 10)ind.fitness = fitness(ind.x)# 最终执行
def implement():# 种群中个体数量N = 40# 种群POP = []# 迭代次数iter_N = 400# 初始化种群initPopulation(POP, N)# 进化过程for it in range(iter_N):#遍历每一代a, b = selection(N)#随机选择两个个体if np.random.random() < 0.65:  # 以0.65的概率进行交叉结合child1, child2 = crossover(POP[a], POP[b])new = sorted([POP[a], POP[b], child1, child2], key=lambda ind: ind.fitness, reverse=True)#将父母亲和子代进行比较，保留最好的两个POP[a], POP[b] = new[0], new[1]if np.random.random() < 0.1:  # 以0.1的概率进行变异mutation(POP)POP.sort(key=lambda ind: ind.fitness, reverse=True)return POPif __name__ =='__main__':pop = implement()# 绘图代码def func(x):return x + 16 * np.sin(5 * x) + 10 * np.cos(4 * x)x = np.linspace(-10, 10, 100000)y = func(x)scatter_x = np.array([ind.x for ind in pop])scatter_y = np.array([ind.fitness for ind in pop])best=sorted(pop,key=lambda pop:pop.fitness,reverse=True)[0]#最佳点print('best_x',best.x)print('best_y',best.fitness)plt.plot(x, y)#plt.scatter(scatter_x, scatter_y, c='r')plt.scatter(best.x,best.fitness,c='g',label='best point')plt.legend()plt.show()

参考文献
https://blog.csdn.net/saltriver/article/details/63679701

遗传算法工具箱

python也有诸如遗传算法/粒子群算法等启发式算法工具包，链接如下：

GitHub链接
scikit-opt是一个封装了7种启发式算法的 Python 代码库（差分进化算法、遗传算法、粒子群算法、模拟退火算法、蚁群算法、鱼群算法、免疫优化算法）

中文文档

import numpy as np
import matplotlib.pyplot as plt# 适应度函数,求取最大值
#因为GA函数是求最小值，所以我在适应度函数上加一个负号
#GA要求输入维度2维及其以上，所以我传入2个参数，第二维x2不用
def fitness(x):x1, x2 = x#x1=xreturn -(x1 + 16 * np.sin(5 * x1) + 10 * np.cos(4 * x1))# 个体类
from sko.GA import GAga = GA(func=fitness, n_dim=2, size_pop=50, max_iter=800, lb=[-10,0], ub=[10,0],precision=1e-7)
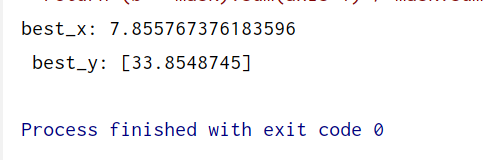
best_x, best_y = ga.run()
print('best_x:', best_x[0], '\n', 'best_y:', -best_y)def func(x):return x + 16 * np.sin(5 * x) + 10 * np.cos(4 * x)x = np.linspace(-10, 10, 100000)
y = func(x)plt.plot(x, y)
plt.scatter(best_x[0], -best_y, c='r',label='best point')plt.legend()
plt.show()