下面介绍的回归树和另一篇文章介绍的分类树，都属于决策树范畴。分类树的模型是每个非叶子节点都是一个分类特征，按照该分类特征的不同取值，将数据集分为多少个子集；并且分类树模型我们要找的是测试数据集的最终分类结果，而这个结果是标称型数据。而在回归树的概念中，每个非叶子节点也是需要根据某个特征分出子树，但是这个特征的取值是连续的，就不可能像分类树那样依据多少个取值分为多少个子树，所以在回归树模型中，一般都是二叉树，每个非叶子节点的分类特征都取一个值，小于这个值的数据分到左子树，大于这个值的分到右子树，等于这个值的我感觉是两边都可。
换一种说法，二叉树内部取“是”和“否”的分法，一个节点的条件时x<=a（a是我们计算出来的合适的分隔数据点），其中小于等于a的我们取“是”，也就是放到左子树，大于a的，我们取“否”，放到右子树。
- 回归树的生成
我们知道，不管是在回归树的生成过程中，还是生成之后，所有的叶子节点都是一堆数据集，而我们的目标就是对叶子节点上的数据集进行误差最小化分析，不断划分，直到叶子节点的误差小于一定的阈值。所以在每个叶子节点上，我们用平方误差
，来表示回归树训练过程中的预测误差，其中f(xi)是期望最优值，我们取所有yi的平均值，即
。下来就是需要取，最优的分割特征及其分割值，我们采用启发式方法（我理解的启发式方法，通俗的说，就是每次拿一个特征，然后取此特征按照一定步长改变该特征的值从小到大去试，然后遍历完所有特征后，取到误差最小的特征及其分割值）。下面先给出公式，然后对这个公式做解释：
上面的两个公式是对数据集进行预划分，R1和R2分别是划分后的两个数据集，j是选择第j个变量，也就是我们熟悉的第j个特征，s是划分标准，x(j)是每个样本中第j个变量的取值。上面已经将数据预划分成了两个数据集，下面就是要计算这两个数据集的误差：
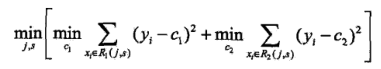
上式中的中括号里面的表示，在父节点划分标准为第j个变量，划分点为s的情况下，取两个子集小误差，里面是两个最小值的和，分别表示取一个合适的c1和c2，使子集的平方和最小，而这个c1和c2的取值分别是子集yi的平均数。而外层的循环，就是取合适的变量j，以及其合适的划分标准s使划分后的子集误差最小。
所以以上过程是个不断迭代的过程，不断取j和其对应的s值，等取完所有的j和s后，得到误差最小的那个j和s，作为此次的划分依据。
- 模型树的生成
其实模型树和回归树生成过程差不多，只不过是叶子结点的损失计算方式不同。从上面的回归树的生成过程可知，构建过程中每个叶子结点的预测值是yi的平均值，然后再用取平方误差的方式。但是模型树构建过程中，不用平均值作为预测值，而是用节点的样本拟合一条直线
，然后计算
作为预测值，放到回归树的生成过程中，f(xi)就是所有yi的平均值。
具体的直线拟合的公式，可以参考我的另一篇文章《回归》中拟合直线的方式。这里只给出计算公式：
是直线的拟合参数，X是样本数据，y是样本数据对应的结果。
- 决策树的剪枝
其实回归树和模型树的剪枝过程和分类树的剪枝过程类似，其损失函数都可以写成以下的表达式：
，和分类树不同的是预测误差的计算方式不同，即C(T)的计算方式不同。
，这里f(xi)是预测值或者平均数。
不过有的书上损失的函数的损失函数的计算方法没有考虑数的复杂程度，也就是没有α|T|项，这个应该是不同的书上有不同的方法，得知道有这么种方法。
