基于特征脸的人脸识别算法概述
—— 才疏学浅, 难免有错误和遗漏, 欢迎补充和勘误.
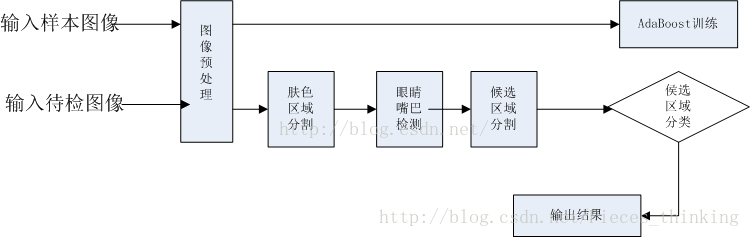
特征脸识别算法(EigenFaceRecognizer)是一种在主成分分析(PCA)中进行人脸辨识的技术。基于特征脸的驾驶人身份识别流程图为:

-
采集驾驶人图像作为训练样本
令驾驶人保持常用的驾驶坐姿,采集期间目视前方,将采集到的图像作为训练样本数据。 -
处理训练数据:
假设采集到 M M M张人脸图像信息,把每张图像拉成一列(假设图片像素个数是 N N N),将这些向量放在一个矩阵 S S S中作为训练样本: S = [ Γ 1 , Γ 2 , … , Γ M ] S=\left[\begin{array}{llll}\Gamma_{1}, & \Gamma_{2}, & \ldots, & \Gamma_{M}\end{array}\right] S=[Γ1,Γ2,…,ΓM]

- 计算平均脸:
- 将S里值累加并取均值: ψ = 1 M ∑ i = 1 M Γ i \psi = \frac{1}{M}\sum\limits_{i = 1}^M {\Gamma i} ψ=M1i=1∑MΓi
- 然后将每个人脸图像 Γ i \Gamma i Γi都减去该均值 Ψ \Psi Ψ,使均值为0: Φ i = Γ i − Ψ ; i = 1 , 2 , ⋯ , M \Phi i = \Gamma i - \Psi ;i = 1,2, \cdots ,M Φi=Γi−Ψ;i=1,2,⋯,M
- 重新排列构成新的矩阵 T T T: T = [ Φ 1 , Φ 2 , ⋯ , Φ M ] T=\left[\begin{array}{llll}\Phi_{1}, & \Phi_{2}, & \cdots, & \Phi_{M}\end{array}\right] T=[Φ1,Φ2,⋯,ΦM]
-
PCA降维求协方差矩阵C:
C = 1 M T T T C = \frac{1}{M}{T^T}T C=M1TTT -
计算特征脸的特征向量:
- 求出协方差矩阵 C C C的特征向量 e i e_i ei,记这些协方差矩阵 C C C的特征向量为:
E = ( e 1 , e 2 , e 3 , ⋯ , e m ) E=\left(\begin{array}{lllll}e_{1}, & e_{2}, & e_{3}, & \cdots, & e_{\mathrm{m}}\end{array}\right) E=(e1,e2,e3,⋯,em) - 计算各个特征脸的特征向量为:
u i = ∑ i = 1 M e i k Φ k , i = 1 , 2 , ⋯ , M u_i = \sum\limits_{i = 1}^M e_{ik}\Phi_k,i = 1,2, \cdots ,M ui=i=1∑MeikΦk,i=1,2,⋯,M
- 人脸识别:
- 得到特征脸的特征向量 u i u_i ui后,再对样本中的每张图片进行权重的标识: ω i = u i ( Γ − Ψ ) , i = 1 , 2 , ⋯ , M \omega_i = u_i(\Gamma - \Psi ),i = 1,2, \cdots ,M ωi=ui(Γ−Ψ),i=1,2,⋯,M
- 把这些权重写成一个向量表示: Ω T = [ ω 1 , ω 2 , ⋯ , ω M ] \Omega^{T}=\left[\begin{array}{llll}\omega_{1}, & \omega_{2}, & \cdots, & \omega_{M}\end{array}\right] ΩT=[ω1,ω2,⋯,ωM]
- 将待检测的人脸图像 Γ \Gamma Γ输入后做主成分分析后,求 Ω \Omega Ω和 Ω k \Omega_k Ωk的欧氏距离得到: ε k = ∥ Ω − Ω k ∥ 2 \varepsilon_k = {\left\| {\Omega - \Omega_k} \right\|^2} εk=∥Ω−Ωk∥2
- 其中 Ω \Omega Ω表示待检测人脸图像的权重, Ω k \Omega_k Ωk表示训练集中某个人脸的权重,当 ε k \varepsilon_k εk小于设定的阈值时,则认定正在检测的人脸与样本中对应人脸是同一人的。