算法分析与设计 二分查找

二分查找的基本概念

​ 二分查找是一种在有序数组中查找某一特定元素的查找算法。这种查找方法将查找的时间复杂度从原本的线性时间提升到了对数时间范围，大大缩短了搜索时间。

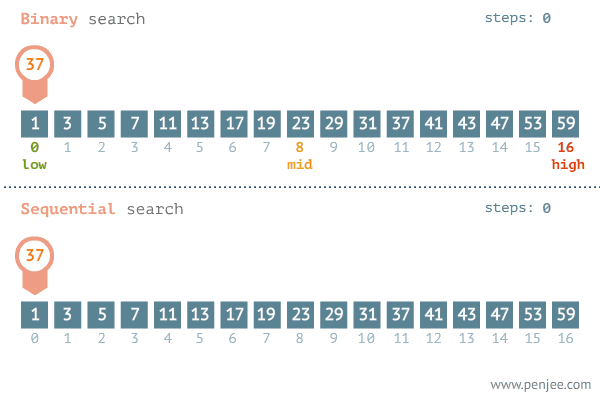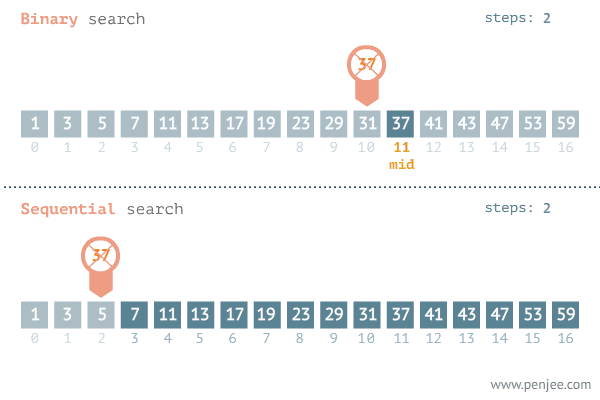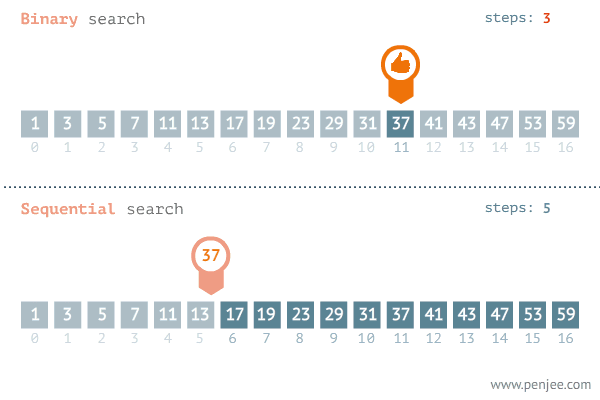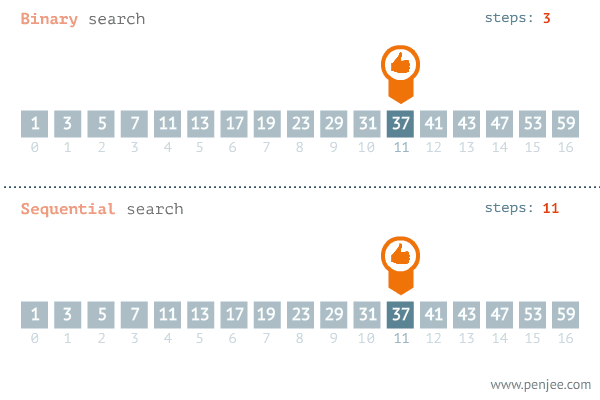
​ 二分查找的基本思想是：在查找过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则查找过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。

​ 一个基本的二分查找示例如下，在如下数组中找出元素4所在的位置：

int basicBinarySearch(vector<int> arr, int target){int left = 0;int right = arr.size() - 1;while(left <= right){int mid = left + (right-left)/2;if(target == arr[mid]){return mid;}else if (target < arr[mid]){right = mid - 1; }else if(target > arr[mid]){left = mid + 1;}}return -1;
}

​ 二分查找很简单，但是也有它的难点，其难点就在于在判定条件和边界值的选择上，很容易就会导致越界或者死循环的情况。

​ 对于循环的判定条件，如果查找区间是闭区间[left, right]，则判定条件要设为while(left<=right)，该判定条件是在出现left > right的情况下终止循环；如果这种闭区间查找区间下使用while(left < right)作为判定条件，该判定条件是在出现left >= right的情况下终止循环，这种情况就没有查找left == right是对应数组位置上的元素，导致错误的查找结果。如果查找区间是闭区间[left, right)，则判定条件可以设为while(left < right)。

​ 对于边界值，例如有序数组array = [1,2,4,4,4,4,5,6], target = 4，存在目标值有多个的情况，此时我们希望得到上边界目标值的索引，即为 5；或者希望得到下边界目标值的索引，即为 2。这时就不能找到目标值就返回，而是需要继续收紧边界进一步查找边界值。

int lowerBound(vector<int> arr, int target){int left = 0;int right = arr.size();int pos = -1;while(left < right){int mid = left + (right-left)/2;if(target == arr[mid]){pos = mid;right = mid;}else if(target < arr[mid]){right = mid;}else if(target > arr[mid]){left = mid + 1;}}return pos;
}int upperBound(vector<int> arr, int target){int left = 0;int right = arr.size();int pos = -1;while (left < right){int mid = left + (right-left)/2;if(target == arr[mid]){pos = mid;left = mid + 1;}else if(target < arr[mid]){right = mid;}else if(target > arr[mid]){left = mid + 1;}}return pos;
}

二分法求方程的根

​ 求方程$f(x)=x^3-5x^2+10x-80=0$ 的一个根，若求出的根是 $a$ ，则要求 $|f(a)|<=10^{-6}$

分析问题：

​ 对 $f(x)$ 求导得到，$f^{{}^{\prime }}(x)=3x^2-10x+10$ 。由一元二次方程求根公式知方程 $f^{{}^{\prime }}(x)=0$ 无解，所以 $f^{’}(x) $ 恒大于 0，可以得出该函数是单调递增的。另外计算可得 $f(0)<0,f(100)>0$ 所以在区间 [0,100] 内必然有且只有一个根，又该函数在该区间内是单调递增的，所以可以使用二分法在该区间内寻找方程的根。

double equationRoot(double lower, double upper){double EPS = 1e-6;while(lower <= upper){double root = lower + (upper-lower)/2;double f_root = f(root);if(fabs(f_root) < EPS){return root;}else if(f_root > 0){upper = root;}else if(f_root < 0){lower = root;}}return 0;
}

寻找指定和的整数对

​ 输入 n, ( n<= 100,000) 个整数， 找出其中的两个数，它们之和等于整数 m ( 假定一定有解)。

分析问题：

​ 一种简单的思路是使用两重循环，枚举所有的取数方法，但是这种方式的时间复杂度是 $O(n^2)$，有没有更高效的算法呢？

​ 可以采用二分法，第一步：将输入的数组排序；第二步：对数组中的每个元素 i使用二分查找在数组中查找值为 m-i 的元素，其时间复杂度为 $O(nlog(n))$。

​ 当然本题也可以采用双指针的解法，第一步：将输入的数组排序；第二步：定义两个指针分别指向数组的头部和尾部，然后计算arr[head]+arr[tail]的值，如果该值大于 m，则让tail--，如果小于m，则让head++，直到找出和为m的整数对，双指针查找的时间复杂度为 $O(n)$。

// 二分查找解法
int integerToBinarySearch(vector<int> arr, int sum, vector<int>& res){sort(arr.begin(),arr.end());vector<int>::const_iterator cit;for(cit = arr.begin(); cit!=arr.end(); ++cit){int target = *cit;int left = 0;int right = arr.size() - 1;while (left <= right){int mid = left + (right-left)/2;if(target == (sum-arr[mid])){res.push_back(target);res.push_back(arr[mid]);return 1;}else if (target > (sum-arr[mid])){right = mid - 1;}else if (target < (sum-arr[mid])){left = mid + 1;}}}return 0;
}// 双指针解法
int integerPairTwoPointer(vector<int> arr, int sum, vector<int>& res){sort(arr.begin(),arr.end());int head = 0;int tail = arr.size()-1;while(head <= tail){if(arr[head]+arr[tail] == sum){res.push_back(arr[head]);res.push_back(arr[tail]);return 1;}else if(arr[head]+arr[tail] < sum){head++;}else if(arr[head]+arr[tail] > sum){tail--;}}return 0;
}

农夫和奶牛问题

​ 农夫 John 建造了一个有 N, (2<=N<=100,000) 个隔间的牛棚，这些隔间分布在一条直线上，坐标是x1,...,xN-1 (0<=xi<=1,000,000,000)。他的 C, (2<=C<=N) 头牛不满于隔间的位置分布，它们为牛棚里其他的牛的存在而愤怒。为了防止牛之间的互相打斗，他想把这些牛安置在指定的隔间，所有牛中相邻两头的最近距离越大越好。那么，这个最大的最近距离是多少呢？

分析问题：

​ 牛棚的隔间要从第一个开始，我们直接把room设为1，因为第一次判断位置可用的话就是两个房间，后面可用的房间每次增加一，更新坐标是当判断当前房间可用的时候，此时判断下一个房间是否可用，并且更新当前位置，最后跟C比较，看房间是否够用。

​ 抽象为二分查找的方法，第一步：先将隔间的坐标 x1,...,xN-1 排序；第二步在区间 [left, right]内用二分法尝试最大最近距离 $D=(left+right)/2$ ，left 和 right 的初始值分别为 0 和 1,000,000,000/C。在第二部中如果D可行，则记住该D并在新的区间[left=D+1, right]中继续尝试新的D；如果D不可行，则在新的区间[left, right=D-1]中继续搜索合适的D。

bool isValid(int D, int C) {int room = 1, loc = 0;for (int i=1; i<n; i++) {if (pos[i] - pos[loc] >= D) {room++;loc = i;}}if (room >= C) return true;else return false;
}int FarmerAndCow(vector<int> arr, int C){sort(arr.begin(),arr.end());int left = 1, right = arr.size()-1;while (left <= right) {int mid = left + (left-right)/2;if (isValid(mid)) {left = mid + 1;return mid;} else {right = mid - 1;}}return 0;
}

参考资料

程序设计与算法（二）算法基础

二分查找的写法