二分

有单调性一定可以二分，可以二分不一定有单调性
二分的本质是边界不是单调性(单调一定可以二分，不单调的有的也可以二分)

本质：在一个区间上，找到某种性质，每次可以将区间一分为二（存在边界），一个区间满足、另外一个区间不满足，答案就在边界上！

整数二分的两种情况：

在这里插入图片描述
两种模板的答案分别对应红、绿边界点(图上箭头所示)

一般步骤(简略版)：
1.确定一个区间，使得目标值一定在区间中。
2.找一个性质，满足：
(1)性质具有二段性(即可以分为两个区间)
(2)答案是二段性的分界点
最终结果：
循环结束后,l=r,答案就是上图我们所画的边界。
总结：
根据某个性质将目标值转化为二段性上的分界点(分界点就是答案)，具体来讲就是根据某个性质，这个性质使区间具有二段性，使答案在分界点上。

模板一：

bool check(int x) {/* ... */} // 检查x是否满足某种性质// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{while (l < r){int mid = l + r >> 1;if (check(mid)) r = mid;    // check()判断mid是否满足性质else l = mid + 1;}return l;
}

解释：
模板一对应上图绿色线段边界，属于>=target的第一个元素

模板二：

bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{while (l < r){int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}return l;
}

解释：
模板一对应上图红色线段边界，属于<=target的最后一个元素

总结：

在这里插入图片描述

lower_bound寻找>=x的第一个数，应该说lower_bound对应二分第一个模板,以此类推。
两个模板的区别就在于如何划分区间，以及mid的运算是否需要+1。

特别注意：
如果查的数没有，则模板一会找到比target大的第一个数，模板二会找比target小的最后一个数。

整数二分详细步骤：

找一个区间[L,R],使得答案一定在该区间中;
找一个判断条件，使得该判断条件具有二段性，并且答案一定是该二段性的分界点;
分析中点mid在该判断条件下是否成立，如果成立，考虑答案在哪个区间;如果不成立，考虑答案在哪个区间;
如果更新方式写的是r=mid,则不用做任何处理;如果更新方式写的是l=mid,则需要在计算mid时加上1(否则会造成死循环);

分析算法

说明：
我们根据某种性质，将目标值转化为相关边界点（红或绿的其中一个）,此时根据二段性，区间已经分成两个不同的区间，一个满足性质，另外一个不满足性质，且一般边界点在满足性质的区间上。
在这里插入图片描述
对于绿线段情况(前提条件：答案在绿线段分界点，箭头所指位置，左端点)，这里我们假设checked函数返回true时在答案所在段

如果checked(mid) 为 true（即满足某种性质）,即mid所在位置为绿线段内(因为根据二段性，此时区间已经分为红线段和绿线段两个区间),则答案(ans)一定在[L,M] 之间(因为需要让ans在绿线段边界,左端点)M也可能为答案，否则在 [M+1,R]之间，如果为true，在绿线段之间，则下次循环r=mid,否则l=mid+1,以此类推。

对于红线段情况((前提条件：答案在红线段右端点，箭头所指位置)，这里我们假设checked函数返回true时在答案所在段

如果checked(mid) 为 true（即满足某种性质）,即mid所在位置为红线段内(因为根据二段性，此时区间已经分为红线段和绿线段两个区间),则答案(ans)一定在[M,R] 之间(因为需要让ans在红线段边界,右端点)M也可能为答案，否则在 [L,M-1]之间，如果为true，在绿线段之间，则下次循环l=mid,否则r=mid-1,以此类推。(注意此时算mid时需要额外+1防止死循环！)。

上述如果、否则对应代码中if、else。

例题1：

给定一个按照升序排列的长度为 n 的整数数组，以及 q 个查询。

对于每个查询，返回一个元素 k 的起始位置和终止位置（位置从 0 开始计数）。

如果数组中不存在该元素，则返回-1 -1。

输入格式
第一行包含整数 n 和 q，表示数组长度和询问个数。

第二行包含 n 个整数（均在 1∼10000 范围内），表示完整数组。

接下来 q 行，每行包含一个整数 k，表示一个询问元素。

输出格式
共 q 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回-1 -1。

数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000
输入样例：

6 3
1 2 2 3 3 4
3
4
5

输出样例：

3 4
5 5
-1 -1

时/空限制：1s / 64MB
来源：AcWing


#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 100010;int n, m;
int q[N];int main()
{scanf("%d%d", &n, &m);for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);for (int i = 0; i < m; i ++ ){int x;scanf("%d", &x);// 二分x的左端点,绿线段情况int l = 0, r = n - 1;   // 确定区间范围while (l < r){int mid = l + r >> 1;if (q[mid] >= x) r = mid;//q[mid]>=x即为性质，将区间一分为二，将目标值转化为分界点，因为只有含目标值的区间满足此性质，不含目标值的区间不满足此性质，且满足此性质的区间分界点就是我们的答案！else l = mid + 1;}if (q[r] == x){cout << r << ' ';// 二分x的右端点r = n - 1;  // 右端点一定在[左端点, n - 1] 之间while (l < r){int mid = l + r + 1 >> 1;   // 因为写的是l = mid，所以需要补上1if (q[mid] <= x) l = mid;else r = mid - 1;}cout << r << endl;}else cout << "-1 -1" << endl;}return 0;
}

例题2：（没有单调性的二分说明）

不修改数组找出重复的数字

给定一个长度为 n+1 的数组nums，数组中所有的数均在 1∼n 的范围内，其中 n≥1。

请找出数组中任意一个重复的数，但不能修改输入的数组。

样例
给定 nums = [2, 3, 5, 4, 3, 2, 6, 7]。

返回 2 或 3。

思考题：如果只能使用 O(1) 的额外空间，该怎么做呢？

class Solution {
public:int duplicateInArray(vector<int>& nums) {int l=1,r=nums.size()-1;//此时的区间是1-n的数，不是nums数组！while(l<r){int mid=(l+r)/2;int cnt=0;for(int i=0;i<nums.size()-1;i++){if(nums[i]<=mid)  cnt++;}if(cnt>mid) r=mid;#说明前半个区间中有重复的else l=mid+1;}return l;}};

解析：
(分治，抽屉原理) O(nlogn)O(nlogn)
这道题目主要应用了抽屉原理和分治的思想。

抽屉原理：n+1 个苹果放在 n 个抽屉里，那么至少有一个抽屉中会放两个苹果。

用在这个题目中就是，一共有 n+1 个数，每个数的取值范围是1到n，所以至少会有一个数出现两次。

然后我们采用分治的思想，将每个数的取值的区间[1, n]划分成[1, n/2]和[n/2+1, n]两个子区间，然后分别统计两个区间中数的个数。
注意这里的区间是指数的取值范围，而不是数组下标。

划分之后，左右两个区间里一定至少存在一个区间，区间中数的个数大于区间长度。
这个可以用反证法来说明：如果两个区间中数的个数都小于等于区间长度，那么整个区间中数的个数就小于等于n，和有n+1个数矛盾。

因此我们可以把问题划归到左右两个子区间中的一个，而且由于区间中数的个数大于区间长度，根据抽屉原理，在这个子区间中一定存在某个数出现了两次。

依次类推，每次我们可以把区间长度缩小一半，直到区间长度为1时，我们就找到了答案。

浮点数二分（只有一种情况）

模板如下：

bool check(double x) {/* ... */} // 检查x是否满足某种性质double bsearch_3(double l, double r)
{const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求while (r - l > eps){double mid = (l + r) / 2;if (check(mid)) r = mid;else l = mid;}return l;
}

例题：
给定一个浮点数 n，求它的三次方根。

输入格式
共一行，包含一个浮点数 n。

输出格式
共一行，包含一个浮点数，表示问题的解。

注意，结果保留 6 位小数。

数据范围
−10000≤n≤10000
输入样例：

1000.00

输出样例：

10.000000

代码：

#include <iostream>
#include <algorithm>using namespace std;int main()
{double x;cin >> x;double l = -10000, r = 10000;while (r - l > 1e-8)#一般比题目要求精度再往后两位，更保险{double mid = (l + r) / 2;if (mid * mid * mid >= x) r = mid;else l = mid;}printf("%lf\n", l);return 0;
}

总结

在这里我们举个例子：
我们需要查找下图红色字体6的位置，也就是值为6的第一个数，及>=target(6)的第一个数，我们就可以使用二分算法。
在这里插入图片描述
为什么可以使用二分？因为具有二段性,A段的值都小于6，B段的值都>=6,且答案就在B段的边界上

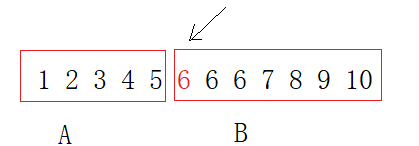
上图情况对应本文二分的第一个模板
如何写算法呢？
此时我们已经找到了某种性质(具体就是>=6的在一个段，<6的在一个段(每一个段中的所有数据都满足此段的性质)，不具体的就是>=target的数据在一个段,<target的数据在一个段)，可以将该区间分为二段，checked函数的书写就是根据性质来定的，但是checked函数必须满足其中一个段的性质(比如此题中性质分别是>=6、<6,那么checked函数需要是其中一个)，比如>=target返回true，或者<target返回true。
因为性质可以将区间分成两段，checked函数需要满足其中一段的性质，所以checked有两种写法，对应的if和else语句就有两种写法(其实就是两种情况的if和else语句内容交换了而已)。
过程：
1.根据任务(查找>=target的第一个数)确定性质(A段都<target,B段都>=target)，将区间分成两段，且目标值就是其中一段的边界点(易知在B段的边界点上)
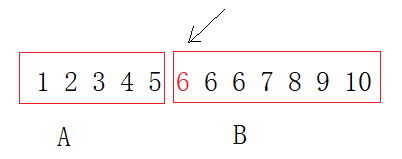
在这里插入图片描述
2.由上图可以确定使用的二分模板为模板一
3.checked函数
4.套用模板一
代码举例：
1.当checked函数返回true的性质在B段时

#include<iostream>
#include<vector>
using namespace std;
bool checked(int x){if(x>=6) return true;else return false;
}
int main()
{vector<int> v={1,2,3,4,5,6,6,6,7,8,9,10};int l=0,r=v.size()-1;while(l<r){int mid=(l + r) >> 1;//根据本次checked代码可以看出，当checked函数返回true时，说明在B段(答案所在的段)//为了使范围进一步缩小且越来越接近答案(B段边界点)，需要使r=midif(checked(v[mid])) r=mid;else l = mid+1;}cout<<l;return 0;
}

2.当checked函数返回true的性质在A段(非答案所在段)时

#include<iostream>
#include<vector>
using namespace std;
bool checked(int x){if(x<6) return true;else return false;
}
int main()
{vector<int> v={1,2,3,4,5,6,6,6,7,8,9,10};int l=0,r=v.size()-1;while(l<r){int mid=(l + r) >> 1;//根据本次checked代码可以看出，当checked函数返回true时，说明在A段(非答案所在段)//为了使范围进一步缩小且越来越接近答案(B段边界点)，需要使l=mid+1if(checked(v[mid])) l = mid+1;else r=mid;}cout<<l;return 0;
}

顺序：
1.找到一个性质将区间分成两段，此时根据性质已经可以确定答案在哪个段上的分界点了。换句话说就是我们根据想找的答案来确定某种性质，从而使其满足二分的要求，同时也确定了答案的位置(某一段的边界点)，在写代码前就已经确定了。
2.选择对应的二分模板，写checked函数，根据checked函数的书写不同，会有两种情况，每种情况if和else的代码也不同，两种情况无非就是if和else代码互换一下。
3.注意选择的模板在计算mid时是否需要额外+1.

举第二个例子：

我们需要查找下图红色字体6的位置，也就是值为6的最后一个数，及<=target(6)的最后一个数，我们就可以使用二分算法。
在这里插入图片描述
A段都<=6（性质），B段都>6（性质），我们根据这两个性质将区间分成了两段A段和B段，且答案就在A段的边界点(写代码前就已经判断出了答案在A段的边界点)
对应本文模板二

写代码：
1.checked(check)函数满足A段(<=6)时返回true

#include<iostream>
#include<vector>
using namespace std;
bool checked(int x){if(x<=6) return true;else return false;
}
int main()
{vector<int> v={1,2,3,4,5,6,6,6,7,8,9,10};int l=0,r=v.size()-1;while(l<r){int mid=(l + r + 1) >> 1;//根据本次checked代码可以看出，当checked函数返回true时，说明在A段(答案所在段)//为了使范围进一步缩小且越来越接近答案(A段分界点)，需要使l=mid,否则r=mid-1;if(checked(v[mid])) l = mid;else r=mid-1;}cout<<l;return 0;
}

2.checked(check)函数满足B段(>6)时返回true

#include<iostream>
#include<vector>
using namespace std;
bool checked(int x){if(x>6) return true;else return false;
}
int main()
{vector<int> v={1,2,3,4,5,6,6,6,7,8,9,10};int l=0,r=v.size()-1;while(l<r){int mid=(l + r + 1) >> 1;//根据本次checked代码可以看出，当checked函数返回true时，说明在B段(非答案所在段)//为了使范围进一步缩小且越来越接近答案(A段分界点)，需要使r=mid-1,否则l=mid;if(checked(v[mid])) r=mid-1;else l=mid;}cout<<l;//退出条件就是l=r,所以此时输出l和r都可以return 0;
}