01拉普拉斯变换定义
1.变换公式


2. 常见函数的Laplace变换


02 Laplace数值逆变换
根据拉普拉斯逆变换的公式,可以看到,f(t)可以变成如下的公式。

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# TEST1.PY -- by Dr. ZhuoQing 2020-07-10
#
# Note:
#============================================================from headm import *#################################################################
# Function InvLap(t,omega,sigma,nint), numerically inverts a #
# Laplace transform F(s) into f(t) using the Fast Fourier #
# Transform (FFT) algorithm for a specific time "t", an #
# upper frequency limit "omega", a real parameter "sigma" #
# and the number of integration intervals "nint" . #
# #
# Function F(s) is defined in separate as Fs(s) (see code #
# below). Fs(s) has to be changed accordingly everytime the #
# user wants to invert a different function. #
# #
# I suggest to use omega>100 and nint=50*omega. The higher #
# the values for omega, the more accurate the results will be #
# in general, but at the expense of longer processing times. #
# #
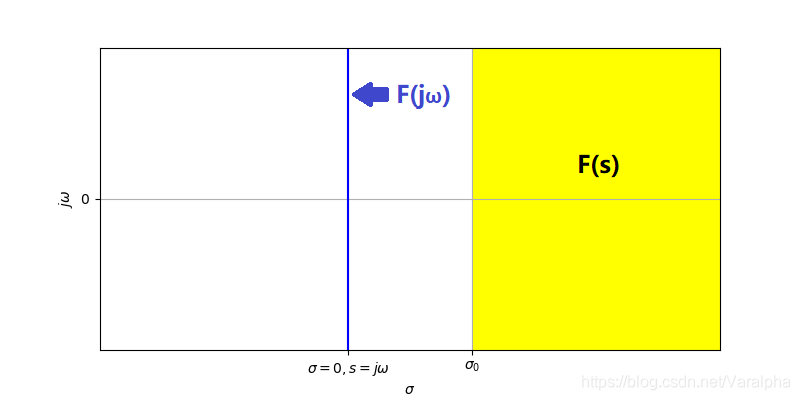
# Sigma is a real number which must be a little bigger than #
# the real part of rightmost pole of the function F(s). For #
# example, F(s) = 1/s + 1/(s-2) + 1/(s+1) has poles for s=0, #
# s=2 and s=-1. Hence, sigma must be made equal to, say, #
# 2.05 so as to keep all poles at the left of this value. #
# The analytical inverse for this simple function is #
# f(t) = 1 + exp(-t) + exp(2t). For t=1.25, omega=200, #
# nint=10000 and sigma=2.05, the numerical inversion yields #
# f(1.25) ~= 13.456844516, or -0.09% away from the actual #
# analytical result, 13.468998757 (results truncated to 9 #
# decimal places). This is the example used in this code. #
# #
# Creator: Fausto Arinos de Almeida Barbuto (Calgary, Canada) #
# Date: May 18, 2002 #
# E-mail: fausto_barbuto@yahoo.ca #
# #
# Reference: #
# Huddleston, T. and Byrne, P: "Numerical Inversion of #
# Laplace Transforms", University of South Alabama, April #
# 1999 (found at http://www.eng.usouthal.edu/huddleston/ #
# SoftwareSupport/Download/Inversion99.doc) #
# #
# Usage: invoke InvLap(t,omega,sigma,nint), for t>0. #
# #
#################################################################
# We need cmath because F(s) is a function operating on the
# complex argument s = a + bj
from math import ceil
from cmath import *# *** Driver InvLap function ***
def InvLap(t,omega,sigma,nint):
# Sanity check on some parameters.omega = ceil(omega)nint = ceil(nint)if omega <= 0:omega = 200if nint <= 0:nint = 10000return (trapezoid(t,omega,sigma,nint))# *** Function trapezoid computes the numerical inversion. ***
def trapezoid(t,omega,sigma,nint):sum = 0.0delta = float(omega)/nintwi = 0.0# The for-loop below computes the FFT Inversion Algorithm.
# It is in fact the trapezoidal rule for numerical integration.for i in range(1,(nint+1)):witi = complex(0,wi*t)wf = wi + deltawfti = complex(0,wf*t)fi = (exp(witi)*Fs(complex(sigma,wi))).realff = (exp(wfti)*Fs(complex(sigma,wf))).realsum = sum + 0.5*(wf-wi)*(fi+ff)wi = wfreturn ((sum*exp(sigma*t)/pi).real)# *** The Laplace function F(s) is defined here. ***
def Fs(s):
# return (1.0/s + 1.0/(s+1.0) + 1.0/(s-2.0))return 1.0/s# Function InvLap(t,omega,sigma,nint) is invoked.
printf(InvLap(1.25, 200, 3.05, 10000))#------------------------------------------------------------
# END OF FILE : TEST1.PY
#============================================================
03一些常见函数数值逆变换结果
- f(t)=sin(t)

def Fs(s):return 1/(s*s+1)

▲ sin(t)数值逆变换结果
-
f(t)=t


▲ 函数t的Laplace数值逆变换结果 -
f(t)=exp(-t)


▲ exp(-t)函数数值逆变换结果
※ 结论
本文测试了 一个简易版本的数值Laplace逆变换的程序。
这个算法需要人工给出积分的上下限,积分限的实部等。如果参数给定不合适,计算出来的数值误差较大。

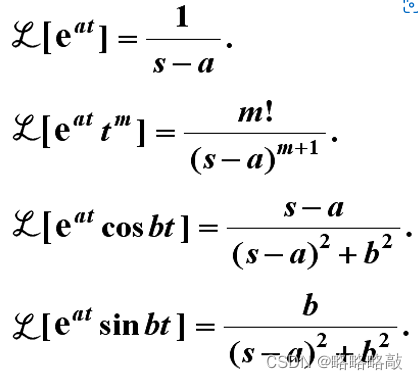


![[Matlab-5]Laplace变换](https://img-blog.csdnimg.cn/20210528100015487.png)