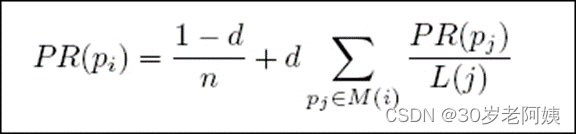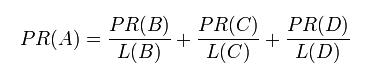数据挖掘十大算法:PageRank算法原理及实现

一、PageRank的概念

PageRank，网页排名，是一种由根据网页之间相互的超链接计算的技术，而作为网页排名的要素之一，它由Larry Page 和 Sergey Brin在20世纪90年代后期发明，并以拉里·佩吉（Larry Page）之姓来命名。

PageRank是Google专有的算法，用于衡量特定网页相对于搜索引擎索引中的其他网页而言的重要程度。PageRank算法计算每一个网页的PageRank值，然后根据这个值的大小对网页的重要性进行排序。该算法可以用于对网页进行排序，当然，也可以用于排序科技文章或社交网络中有影响的用户等。

二、算法原理

PageRank让链接来"投票" 。

一个页面的“得票数”由所有链向它的页面的重要性来决定，到一个页面的超链接相当于对该页投一票。一个页面的PageRank是由所有链向它的页面（“链入页面”）的重要性经过递归算法得到的。一个有较多链入的页面会有较高的等级，相反如果一个页面没有任何链入页面，那么它没有等级。

假设一个由4个页面组成的小团体：A，B，C和D。如果所有页面（B，C，D）都链向A：

那么A的PR（PageRank）值将是B，C及D的Pagerank总和：

继续假设B也有链接到D，并且D也有链接到包括A的3个页面（A，B，C）。

一个页面不能投票2次。所以B给每个页面半票。以同样的逻辑，D投出的票只有1/3算到了A的PageRank上：

换句话说，根据链出总数平分一个页面的PR值：

最后，所有这些被换算为一个百分比再乘上一个系数。由于“没有向外链接的页面”传递出去的PageRank会是0，所以，Google通过数学系统给了每个页面一个最小值：

说明：在Sergey Brin和Larry Page的1998年原文中给每一个页面设定的最小值是1-d，而不是这里的(1-d)/N。所以一个页面的PageRank是由其他页面的PageRank计算得到。Google不断的重复计算每个页面的PageRank。如果给每个页面一个随机PageRank值（非0），那么经过不断的重复计算，这些页面的PR值会趋向于稳定，也就是收敛的状态。这就是搜索引擎使用它的原因。

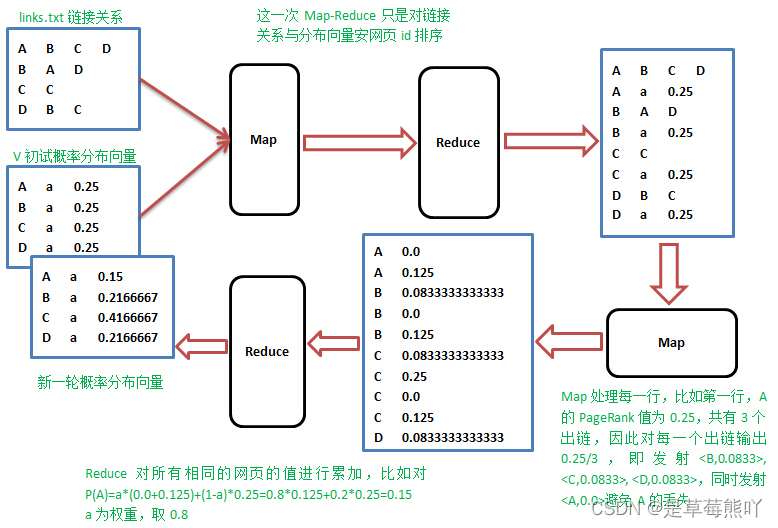
三、一个PageRank模型的简单完整实例

互联网中的网页可以看出是一个有向图，其中网页是结点，如果网页A有链接到网页B，则存在一条有向边A->B，如：

如果一个网页有k条出链，那么跳转到任意一个出链上的概率是1/k，一般用转移矩阵来表示页面间的跳转概率，如果用n表示网页的数目，则转移矩阵M是一个n*n的方阵；如果页面j有k个出链，那么对每一个出链指向的页面i，有M[i][j]=1/k，而其他网页的M[i][j]=0；上面示例图对应的转移矩阵如下：

初始时，假设上网者在每个页面的概率都是相等的，即1/n，于是初始的概率分布就是一个所有值都为1/n的n维列向量，用去右乘转移矩阵，就得到了第一步之后上网者的概率分布向量,依旧得到一个的矩阵。下面是的计算过程：

注意，矩阵中不为零表示用一个链接从j指向i，的第一行乘以，表示累加所有网页到网页A的概率即得到11/24。得到后，再用去右乘得到，一直乘下去，最终会收敛，即，根据上面的图例，循环迭代，最终：

四、终止点问题

上述行为是一个马尔科夫过程的实例，要满足收敛性，需要具备一个条件：图是强连通的，即从任意网页可以到达其他任意网页。

但是，互联网上的网页不满足强连通的特性，因为有些网页不指向任何网页，如果按照上面的计算，上网者到达这样的网页后便走投无路，导致前面累积得到的转移概率被清零，这样下去，最终得到的概率分布向量所有元素几乎都为零。假如我们把上面图中C到A的链接丢掉，C变成了一个终止点，得到下面这个图：

对应的转移矩阵为：

循环迭代下去，最终所有元素都为零：

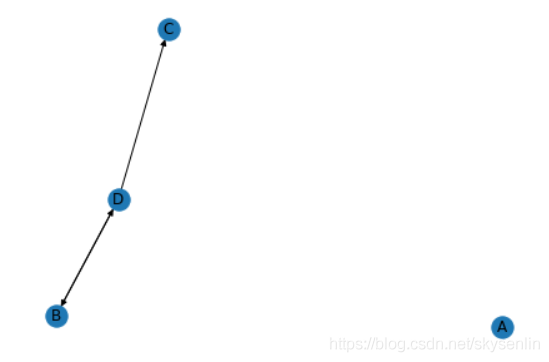
五、陷阱问题

另外一个问题就是陷阱问题，即有些网页不存在指向其他网页的链接，但存在指向自己的链接。比如下面这个图：

上网者到C网页之后，就像跳进了陷阱，陷入了漩涡，再也不能从C中出来，将最终导致概率分布值全部转移到C上来，这使得其他网页的概率分布值为零，从而整个网页排名就失去了意义。如果按照上面的图对应的转移矩阵为：

循环迭代下去，就变成了这样：

六、解决终止点问题和陷阱问题

上面的过程，我们忽略了一个问题，那就是每个网页上面都有一个地址栏，当上网者走到一个陷阱网页（比如上面两例中的网页C），他可以在浏览器的地址栏随机输入一个地址跳出去（这是对该算法的改进），而每一步，上网者都有可能不想看当前网页了，不看当前网页也就不会点击上面的链接，而是在地址栏输入另外一个网址，而在地址栏输入各个网址跳转的概率是相等的，各为1/n。假设，上网者每一步查看当前网页的概率为，那么他从浏览器地址栏跳转的概率为，于是原来的迭代公式转化为：

现在我们来计算带陷阱的网页图的概率分布（这里我们设为0.8）：

循环迭代，得到：

七、PageRank代码实现

spark实现简单的pagerank

本文链接：https://blog.csdn.net/u010506130/article/details/52222849

import org.apache.spark.api.java.JavaPairRDD;
import org.apache.spark.api.java.JavaSparkContext;
import org.apache.spark.api.java.JavaRDD;
import org.apache.spark.SparkConf;
import org.apache.spark.api.java.function.Function;
import org.apache.spark.api.java.function.Function2;
import org.apache.spark.api.java.function.PairFunction;
import org.apache.spark.api.java.function.PairFlatMapFunction;
import scala.Tuple2;import java.util.*;public class PageRank{public static void main(String[] args){SparkConf conf=new SparkConf();conf.setAppName("pagerank");conf.setMaster("local");conf.set("spark.testing.memory", "500000000");//设置运行内存大小JavaSparkContext sc=new JavaSparkContext(conf);//partitionBy()只对kv RDD起作用, 进行该操作后，将相同key值的数据放到同一机器上，并进行持久化操作，对后续循环中的join操作进行优化，使得省去join操作 shuffle的开销ArrayList<String> list=new ArrayList<String>(4);list.add("A,D");//网页之间的连接关系，A页面链接到网页Dlist.add("B,A");list.add("C,A,B");list.add("D,A,C");JavaRDD<String> links=sc.parallelize(list);JavaPairRDD<Character,char[]> pairs =links.mapToPair(new PairFunction<String, Character, char[]>() {public Tuple2<Character,char[]> call(String s) {String[] str=s.split(",");char[] ch=new char[str.length];for (int i=0;i<str.length;i++){ch[i]=str[i].charAt(0);}return new Tuple2<Character,char[]>(s.charAt(0),ch );}//将字符串中保存的页面的链接关系map转换成key-values形式，key当前页面，指向的页面集合用数组表示}).cache();//持久化JavaPairRDD<Character,Float> ranks=sc.parallelize(Arrays.asList('A','B','C','D')).mapToPair(new PairFunction<Character, Character, Float>() {public Tuple2<Character,Float> call(Character character) throws Exception {return new Tuple2<Character,Float>(character,new Float(1.0));}//初始化页面权值是1.0});for(int i=0;i<10;i++){JavaPairRDD<Character,Tuple2<char[],Float>> contribs=pairs.join(ranks);JavaPairRDD<Character,Float> con=contribs.flatMapToPair(new PairFlatMapFunction<Tuple2<Character,Tuple2<char[],Float>>,Character,Float>(){public Iterator call(Tuple2<Character,Tuple2<char[],Float>> val) throws Exception{List<Tuple2<Character,Float>> list=new ArrayList<Tuple2<Character, Float>>();Float f=val._2._2;char[] ch=val._2._1();int len=ch.length;for(int i=0;i<len;i++) {Tuple2<Character, Float> map = new Tuple2<Character, Float>(new Character(ch[i]), new Float(f / len));list.add(map);}return list.iterator();}});//将每个页面获得其他页面的pagerank值形成键值对的形式ranks=con.reduceByKey(new Function2<Float, Float, Float>() {public Float call(Float a, Float b) { return a + b; }}).mapValues(new Function<Float, Float>() {public Float call(Float a) throws Exception {return new Float(0.15+0.85*a);}});//当前迭代的pagerank计算}Map map=ranks.collectAsMap();//访问所有页面的pagerank值Set set=map.keySet();Iterator it=set.iterator();while(it.hasNext()){System.out.println(map.get(it.next())  );}//rank.saveAsTextFile("hdfs://172.20.35.85:9000/output/pagerank/scala");}
}

PageRank的scala版本

import org.apache.log4j.{Level, Logger}
import org.apache.spark.{HashPartitioner, SparkConf, SparkContext}/*** Created by YanqingAn on 2017/1/13.*/
object PageRank {def main(args: Array[String]): Unit = {Logger.getLogger("org").setLevel(Level.ERROR)val conf = new SparkConf().setAppName("PageRank").setMaster("local")val sc = new SparkContext(conf)/*** 这里的K:V为：当前页面:当前页面的出链集合；* 而相对于出链集合当中的每一个元素，当前页面则是其入链。** 设置哈希分区为10；** 这里假设links RDD是一个很大的静态数据集，* 并且在每次迭代中都会和ranks发生连接操作，会通过网络进行数据混洗，开销很大，* 所以我们通过预先进行分区来减小网络开销；** 出于同样的原因，我们调用links的persist()方法，将它保留在内存中以供每次迭代时用。*/val links = sc.parallelize(List(("A",List("B","C")),("B",List("A","D")),("C",List("A")),("D",List("A","B","C")))).partitionBy(new HashPartitioner(10)).persist()/*** 将每个页面的排序值初始化为(1.0/4);* 由于使用mapValues,生成的RDD的分区方式会和其父RDD(links)的分区方式一样。*/var ranks = links.mapValues(v => 0.25)/*** 一般来讲，只要10次左右的迭代基本上就收敛了;* 此循环迭代的涵义是：* 1、links.join(ranks):连接两个RDD，结果类型为：Array[(String, (List[String], Double))]，*   即：Array((A,(List(B, C, D),0.25)), (B,(List(A, D),0.25)), (C,(List(A),0.25)), (D,(List(B, C),0.25)))。* 2、case(...)中links.map(dest => (dest, rank / links.size)):*   算出当前页面(pageId)对其出链集合(links)中的每一个出链(link)排序的贡献(rank / links.size)；*   此时，contributions的值为：当前页面每一个出链的页面ID和其排序值(RDD[(String, Double)])* 3、然后再把contributions按照页面ID(根据获得共享的页面)分别累加起来，*   把该页面的排序值(ranks)设为 0.2*0.25 + 0.8*contributionReceived，*   其中，0.8为查看当前页面的概率，0.2为直接从浏览器地址栏跳转的概率。*/for(i <- 0 until 10){val contributions = links.join(ranks).flatMap{case(pageId, (links, rank)) =>links.map(link => (link, rank / links.size))}ranks = contributions.reduceByKey((x,y) => x+y).mapValues(v => 0.2*0.25 + 0.8*v)}ranks.collect().foreach(println)}
}