3.5 运用派生输入方向的方法

这是一篇有关《统计学习基础》，原书名The Elements of Statistical Learning的学习笔记，该书学习难度较高，有很棒的学者将其翻译成中文并放在自己的个人网站上，翻译质量非常高，本博客中有关翻译的内容都是出自该学者的网页，个人解读部分才是自己经过查阅资料和其他学者的学习笔记，结合个人理解总结成的原创内容。
有关ESL更多的学习笔记的markdown文件，可在作者GitHub上查看下载。

原文	The Elements of Statistical Learning
翻译	szcf-weiya
时间	2018-08-21
解读	Hytn Chen
更新	2020-02-20

翻译原文

!!! note “weiya 注：翻译”
Derived Input Directions 翻译为“派生输入方向”．

在很多情形下我们有很多输入，这些输入的相关性经常是非常强的．这一小节中的方法产生较少的原输入变量 $X_j$ 的线性组合 $Z_m,m=1,2,\dots ,M$，然后 $Z_m$ 用来代替 $X_j$ 来作为回归的输入．这些方法区别于怎样构造线性组合．

主成分回归

在这种方法下，使用的线性组合 $Z_m$ 是在前面 3.4.1 节中定义的主成分．

主成分回归构造派生的输入列 ${\mathbf{z}}_m=\mathbf{X}{v}_m$，然后在 ${\mathbf{z}}_1,{\mathbf{z}}_2,\dots ,{\mathbf{z}}_M,M\le p$ 上回归 $\mathbf{y}$．因为 ${\mathbf{z}}_m$ 是正交的，则这个回归只是单变量回归的和

$${\hat{\mathbf{y}}}_{(M)}^{pcr}=\bar{y}1+\sum _{m=1}^M{\hat{\theta }}_m{\mathbf{z}}_m\text{\hspace{1em}(3.61)}$$

其中，${\hat{\theta }}_m=⟨{\mathbf{z}}_m,\mathbf{y}⟩/⟨{\mathbf{z}}_m,{\mathbf{z}}_m⟩$．（该表示法详见ESL3.2）因为每个 ${\mathbf{z}}_m$ 是原输入变量 ${\mathbf{x}}_j$ 的线性组合，我们可以将解 (3.61) 表达成关于 ${\mathbf{x}}_j$ 的系数（练习 3.13）:

$${\hat{\beta }}^{pcr}(M)=\sum _{m=1}^M{\hat{\theta }}_m{v}_m\text{\hspace{1em}(3.62)}$$

岭回归下，主成分依赖输入 ${\mathbf{x}}_j$ 的放缩尺度，所以一般地我们首先对它们进行标准化．注意到如果 $M=p$，我们就会回到通常的最小二乘估计，因为列 $\mathbf{Z}=\mathbf{U}\mathbf{D}$ 张成了 $\mathbf{X}$ 的列空间．对于 $M<p$ 我们得到一个降维的回归问题．我们看到主成分回归与岭回归非常相似：都是通过输入矩阵的主成分来操作的．岭回归对主成分系数进行了收缩，收缩更多地依赖对应特征值的大小；主成分回归丢掉 $p-M$ 个最小的特征值分量．图 3.17 说明了这一点

图 3.17 岭回归运用 (3.47) 中的收缩因子 $d_j^2/(d_j^2+\lambda )$ 来收缩主成分回归的系数．主成分回归截断了它们． 图中显示了图 3.7 对应的收缩和截断模式作为主成分指标的函数．

在图 3.7 中我们看到交叉验证表明有 7 项；最终模型在表 3.3 中有最低的测试误差．

偏最小二乘

这个技巧也构造了一系列用于回归的输入变量的线性组合，但是与主成分回归不同的是它采用 $\mathbf{y}$（除了 $\mathbf{X}$）来构造．和主成分回归相同的是，偏最小二乘 (PLS) 也不是尺度不变 (scale invariant) 的，所以我们假设每个 ${\mathbf{x}}_j$ 标准化使得均值为 0 、方差为 1．一开始，PLS 对每个 $j$ 计算 ${\hat{\phi }}_{1j}=⟨{\mathbf{x}}_j,\mathbf{y}⟩$．从这里我们构造新的派生输入变量 ${\mathbf{z}}_1={\sum }_j{\hat{\phi }}_{1j}{\mathbf{x}}_j$，这是第一偏最小二乘方向．因此在每个 ${\mathbf{z}}_m$ 的构造中，输入变量通过判断其在 $\mathbf{y}$ 上的单变量影响强度来加权．

!!! note “weiya 注：原书脚注”
因为 ${\mathrm{x}}_{\mathrm{j}}$ 已经标准化，第一方向 ${\hat{\phi }}_{1j}$ 是单变量回归的系数（乘以某不相关的常数）；但对接下来的方向不是这样．

输出变量 $\mathbf{y}$ 在 ${\mathbf{z}}_1$ 上回归便得到系数 ${\hat{\theta }}_1$，然后我们对 ${\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_p$ 进行关于 ${\mathbf{z}}_1$ 的正交化．我们继续这个过程，直到得到 $M\le p$ 个方向．在这种方式下，偏最小二乘得到一系列派生的、正交化的输入或者方向 ${\mathbf{z}}_1,{\mathbf{z}}_2,\dots ,{\mathbf{z}}_M$．和主成分回归一样，如果我们构造所有 $M=p$ 个方向，我们会得到一个等价于普通最小二乘估计的解；如果使用 $M<p$ 个方向会得到一个低维的回归．这个过程将在算法 3.3 中详细描述．

!!! note “weiya 注：”
在 $\mathbf{a}$ 上回归 $\mathbf{b}$（或者称作 $\mathbf{b}$ 在 $\mathbf{a}$ 上回归）指的是
$\mathbf{b}$ 在 $\mathbf{a}$ 上的无截距的简单单变量回归，回归系数为
$$\hat{\gamma }=\frac{⟨\mathbf{a},\mathbf{b}⟩}{⟨\mathbf{a},\mathbf{a}⟩}$$
​ 同时这一过程也称作 $\mathbf{b}$ 关于 $\mathbf{a}$ 正交化

---

算法 3.3 偏最小二乘

---

1. 对${\mathbf{x}}_j$标准化使得均值为0、方差为1.令${\hat{\mathbf{y}}}^{(0)}=\bar{y}1$, 并且${\mathbf{x}}_j^{(0)}={\mathbf{x}}_j,j=1,\dots ,p$.
2. 对于$m=1,2,\dots ,p$
   1. ${\mathbf{z}}_m={\sum }_{j=1}^p{\hat{\phi }}_{mj}{\mathbf{x}}_j^{(m-1)}$, 其中${\hat{\phi }}_{mj}=⟨{\mathbf{x}}_j^{(m-1)},\mathbf{y}⟩$
   2. ${\hat{\theta }}_m=⟨{\mathbf{z}}_m,\mathbf{y}⟩/⟨{\mathbf{z}}_m,{\mathbf{z}}_m⟩$
   3. ${\hat{\mathbf{y}}}^{(m)}={\hat{\mathbf{y}}}^{(m-1)}+{\hat{\theta }}_m{\mathbf{z}}_m$
   4. 对每个${\mathbf{x}}_j^{(m-1)}$关于${\mathbf{z}}_m$正交化：${\mathbf{x}}_j^{(m)}={\mathbf{x}}_j^{(m-1)}-\frac{⟨{\mathbf{z}}_m,{\mathbf{x}}_j⟩}{⟨{\mathbf{z}}_m,{\mathbf{z}}_m⟩}{\mathbf{z}}_m,j=1,2,\dots ,p.$
3. 输出拟合向量序列 { y ( m ) ^ } 1 p \{\hat{\mathbf y^{(m)}}\}^p_1 {y(m)^​}1p​．因为 { z ℓ } 1 m \{\mathbf z_\ell\}^m_1 {zℓ​}1m​关于原输入变量${\mathbf{x}}_j$为线性的，所以是${\hat{\mathbf{y}}}^{(m)}=\mathbf{X}{\hat{\beta }}^{pls}(m)$.这些线性系数可以通过PLS转换的序列重新得到．

在前列腺癌的例子中，交叉验证在图 3.7 中选择 $M=2$ 个 PLS 方向．这得到了表 3.3 最右边的列的模型．

偏最小二乘求解的是什么优化问题呢？因为它使用响应变量 $\mathbf{y}$ 去构造它的方向，所以它解的路径是关于 $\mathbf{y}$ 的非线性函数．可以证明（练习 3.15）偏最小二乘寻找有高方差以及和响应变量有高相关性的方向，而与之相对的主成分分析回归只重视高方差（Stone and Brooks, 1990¹; Frank and Friedman, 1993²）．特别地，第 $m$ 个主成分方向 $v_m$ 是下面问题的解：

$$\begin{array}{rl}\underset{\alpha }{\max }& \mathrm{V}\mathrm{a}\mathrm{r}(\mathbf{X}\alpha )\\ \mathrm{s}\mathrm{t}& \Vert \alpha \Vert =1,{\alpha }^T\mathbf{S}{v}_{\ell }=0,\ell =1,\dots ,m-1\end{array}\text{\hspace{1em}(3.63)}$$

其中，$\mathbf{S}$ 为 ${\mathbf{x}}_j$ 的样本协方差矩阵．${\alpha }^T\mathbf{S}{v}_{\ell }=0$ 保证了 ${\mathbf{z}}_m=\mathbf{X}\alpha$ 与之前所有的线性组合 ${\mathbf{z}}_{\ell }={\mathbf{v}}_{\ell }$ 都不相关．第 $m$ 个 PLS 方向 ${\hat{\phi }}_m$ 是下面的解：

$$\begin{array}{rl}\underset{\alpha }{\max }& {\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}}^2(\mathbf{y},\mathbf{X}\alpha )\mathrm{V}\mathrm{a}\mathrm{r}(\mathbf{X}\alpha )\\ \mathrm{s}\mathrm{t}& \Vert \alpha \Vert =1,{\alpha }^T\mathbf{S}{\hat{\phi }}_{\ell }=0,\ell =1,\dots ,m-1\end{array}\text{\hspace{1em}(3.64)}$$

进一步的分析揭示了，方差项趋向于占主导地位，而且因此偏最小二乘表现得很像岭回归和主成分回归．我们将在下一节讨论这些．

如果输入矩阵 $\mathbf{X}$ 是正交的，则偏最小二乘会经过 $m=1$ 步找到最小二乘估计．后续的步骤不起作用，因为 $m>1\text{时}，{\hat{\phi }}_{mj}=0$（练习 3.14）．

也可以证明 $m=1,2,\dots ,p$ 时的 PLS 系数序列表示计算最小二乘解时的共轭梯度（练习 3.18）．

regression tools (with discussion), Technometrics 35(2): 109–148.

个人解读

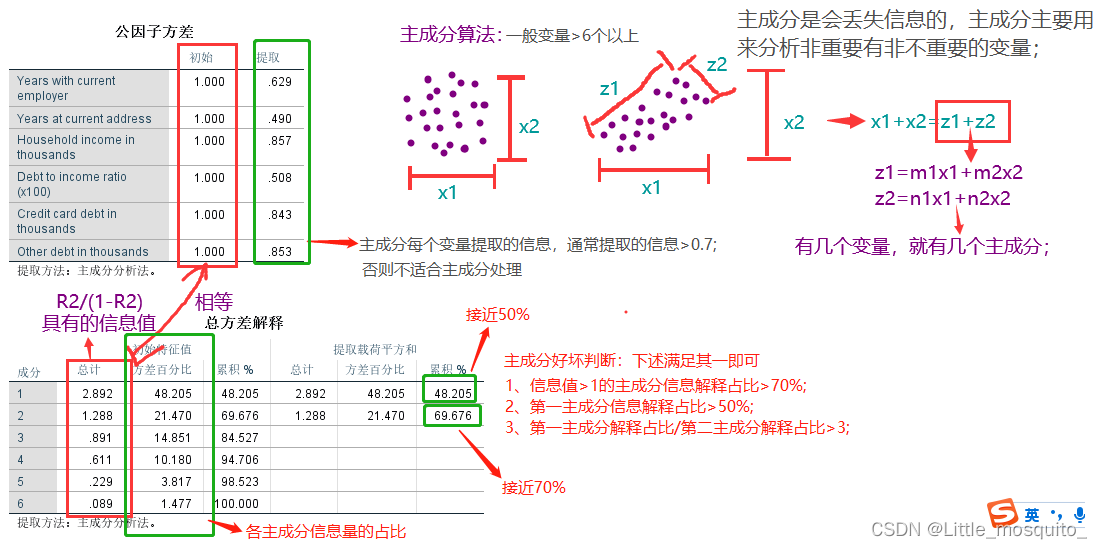
主成分分析基本思想

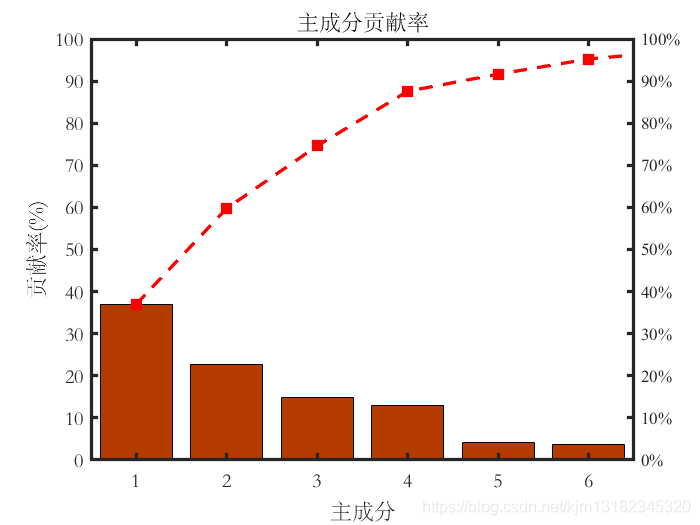
这段概念基于特征值与特征向量展开，主成分分析是利用降维的思想，将多个变量转化为少数几个综合变量（即主成分），其中每个主成分都是原始变量的线性组合，各主成分之间互不相关，从而这些主成分能够反映始变量的绝大部分信息，且所含的信息互不重叠。它是一个线性变换，这个变换把数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上，第二大方差在第二个坐标(第二主成分)上，依次类推。主成分分析经常用减少数据集的维数，同时保持数据集的对方差贡献最大的特征。

对特征值与特征向量博客的两个解读（该文解释的特征值与特征向量有助于理解主成分分析，值得详读）

对于BU的理解：实现了数据集在特征向量这组正交基上的投影，其实，这里的正交基就是用一组新的U来代替了原本的X，就像书中之前的公式讲的那样，是线性变换。注意U是对称阵，所以计算才make sense，才是投影。

对特征值的理解：参考这篇博客。其实就是这个待分解的矩阵B，其作用于特征向量上不会改变特征向量的方向，所以特征向量和矩阵的本质有关，但是如果矩阵把特征向量进行线性变换后拉伸的值越大，那这个特征向量就越具备代表意义。

对于偏最小二乘的算法部分描述如下

算法 3.3 偏最小二乘

---

1. 对${\mathbf{x}}_j$标准化使得均值为0、方差为1.令${\hat{\mathbf{y}}}^{(0)}=\bar{y}1$, 并且${\mathbf{x}}_j^{(0)}={\mathbf{x}}_j,j=1,\dots ,p$.
2. 对于$m=1,2,\dots ,p$
   1. ${\mathbf{z}}_m={\sum }_{j=1}^p{\hat{\phi }}_{mj}{\mathbf{x}}_j^{(m-1)}$, 其中${\hat{\phi }}_{mj}=⟨{\mathbf{x}}_j^{(m-1)},\mathbf{y}⟩$
   2. ${\hat{\theta }}_m=⟨{\mathbf{z}}_m,\mathbf{y}⟩/⟨{\mathbf{z}}_m,{\mathbf{z}}_m⟩$
   3. ${\hat{\mathbf{y}}}^{(m)}={\hat{\mathbf{y}}}^{(m-1)}+{\hat{\theta }}_m{\mathbf{z}}_m$
   4. 对每个${\mathbf{x}}_j^{(m-1)}$关于${\mathbf{z}}_m$正交化：${\mathbf{x}}_j^{(m)}={\mathbf{x}}_j^{(m-1)}-\frac{⟨{\mathbf{z}}_m,{\mathbf{x}}_j⟩}{⟨{\mathbf{z}}_m,{\mathbf{z}}_m⟩}{\mathbf{z}}_m,j=1,2,\dots ,p.$
3. 输出拟合向量序列 { y ( m ) ^ } 1 p \{\hat{\mathbf y^{(m)}}\}^p_1 {y(m)^​}1p​．因为 { z ℓ } 1 m \{\mathbf z_\ell\}^m_1 {zℓ​}1m​关于原输入变量${\mathbf{x}}_j$为线性的，所以是${\hat{\mathbf{y}}}^{(m)}=\mathbf{X}{\hat{\beta }}^{pls}(m)$.这些线性系数可以通过PLS转换的序列重新得到．

对于第二步的第一部分，其实这里的${\mathbf{x}}_j$和$\mathbf{y}$之所以是向量是因为有N个样本，而系数就可以理解为两个向量的点乘，点乘感性理解可以代表相似度。那如何计算当前m步下的${\mathbf{z}}_m$呢？当m是1的时候，所有的x都是标准化的，所以把每个单变量在y上面的影响强度作为权重，先加权求和得出第一个方向${\mathbf{z}}_1$。

对于第二步的第二部分，就是将y在该方向上进行回归，得到系数${\hat{\theta }}_m$。

对于第二步的第三部分，就是把当前方向上的分量加进之前的预测向量中去，进一步接近$\hat{\mathbf{y}}$。

对于第二步的第四部分相当于对于每个${\mathbf{x}}_j$，减去其在${\mathbf{z}}_m$投影的部分（在${\mathbf{z}}_m$上回归${\mathbf{x}}_j$得到系数再乘${\mathbf{z}}_m$），留下的残差向量就是和${\mathbf{z}}_m$正交的部分，该步骤相关概念的理解可参考ESL3.2的图3.4。感性理解就是，${\mathbf{z}}_m$这个方向已经计算结束分离出来了，需要将其在其他x上面的分量全都清离出去，也就是对每个${\mathbf{x}}_j^{(m-1)}$关于${\mathbf{z}}_m$正交化。

---

1. Stone, M. and Brooks, R. J. (1990). Continuum regression: cross-validated sequentially constructed prediction embracing ordinary least squares, partial least squares and principal components regression (Corr: V54 p906-907), Journal of the Royal Statistical Society, Series B 52: 237–269. ↩︎

2. Frank, I. and Friedman, J. (1993). A statistical view of some chemometrics ↩︎