概述和定义
在本文中,我们将考虑一些线性模型的替代拟合方法,除了通常的 普通最小二乘法。这些替代方法有时可以提供更好的预测准确性和模型可解释性。最近我们被客户要求撰写关于模型选择的研究报告,包括一些图形和统计输出。
主成分分析PCA降维方法和R语言分析葡萄酒可视化实例
主成分分析PCA降维方法和R语言分析葡萄酒可视化实例
,时长04:30
- 预测精度:线性,普通最小二乘估计将具有低偏差。OLS也表现良好, n >> p。但是,如果 n 不比p大很多 ,则拟合可能会有很多可变性,从而导致拟合过度和/或预测不佳。如果 p > n,则不再有唯一的最小二乘估计,并且根本无法使用该方法。
这个问题是维数诅咒的另一个方面 。当 p 开始变大时,观测值 x 开始变得比附近的观测值更接近类别之间的边界,这给预测带来了主要问题。此外,对于许多 p,训练样本经常是稀疏的,从而难以识别趋势和进行预测。
通过 限制 和 缩小 估计的系数,我们通常可以大大减少方差,因为偏差的增加可忽略不计,这通常会导致准确性的显着提高。
-
模型的可解释性:不相关的变量导致结果模型不必要的复杂性。通过删除它们(设置系数= 0),我们得到了一个更容易解释的模型。但是,使用OLS使得系数极不可能为零。
-
子集选择:我们使用子集特征的最小二乘拟合模型。
-
尽管我们讨论了这些技术在线性模型中的应用,但它们也适用于其他方法,例如分类。
详细方法
子集选择
最佳子集选择
在这里,我们为p个 预测变量的每种可能组合拟合单独的OLS回归 ,然后查看结果模型拟合。这种方法的问题在于, 最佳模型 隐藏在2 ^ p种 可能性之内。该算法分为两个阶段。(1)拟合所有包含k个预测变量的模型 ,其中 k 是模型的最大长度。(2)使用交叉验证的预测误差选择一个模型。下面将讨论更具体的预测误差方法,例如AIC和BIC。
这适用于其他类型的模型选择,例如逻辑回归,但我们根据选择选择的得分会有所变化。对于逻辑回归,我们将使用 偏差 而不是RSS和R ^ 2。
选择最佳模型
上面提到的三种算法中的每一种都需要我们手动确定哪种模型效果最好。如前所述,使用训练误差时,具有最多预测值的模型通常具有最小的RSS和最大的R ^ 2。为了选择测试 误差最大的模型 ,我们需要估计测试误差。有两种计算测试误差的方法。
-
通过对训练误差进行和调整来间接估计测试误差,以解决过度拟合的偏差。
-
使用验证集或交叉验证方法直接估计测试错误。
验证和交叉验证
通常,交叉验证技术是对测试的更直接估计,并且对基础模型的假设更少。此外,它可以用于更广泛的模型类型选择中。
岭回归
岭回归与最小二乘相似,不同之处在于系数是通过最小化略有不同的数量来估算的。像OLS一样,Ridge回归寻求降低RSS的系数估计,但是当系数接近于零时,它们也会产生收缩损失。这种损失的作用是将系数估计值缩小到零。参数λ控制收缩的影响。λ= 0的行为与OLS回归完全相同。当然,选择一个好的λ值至关重要,应该使用交叉验证进行选择。岭回归的要求是预测变量 X的 中心定为 mean = 0,因此必须事先对数据进行标准化。
相关 视频:Lasso回归、岭回归等正则化回归数学原理及R语言实例
Lasso回归、岭回归等正则化回归数学原理及R语言实例
为什么岭回归比最小二乘更好?
优势在偏差方差中显而易见 。随着λ的增加,岭回归拟合的灵活性降低。这导致方差减小,偏差增加较小。固定的OLS回归具有较高的方差,但没有偏差。但是,最低的测试MSE往往发生在方差和偏差之间的交点处。因此,通过适当地调整λ获取较少的方差,我们可以找到较低的潜在MSE。
在最小二乘估计具有高方差的情况下,岭回归最有效。Ridge回归比任何子集方法都具有更高的计算效率 ,因为可以同时求解所有λ值。
套索Lasso
岭回归具有至少一个缺点。它包括 最终模型中的所有 p个预测变量。惩罚项将使其中许多接近零,但永远不会 精确 为零。对于预测准确性而言,这通常不是问题,但会使模型更难以解释结果。Lasso克服了这个缺点,并且能够将s 足够小地强制将某些系数设为零 。由于 s = 1导致常规的OLS回归,因此当 s 接近0时,系数将缩小为零。因此,套索回归也执行变量选择。
降维方法
到目前为止,我们所讨论的方法已经通过使用原始变量的子集或将其系数缩小到零来控制了方差。现在,我们探索一类模型, 这些模型可以 转换预测变量,然后使用转换后的变量拟合最小二乘模型。降维将估计 p +1个系数的问题简化为M +1个系数的简单问题 ,其中 M < p。这项任务的两种方法是 主成分回归 和 偏最小二乘。
主成分回归(PCA)
可以将PCA描述为一种从大量变量中导出低维特征集的方法。
在回归中,我们构造 M个 主成分,然后在使用最小二乘的线性回归中将这些成分用作预测变量。通常,与普通最小二乘法相比,我们有可能拟合出更好的模型,因为我们可以减少过度拟合的影响。
偏最小二乘
我们上面描述的PCR方法涉及鉴定 最能代表预测变量的X的线性组合 。
PLS通过对与因变量最密切相关的变量赋予更高的权重来实现此目的。
实际上,PLS的性能不比岭回归或PCR好。这是因为即使PLS可以减少偏差,它也有可能增加方差,因此总体收益并没有真正的区别。
解释高维结果
我们必须始终谨慎对待报告获得的模型结果的方式,尤其是在高维设置中。在这种情况下,多重共线性问题非常严重,因为模型中的任何变量都可以写为模型中所有其他变量的线性组合。
例子
子集选择方法
最佳子集选择
我们希望根据上一年的各种统计数据来预测棒球运动员Salary 的情况 。
library(ISLR)
attach(Hitters)
names(Hitters)## [1] "AtBat" "Hits" "HmRun" "Runs" "RBI"
## [6] "Walks" "Years" "CAtBat" "CHits" "CHmRun"
## [11] "CRuns" "CRBI" "CWalks" "League" "Division"
## [16] "PutOuts" "Assists" "Errors" "Salary" "NewLeague"dim(Hitters)## [1] 322 20str(Hitters)## 'data.frame': 322 obs. of 20 variables:
## $ AtBat : int 293 315 479 496 321 594 185 298 323 401 ...
## $ Hits : int 66 81 130 141 87 169 37 73 81 92 ...
## $ HmRun : int 1 7 18 20 10 4 1 0 6 17 ...
## $ Runs : int 30 24 66 65 39 74 23 24 26 49 ...
## $ RBI : int 29 38 72 78 42 51 8 24 32 66 ...
## $ Walks : int 14 39 76 37 30 35 21 7 8 65 ...
## $ Years : int 1 14 3 11 2 11 2 3 2 13 ...
## $ CAtBat : int 293 3449 1624 5628 396 4408 214 509 341 5206 ...
## $ CHits : int 66 835 457 1575 101 1133 42 108 86 1332 ...
## $ CHmRun : int 1 69 63 225 12 19 1 0 6 253 ...
## $ CRuns : int 30 321 224 828 48 501 30 41 32 784 ...
## $ CRBI : int 29 414 266 838 46 336 9 37 34 890 ...
## $ CWalks : int 14 375 263 354 33 194 24 12 8 866 ...
## $ League : Factor w/ 2 levels "A","N": 1 2 1 2 2 1 2 1 2 1 ...
## $ Division : Factor w/ 2 levels "E","W": 1 2 2 1 1 2 1 2 2 1 ...
## $ PutOuts : int 446 632 880 200 805 282 76 121 143 0 ...
## $ Assists : int 33 43 82 11 40 421 127 283 290 0 ...
## $ Errors : int 20 10 14 3 4 25 7 9 19 0 ...
## $ Salary : num NA 475 480 500 91.5 750 70 100 75 1100 ...
## $ NewLeague: Factor w/ 2 levels "A","N": 1 2 1 2 2 1 1 1 2 1 ...# 检察缺失值
sum(is.na(Hitters$Salary))/length(Hitters[,1])*100## [1] 18.32事实证明,大约有18%的数据丢失。我们将省略丢失的数据。
Hitters <- na.omit(Hitters)
dim(Hitters)## [1] 263 20执行最佳子集选择,使用RSS进行量化。
library(leaps)regfit <- regsubsets(Salary ~ ., Hitters)
summary(regfit)## Subset selection object
## Call: regsubsets.formula(Salary ~ ., Hitters)
## 19 Variables (and intercept)
## Forced in Forced out
## AtBat FALSE FALSE
## Hits FALSE FALSE
## HmRun FALSE FALSE
## Runs FALSE FALSE
## RBI FALSE FALSE
## Walks FALSE FALSE
## Years FALSE FALSE
## CAtBat FALSE FALSE
## CHits FALSE FALSE
## CHmRun FALSE FALSE
## CRuns FALSE FALSE
## CRBI FALSE FALSE
## CWalks FALSE FALSE
## LeagueN FALSE FALSE
## DivisionW FALSE FALSE
## PutOuts FALSE FALSE
## Assists FALSE FALSE
## Errors FALSE FALSE
## NewLeagueN FALSE FALSE
## 1 subsets of each size up to 8
## Selection Algorithm: exhaustive
## AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns
## 1 ( 1 ) " " " " " " " " " " " " " " " " " " " " " "
## 2 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " "
## 3 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " "
## 4 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " "
## 5 ( 1 ) "*" "*" " " " " " " " " " " " " " " " " " "
## 6 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " " "
## 7 ( 1 ) " " "*" " " " " " " "*" " " "*" "*" "*" " "
## 8 ( 1 ) "*" "*" " " " " " " "*" " " " " " " "*" "*"
## CRBI CWalks LeagueN DivisionW PutOuts Assists Errors NewLeagueN
## 1 ( 1 ) "*" " " " " " " " " " " " " " "
## 2 ( 1 ) "*" " " " " " " " " " " " " " "
## 3 ( 1 ) "*" " " " " " " "*" " " " " " "
## 4 ( 1 ) "*" " " " " "*" "*" " " " " " "
## 5 ( 1 ) "*" " " " " "*" "*" " " " " " "
## 6 ( 1 ) "*" " " " " "*" "*" " " " " " "
## 7 ( 1 ) " " " " " " "*" "*" " " " " " "
## 8 ( 1 ) " " "*" " " "*" "*" " " " " " "星号表示变量包含在相应的模型中。
## [1] 0.3215 0.4252 0.4514 0.4754 0.4908 0.5087 0.5141 0.5286 0.5346 0.5405
## [11] 0.5426 0.5436 0.5445 0.5452 0.5455 0.5458 0.5460 0.5461 0.5461在这个19变量模型中, R ^ 2单调增加。
我们可以使用内置的绘图功能来绘制RSS,adj R ^ 2, C p,AIC和BIC。
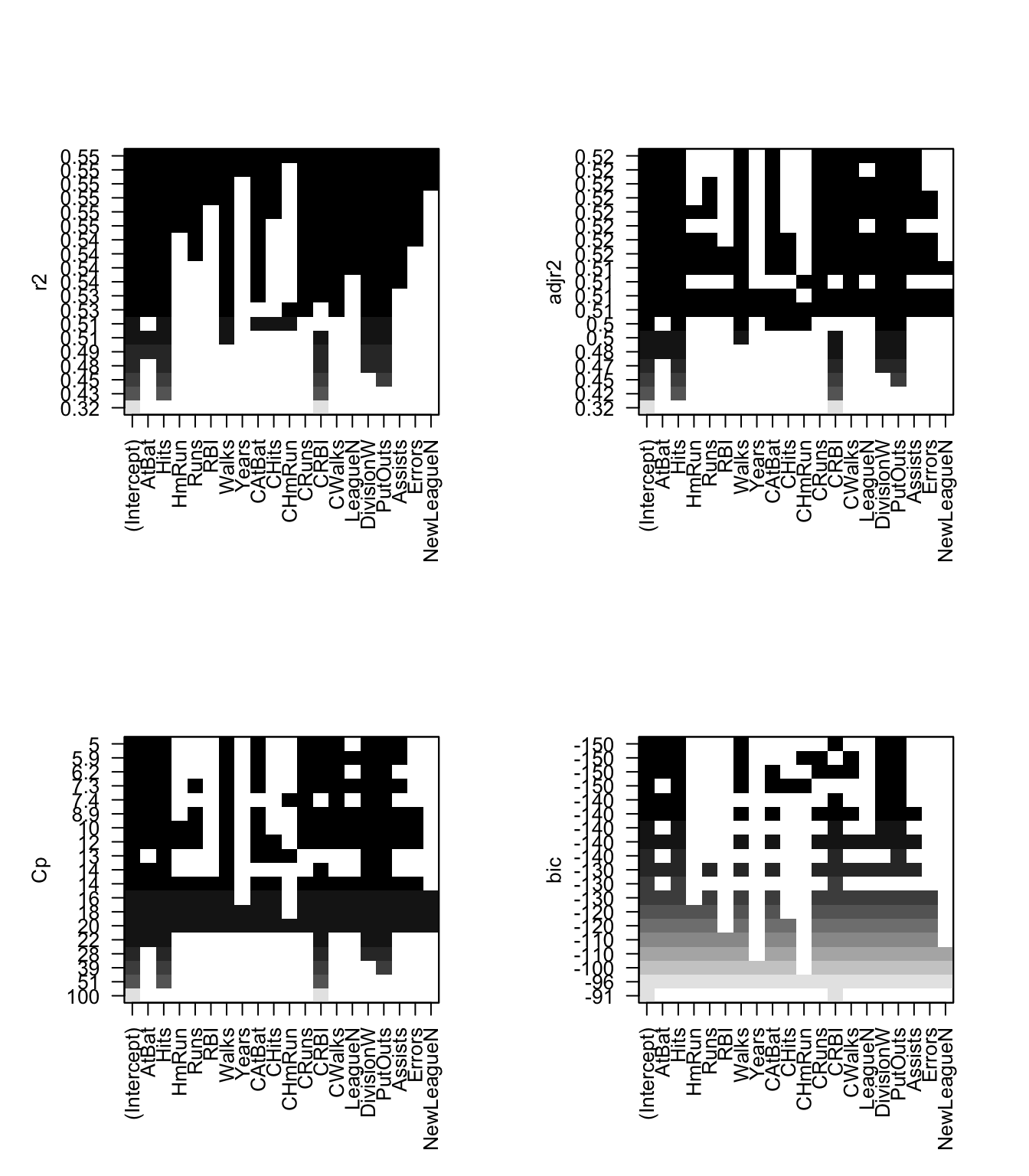
注意:上面显示的拟合度是(除R ^ 2以外)所有测试误差的估计。
向前和向后逐步选择
## Subset selection object
## Call: regsubsets.formula(Salary ~ ., data = Hitters, nvmax = 19, method = "forward")
## 19 Variables (and intercept)
## Forced in Forced out
## AtBat FALSE FALSE
## Hits FALSE FALSE
## HmRun FALSE FALSE
## Runs FALSE FALSE
## RBI FALSE FALSE
## Walks FALSE FALSE
## Years FALSE FALSE
## CAtBat FALSE FALSE
## CHits FALSE FALSE
## CHmRun FALSE FALSE
## CRuns FALSE FALSE
## CRBI FALSE FALSE
## CWalks FALSE FALSE
## LeagueN FALSE FALSE
## DivisionW FALSE FALSE
## PutOuts FALSE FALSE
## Assists FALSE FALSE
## Errors FALSE FALSE
## NewLeagueN FALSE FALSE
## 1 subsets of each size up to 19
## Selection Algorithm: forward
## AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns
## 1 ( 1 ) " " " " " " " " " " " " " " " " " " " " " "
## 2 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " "
## 3 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " "
## 4 ( 1 ) " " "*" " " " " " " " " " " " " " " " " " "
## 5 ( 1 ) "*" "*" " " " " " " " " " " " " " " " " " "
## 6 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " " "
## 7 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " " "
## 8 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " "*"
## 9 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*"
## 10 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*"
## 11 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*"
## 12 ( 1 ) "*" "*" " " "*" " " "*" " " "*" " " " " "*"
## 13 ( 1 ) "*" "*" " " "*" " " "*" " " "*" " " " " "*"
## 14 ( 1 ) "*" "*" "*" "*" " " "*" " " "*" " " " " "*"
## 15 ( 1 ) "*" "*" "*" "*" " " "*" " " "*" "*" " " "*"
## 16 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" "*" " " "*"
## 17 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" "*" " " "*"
## 18 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" " " "*"
## 19 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*"
## CRBI CWalks LeagueN DivisionW PutOuts Assists Errors NewLeagueN
## 1 ( 1 ) "*" " " " " " " " " " " " " " "
## 2 ( 1 ) "*" " " " " " " " " " " " " " "
## 3 ( 1 ) "*" " " " " " " "*" " " " " " "
## 4 ( 1 ) "*" " " " " "*" "*" " " " " " "
## 5 ( 1 ) "*" " " " " "*" "*" " " " " " "
## 6 ( 1 ) "*" " " " " "*" "*" " " " " " "
## 7 ( 1 ) "*" "*" " " "*" "*" " " " " " "
## 8 ( 1 ) "*" "*" " " "*" "*" " " " " " "
## 9 ( 1 ) "*" "*" " " "*" "*" " " " " " "
## 10 ( 1 ) "*" "*" " " "*" "*" "*" " " " "
## 11 ( 1 ) "*" "*" "*" "*" "*" "*" " " " "
## 12 ( 1 ) "*" "*" "*" "*" "*" "*" " " " "
## 13 ( 1 ) "*" "*" "*" "*" "*" "*" "*" " "
## 14 ( 1 ) "*" "*" "*" "*" "*" "*" "*" " "
## 15 ( 1 ) "*" "*" "*" "*" "*" "*" "*" " "
## 16 ( 1 ) "*" "*" "*" "*" "*" "*" "*" " "
## 17 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*"
## 18 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*"
## 19 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*"## Subset selection object
## 19 Variables (and intercept)
## Forced in Forced out
## AtBat FALSE FALSE
## Hits FALSE FALSE
## HmRun FALSE FALSE
## Runs FALSE FALSE
## RBI FALSE FALSE
## Walks FALSE FALSE
## Years FALSE FALSE
## CAtBat FALSE FALSE
## CHits FALSE FALSE
## CHmRun FALSE FALSE
## CRuns FALSE FALSE
## CRBI FALSE FALSE
## CWalks FALSE FALSE
## LeagueN FALSE FALSE
## DivisionW FALSE FALSE
## PutOuts FALSE FALSE
## Assists FALSE FALSE
## Errors FALSE FALSE
## NewLeagueN FALSE FALSE
## 1 subsets of each size up to 19
## Selection Algorithm: backward
## AtBat Hits HmRun Runs RBI Walks Years CAtBat CHits CHmRun CRuns
## 1 ( 1 ) " " " " " " " " " " " " " " " " " " " " "*"
## 2 ( 1 ) " " "*" " " " " " " " " " " " " " " " " "*"
## 3 ( 1 ) " " "*" " " " " " " " " " " " " " " " " "*"
## 4 ( 1 ) "*" "*" " " " " " " " " " " " " " " " " "*"
## 5 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " "*"
## 6 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " "*"
## 7 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " "*"
## 8 ( 1 ) "*" "*" " " " " " " "*" " " " " " " " " "*"
## 9 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*"
## 10 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*"
## 11 ( 1 ) "*" "*" " " " " " " "*" " " "*" " " " " "*"
## 12 ( 1 ) "*" "*" " " "*" " " "*" " " "*" " " " " "*"
## 13 ( 1 ) "*" "*" " " "*" " " "*" " " "*" " " " " "*"
## 14 ( 1 ) "*" "*" "*" "*" " " "*" " " "*" " " " " "*"
## 15 ( 1 ) "*" "*" "*" "*" " " "*" " " "*" "*" " " "*"
## 16 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" "*" " " "*"
## 17 ( 1 ) "*" "*" "*" "*" "*" "*" " " "*" "*" " " "*"
## 18 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" " " "*"
## 19 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" "*" "*"
## CRBI CWalks LeagueN DivisionW PutOuts Assists Errors NewLeagueN
## 1 ( 1 ) " " " " " " " " " " " " " " " "
## 2 ( 1 ) " " " " " " " " " " " " " " " "
## 3 ( 1 ) " " " " " " " " "*" " " " " " "
## 4 ( 1 ) " " " " " " " " "*" " " " " " "
## 5 ( 1 ) " " " " " " " " "*" " " " " " "
## 6 ( 1 ) " " " " " " "*" "*" " " " " " "
## 7 ( 1 ) " " "*" " " "*" "*" " " " " " "
## 8 ( 1 ) "*" "*" " " "*" "*" " " " " " "
## 9 ( 1 ) "*" "*" " " "*" "*" " " " " " "
## 10 ( 1 ) "*" "*" " " "*" "*" "*" " " " "
## 11 ( 1 ) "*" "*" "*" "*" "*" "*" " " " "
## 12 ( 1 ) "*" "*" "*" "*" "*" "*" " " " "
## 13 ( 1 ) "*" "*" "*" "*" "*" "*" "*" " "
## 14 ( 1 ) "*" "*" "*" "*" "*" "*" "*" " "
## 15 ( 1 ) "*" "*" "*" "*" "*" "*" "*" " "
## 16 ( 1 ) "*" "*" "*" "*" "*" "*" "*" " "
## 17 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*"
## 18 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*"
## 19 ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*"我们可以在这里看到1-6个变量模型对于最佳子集 和 选择是相同的 。
岭回归和套索
开始交叉验证方法
我们还将在正则化方法中应用交叉验证方法。
验证集
R ^ 2 C p和BIC估计测试错误率,我们可以使用交叉验证方法。我们必须仅使用训练观察来执行模型拟合和变量选择的所有方面。然后通过将训练模型应用于测试或验证 数据来计算测试错误 。
## Ridge Regression
##
## 133 samples
## 19 predictors
##
## Pre-processing: scaled, centered
## Resampling: Bootstrapped (25 reps)
##
## Summary of sample sizes: 133, 133, 133, 133, 133, 133, ...
##
## Resampling results across tuning parameters:
##
## lambda RMSE Rsquared RMSE SD Rsquared SD
## 0 400 0.4 40 0.09
## 1e-04 400 0.4 40 0.09
## 0.1 300 0.5 40 0.09
##
## RMSE用于使用最小值选择最佳模型。
##用于模型的最终值为lambda = 0.1。
mean(ridge.pred - test$Salary)^2## [1] 30.1k交叉验证
使用 k交叉验证选择最佳的lambda。
为了进行交叉验证,我们将数据分为测试和训练数据。
## Ridge Regression
##
## 133 samples
## 19 predictors
##
## Pre-processing: centered, scaled
## Resampling: Cross-Validated (10 fold)
##
## Summary of sample sizes: 120, 120, 119, 120, 120, 119, ...
##
## Resampling results across tuning parameters:
##
## lambda RMSE Rsquared RMSE SD Rsquared SD
## 0 300 0.6 70 0.1
## 1e-04 300 0.6 70 0.1
## 0.1 300 0.6 70 0.1
##
## RMSE用于使用最小值选择最佳模型。
##用于模型的最终值为lambda = 1e-04。# 计算相关系数
predict(ridge$finalModel, type='coef', mode='norm')$coefficients[19,]## AtBat Hits HmRun Runs RBI Walks
## -157.221 313.860 -18.996 0.000 -70.392 171.242
## Years CAtBat CHits CHmRun CRuns CRBI
## -27.543 0.000 0.000 51.811 202.537 187.933
## CWalks LeagueN DivisionW PutOuts Assists Errors
## -224.951 12.839 -38.595 -9.128 13.288 -18.620
## NewLeagueN
## 22.326sqrt(mean(ridge.pred - test$Salary)^2)## [1] 17.53因此,薪水的平均误差约为33000。回归系数似乎并没有真正趋向于零,但这是因为我们首先对数据进行了标准化。
现在,我们应该检查一下这是否比常规lm() 模型更好 。
## Linear Regression
##
## 133 samples
## 19 predictors
##
## Pre-processing: scaled, centered
## Resampling: Cross-Validated (10 fold)
##
## Summary of sample sizes: 120, 120, 121, 119, 119, 119, ...
##
## Resampling results
##
## RMSE Rsquared RMSE SD Rsquared SD
## 300 0.5 70 0.2
##
## coef(lmfit$finalModel)## (Intercept) AtBat Hits HmRun Runs RBI
## 535.958 -327.835 591.667 73.964 -169.699 -162.024
## Walks Years CAtBat CHits CHmRun CRuns
## 234.093 -60.557 125.017 -529.709 -45.888 680.654
## CRBI CWalks LeagueN DivisionW PutOuts Assists
## 393.276 -399.506 19.118 -46.679 -4.898 41.271
## Errors NewLeagueN
## -22.672 22.469sqrt(mean(lmfit.pred - test$Salary)^2)## [1] 17.62如我们所见,这种岭回归拟合当然具有较低的RMSE和较高的 R ^ 2。
套索
## The lasso
##
## 133 samples
## 19 predictors
##
## Pre-processing: scaled, centered
## Resampling: Cross-Validated (10 fold)
##
## Summary of sample sizes: 120, 121, 120, 120, 120, 119, ...
##
## Resampling results across tuning parameters:
##
## fraction RMSE Rsquared RMSE SD Rsquared SD
## 0.1 300 0.6 70 0.2
## 0.5 300 0.6 60 0.2
## 0.9 300 0.6 70 0.2
##
## RMSE用于使用最小值选择最佳模型。
##用于模型的最终值是= 0.5。## $s
## [1] 0.5
##
## $fraction
## 0
## 0.5
##
## $mode
## [1] "fraction"
##
## $coefficients
## AtBat Hits HmRun Runs RBI Walks
## -227.113 406.285 0.000 -48.612 -93.740 197.472
## Years CAtBat CHits CHmRun CRuns CRBI
## -47.952 0.000 0.000 82.291 274.745 166.617
## CWalks LeagueN DivisionW PutOuts Assists Errors
## -287.549 18.059 -41.697 -7.001 30.768 -26.407
## NewLeagueN
## 19.190sqrt(mean(lasso.pred - test$Salary)^2)## [1] 14.35在套索lasso中,我们看到许多系数已被强制为零。即使RMSE比ridge回归高一点,它也比线性回归模型具有优势。
PCR和PLS
主成分回归
## Data: X dimension: 133 19
## Y dimension: 133 1
## Fit method: svdpc
## Number of components considered: 19
##
## VALIDATION: RMSEP
## Cross-validated using 10 random segments.
## (Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps
## CV 451.5 336.9 323.9 328.5 328.4 329.9 337.1
## adjCV 451.5 336.3 323.6 327.8 327.5 328.8 335.7
## 7 comps 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps
## CV 335.2 333.7 338.5 334.3 337.8 340.4 346.7
## adjCV 332.5 331.7 336.4 332.0 335.5 337.6 343.4
## 14 comps 15 comps 16 comps 17 comps 18 comps 19 comps
## CV 345.1 345.7 329.4 337.3 343.5 338.7
## adjCV 341.2 341.6 325.7 332.7 338.4 333.9
##
## TRAINING: % variance explained
## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
## X 36.55 60.81 71.75 80.59 85.72 89.76 92.74
## Salary 45.62 50.01 51.19 51.98 53.23 53.36 55.63
## 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps 14 comps
## X 95.37 96.49 97.45 98.09 98.73 99.21 99.52
## Salary 56.48 56.73 58.57 58.92 59.34 59.44 62.01
## 15 comps 16 comps 17 comps 18 comps 19 comps
## X 99.77 99.90 99.97 99.99 100.00
## Salary 62.65 65.29 66.48 66.77 67.37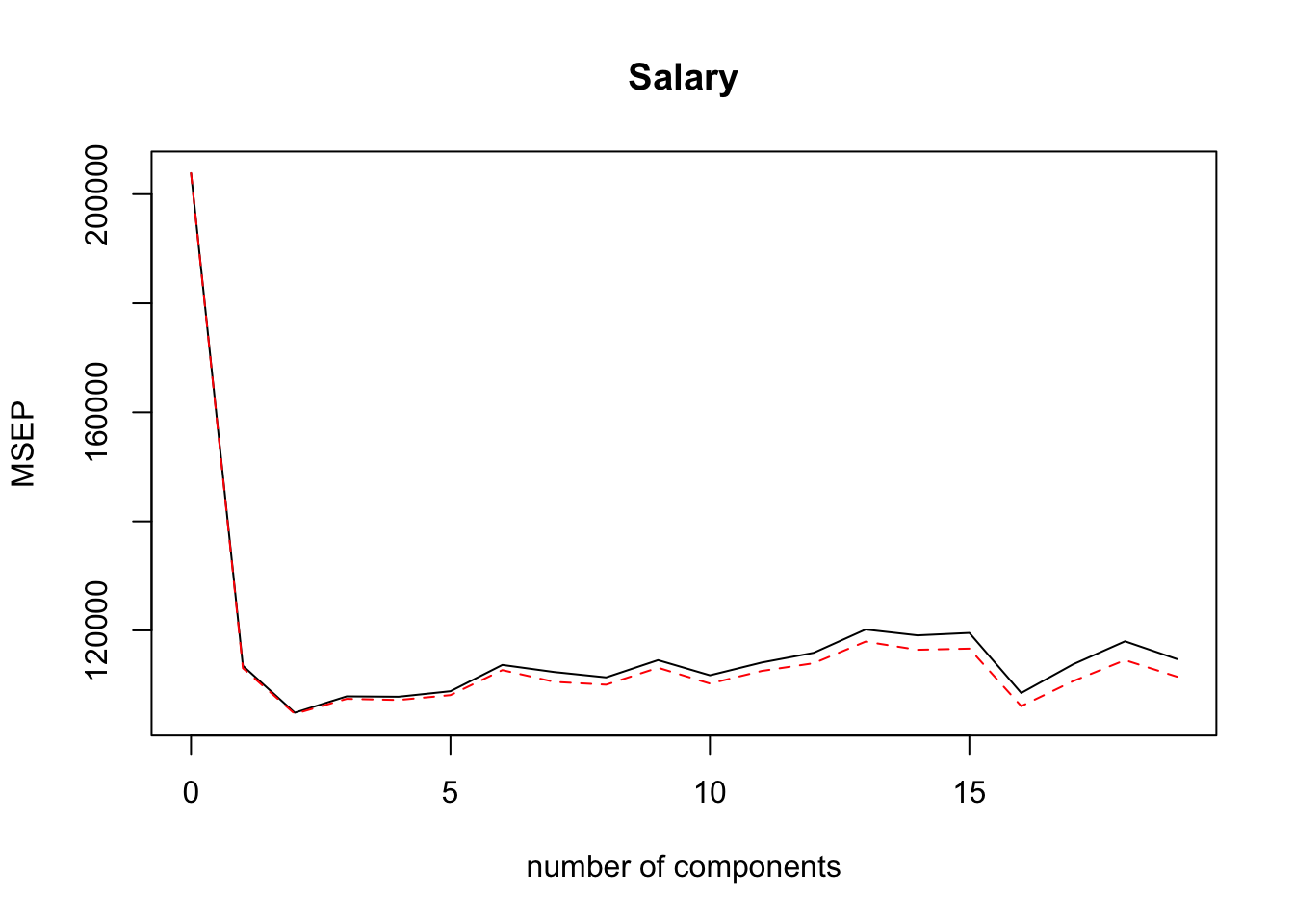
该算法将CV报告为RMSE,并将训练数据报告为R ^ 2。通过将MSE作图可以看出,我们实现了最低的MSE。这表明与最小二乘法相比有了很大的改进,因为我们能够仅使用3个分量而不是19个分量来解释大部分方差。
测试数据集上执行。
sqrt(mean((pcr.pred - test$Salary)^2))## [1] 374.8比套索/线性回归的RMSE低。
## Principal Component Analysis
##
## 133 samples
## 19 predictors
##
## Pre-processing: centered, scaled
## Resampling: Cross-Validated (10 fold)
##
## Summary of sample sizes: 121, 120, 118, 119, 120, 120, ...
##
## Resampling results across tuning parameters:
##
## ncomp RMSE Rsquared RMSE SD Rsquared SD
## 1 300 0.5 100 0.2
## 2 300 0.5 100 0.2
## 3 300 0.6 100 0.2
##
## RMSE用于使用最小值选择最佳模型。
##用于模型的最终值为ncomp = 3。选择2个成分的最佳模型
sqrt(mean(pcr.pred - test$Salary)^2)## [1] 21.86但是,PCR结果不容易解释。
偏最小二乘
## Data: X dimension: 133 19
## Y dimension: 133 1
## Fit method: kernelpls
## Number of components considered: 19
##
## VALIDATION: RMSEP
## Cross-validated using 10 random segments.
## (Intercept) 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps
## CV 451.5 328.9 328.4 332.6 329.2 325.4 323.4
## adjCV 451.5 328.2 327.4 330.6 326.9 323.0 320.9
## 7 comps 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps
## CV 318.7 318.7 316.3 317.6 316.5 317.0 319.2
## adjCV 316.2 315.5 313.5 314.9 313.6 313.9 315.9
## 14 comps 15 comps 16 comps 17 comps 18 comps 19 comps
## CV 323.0 323.8 325.4 324.5 323.6 321.4
## adjCV 319.3 320.1 321.4 320.5 319.9 317.8
##
## TRAINING: % variance explained
## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
## X 35.94 55.11 67.37 74.29 79.65 85.17 89.17
## Salary 51.56 54.90 57.72 59.78 61.50 62.94 63.96
## 8 comps 9 comps 10 comps 11 comps 12 comps 13 comps 14 comps
## X 90.55 93.49 95.82 97.05 97.67 98.45 98.67
## Salary 65.34 65.75 66.03 66.44 66.69 66.77 66.94
## 15 comps 16 comps 17 comps 18 comps 19 comps
## X 99.02 99.26 99.42 99.98 100.00
## Salary 67.02 67.11 67.24 67.26 67.37
最好的 M 为2。评估相应的测试误差 。
sqrt(mean(pls.pred - test$Salary)^2)## [1] 14.34与PCR相比,在这里我们可以看到RMSE有所改善。