主成分分析python实现
这是我一直都想写的内容,但是迟迟没有动手开始写,主要的原因是没有理解python中PCA降维后再进行回归时应该要怎么做。再网上查了很多资料,也没有这方面的讲解,书上也是讲到了PCA降维就结束了。以下是我使用R语言的思想写的code,日后若找到相关的内容再进行修改。
先介绍一下sklearn中PCA模型的参数及方法:
参数:
n_components : int,float,None或string(‘mle’)
要保留的主成分数量。如果未设置n_components,则保留所有主成分, 如果n_components = 1, 表示保留一个主成分(第一主成分)
copy : bool(默认为True)
表示是否将原始数据复制。如果为False,则传递给fit的数据将被覆盖并且运行fit(X).transform(X)将不会产生预期结果,请改用fit_transform(X)。
whiten : bool,可选(默认为False)
表示是否白化,使得每个特征具有相同的方差。
当为True(默认为False)时,components_矢量乘以n_samples的平方根,然后除以奇异值,以确保具有单位分量方差的不相关输出。
白化将从变换后的信号中去除一些信息(组件的相对方差尺度),但有时可以通过使数据遵循一些硬连线假设来提高下游估计器的预测精度。
属性
components_ : array,shape(n_components,n_features)
特征空间中的主轴,表示数据中最大方差的方向。
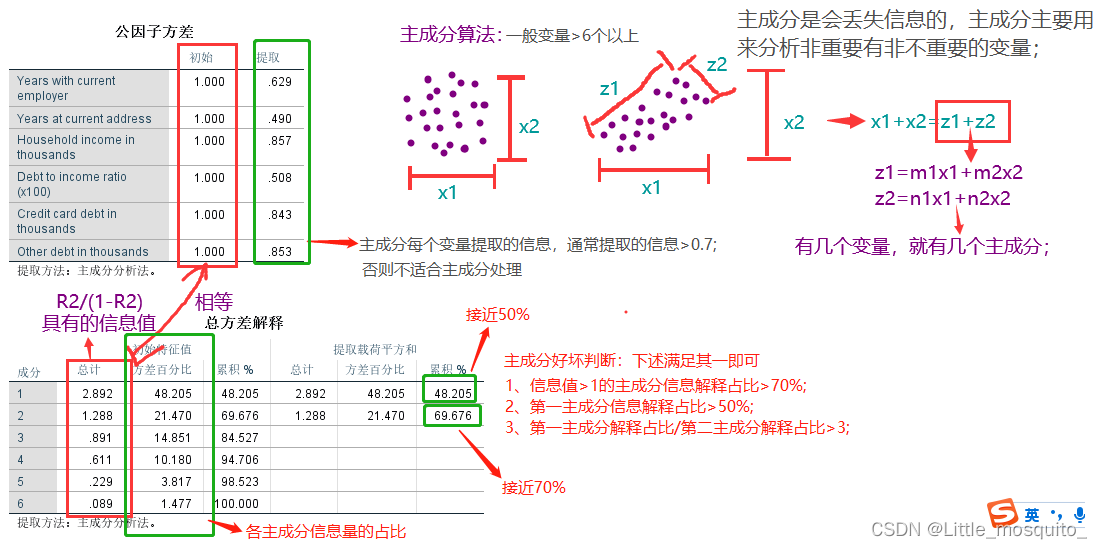
explained_variance_ : 阵列,形状(n_components,)
由每个所选主成分解释的方差量。
explained_variance_ratio_ : 阵列,形状(n_components,)
每个所选主成分解释的差异百分比。主成分方差占总方差的百分数
singular_values_ : 数组,形状(n_components,)
对应于每个所选主成分的奇异值。奇异值等于n_components 低维空间中变量的2范数。
mean_ : array,shape(n_features,)
根据训练集估计的每个特征经验均值。等于X.mean(axis=0)
n_components_ : int
主成分个数
方法:
fit(X) 用X训练模型,返回训练后的模型
fit_transform(X) 用X训练模型,返回降维后的数据 Z (主成分矩阵,可以用来建立回归模型的数据)
transform(X)
将数据X转换成降维后的数据.。 当模型训练好后,对于新输入的数据,也可以用transform方法来降维。(此时返回的数据是主成分Z, Zi = a1x1 +…+apxp)
get_covariance()
cov = components_.T * S**2 * components_ + sigma2 * eye(n_features)
其中S ** 2包含解释的方差,sigma2包含噪声方差。
计算与生成模型的数据协方差。返回估计的协方差
get_params()
获取生成该模型时所传入的参数
get_precision()
用生成的模型计算数据精度矩阵
inverse_transform(X )
返回原始数据X, 这可能跟未转换前的原始数据有所差别,但是差别不是很大
score(X)
返回所有样本的平均对数似然。
score_samples(X )
返回每个样本的对数似然
案例实现
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split# 读取数据
data = pd.read_csv(filepath , encoding = 'UTF-8')
注:原始数据中有5个变量,一个因变量.
1、 对数据进行标准化处理 (pca中默认的标准化是直接减去均值,但是在建模的过程中,感觉这样子不是很好,所以我先对数据进行标准化处理,而后才进行pca降维操作
对于标准化的方法有很多, 有兴趣的可以参考这篇文章:常用的数据标准化方法
我这里采用的是z_score标准化方法(x - u)/sigma
# 对数据进行标准化
X = (X - X.mean())/np.std(X)
Y = (Y - Y.mean())/np.std(Y)
# 对数据进行分割
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.7, random_state=1)
# 创建pca模型
pca = PCA(n_components='mle')
# 对模型进行训练
pca.fit(X_train)
# 返回降维后据
X_train = pca.transform(X_train)# 使用返回后的数据用线性回归模型进行建模
import statsmodels.api as sm
ols = sm.OLS(Y_train, X_train).fit()
ols.summary()
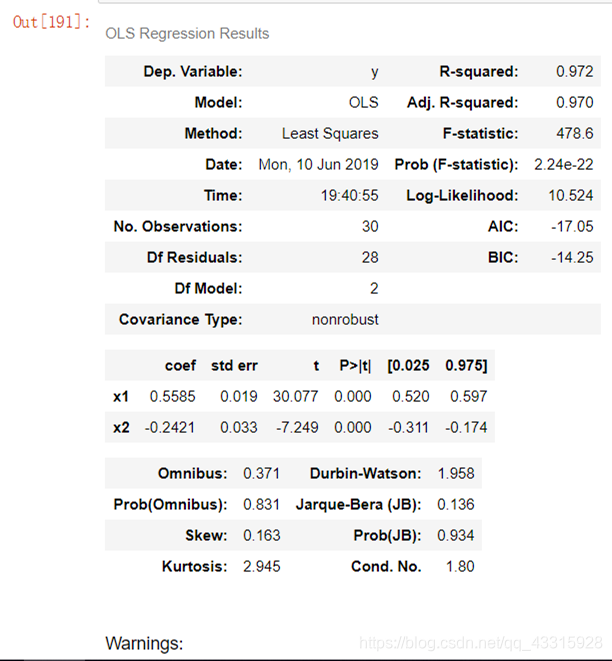
由图片可以看到,ols回归后的R^2 是0.972, p值很小,说明模型拟合的很好。
# 使用LinearRegression进行拟合,其实这两种拟合的都差不多
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train,Y_train) # 模型训练
lr.score(X_train, Y_train) # 获取模型的得分
输出结果为:
0.9715782626501834
对X_test 进行预测
y_pred = lr.predict(X_test)
建立线性模型并查看y_pred与y_test的R^2
olsr = sm.OLS(y_pred, Y_test).fit()
olsr.summary()
输出的结果显示为:0.877
说明预测的效果还不错,但是如果想要得到更高的预测效果,就需要再从其他方面想想原因了。如:指标是否齐全,模型是否合理,数据是否由缺失,缺失数据的处理方法等。
完整的代码已经上传到:github:https://github.com/DDchenyidi
参考文献:
scikit-learn官网:https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html
sklearn中PCA的使用方法:https://www.jianshu.com/p/8642d5ea5389