Abstract

相比于图像分类而言，目标检测器更加复杂，具有多个损失函数。而目前的的检测中，其主要将注意力集中在对象的区域中，但本文指出，从背景中提取的特征信息对于学生模型的学习也是必不可少的。且由于目标区域和背景区域包含的信息不同，所以所授予的权重也应该时不同的。在此基础上，本文提出了一种新的基于解耦特征的蒸馏算法DeFeat，性能有所提升，

1. Introduction

先介绍了为了提升目标检测的准确性，计算资源成本的增加和检测速度的明显降低。解决方法有：量化、剪枝、网络设计和知识蒸馏等。接下来介绍了几个基于知识蒸馏的目标检测算法，FGFI让学生网络学习教师网络目标的附近锚定位置；TADF通过颈部特征中的高斯mask对对象区域和检测头中的正样本作为学生网络学习对象。但这些方法仅从目标区域提取知识，忽略背景。

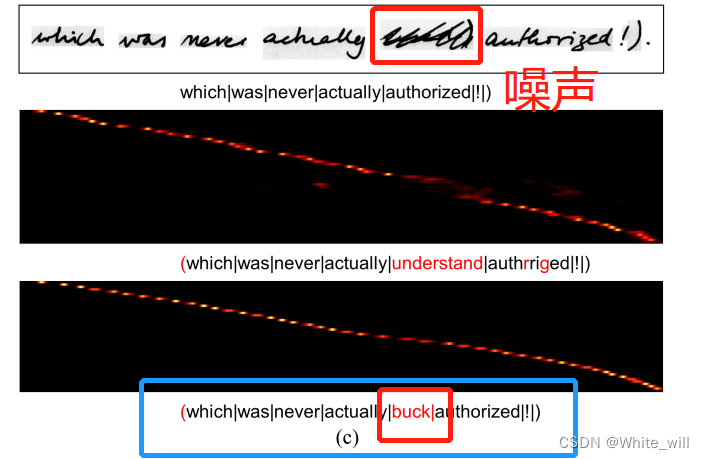
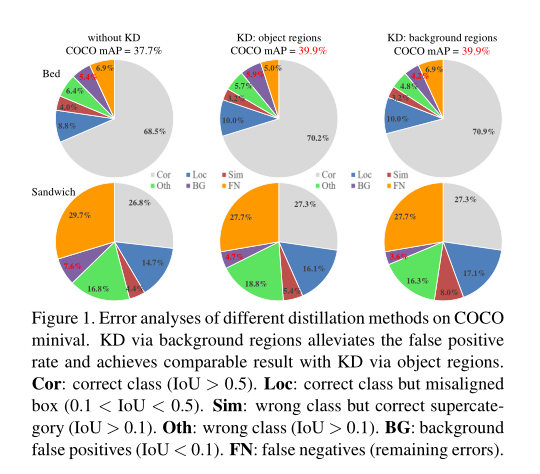
通过实验可知，即仅通过背景区域特征提取学生也可以显著提高学生的学习能力，甚至可以获得与通过目标区域提取学生相类似的结果（如下图）。

之前的文献也有表明，物体和背景之间有很强的关系，对象可能性$P(O|V_o,V_b)=P(O|V_b)\frac{P(V_o|O,V_b)}{P(V_o|V_b)}$ 。其中，$V_o,V_b$表示目标特征和背景特征，通过公式可知，所有的概率都与背景信息有关。同时，通过观察以前的论文可知：目标区域和背景区域都可以通过蒸馏独立地受益于目标检测，但一旦集成在一起，性能会下降。

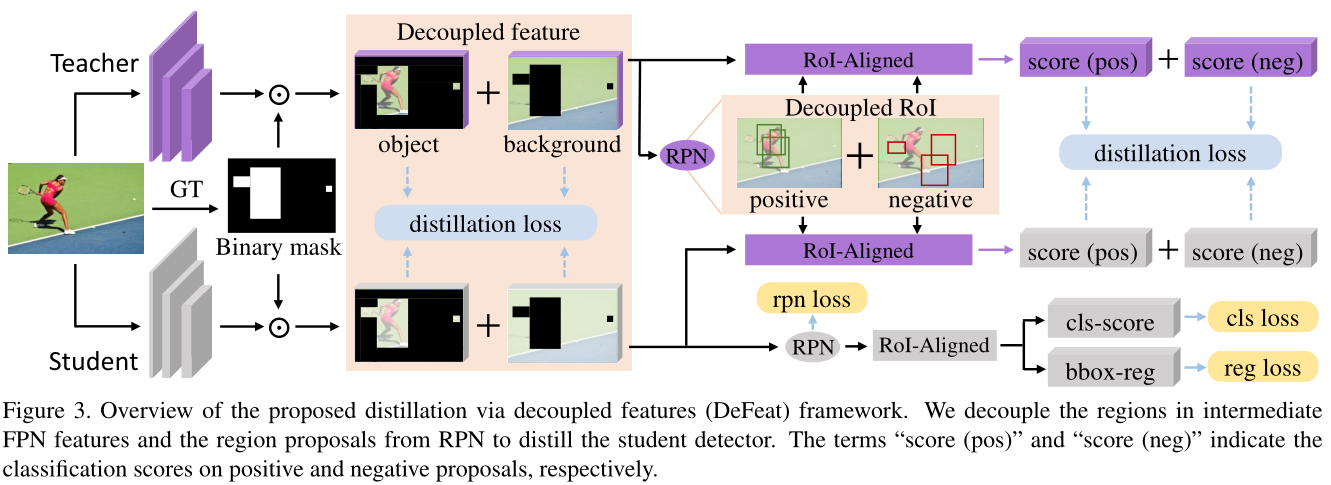
基于上述分析，提出将知识蒸馏的特征解耦，并分别赋予不同的重要性，包含两个阶段的特征：即FPN特征和ROI-Aligned特征。使用 ground-truth mask将FPN特征分割成目标和背景，并在教师和学生之间使用均方误差损失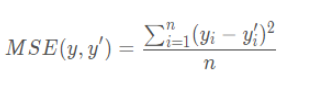：ROI-Aligned特征也被分为pos和neg部分，基于这些解耦的RoI-Aligned特征生成的分类分数是使用KL散度损失来得到的。

2. Related Work

综上所述，现有的目标检测提取框架忽略了背景区域在中间特征中的重要作用和分类头中的负区域proposal（但对整个特征映射的模拟和分类头中的提取都忽略了前景和背景的不平衡，这可能导致次优结果）。

3. Distillation via Decoupled Features

一般来说，目标检测器由三到四个部分组成：1）backbone-用于提取特征 2）neck-融合多层特征 3）RPN-用于生成proposals 4）开始对象分类和边界看回归。蒸馏的目的是让学生网络学习教师网络的知识，可以是中间层特征或分类头中的propos的软预测。

定义$S\in R^{H\times W\times C}和T\in R^{H\times W\times C}$分别为学生和教师的中间特征。通过中间特征进行蒸馏的表述为：
$$L_{fea}=\frac{\gamma }{2N}\sum _{h=1}^H\sum _{w=1}^W\sum _{c=1}^{C}I(\varphi (S_{h,w,c})-T_{h,w,c}{)}^2$$
其中$N=HWC$是元素总数 ， $\gamma$为蒸馏损失的调节系数， $\varphi$表示适应层， $I$表示掩膜。

对RPN输出的K个区域的proposals， 分类头需要计算所有proposals的软标签。通过软标签预测的蒸馏可表述为：
$$L_{cls}=\frac{1}{K}\sum _{i=1}^K{L}_{CE}(y_i^s,Y_i)+\frac{\lambda }{K}\sum _{i=1}^K{L}_{KL}(y_i^s,y_i^t)$$
超参数$\lambda$用来平衡不同的损失，$L_{CE}$和$L_{KL}$分别表示交叉熵损失和KL散度损失，$Y_i$表示真实值，$y_i^s,y_i^t$分别表示

学生预测标签和老师预测标签。学生网络的整体损失为：
$$L=L_{fea}+L_{cls}+L_{reg}+L_{rpn}$$
$L_{reg}$ 是边界盒回归损失， $L_{rpn}$是RPN损失

3.1 Decouple Intermediate Features in Distillation

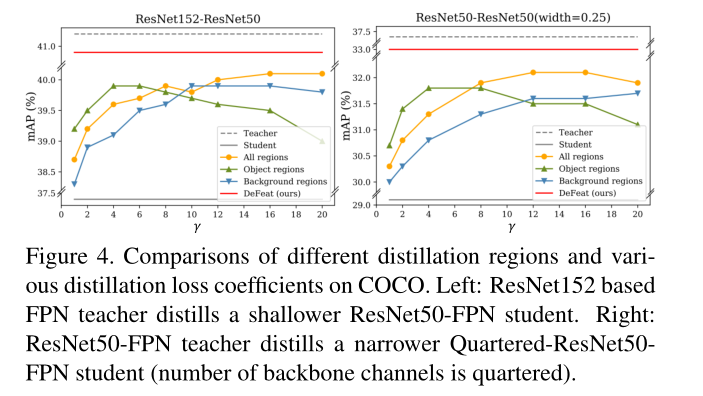
如下图所示。，仅通过背景区域的蒸馏仍然可以获得与仅通过对象区域的蒸馏相当的结果， 因此中间特征中的背景区域可以补充目标区域，进一步帮助学生检测器的训练。问题是如何在蒸馏过程中适当的整合这两类区域。

基于以上观察，通过解耦特征提取学生。对于尺寸为$H\times W$的特征， 首先我们根据ground-truth生成一个二值掩码M：
$$M_{i,j}=1[(i,j)\in B]$$
其中 M ∈ { 0 , 1 } H × W M ∈ \{0, 1\}^{H×W} M∈{0,1}H×W，如果$(i,j)$属于对象，则$M=1$，否则为0。如果detector包含可以输出多层特征的FPN，就将每个ground-truth分配到相应级别，然后分别生成掩码M。最后使用生成的二进制掩码来解耦颈部特征。

中间特征的蒸馏损失为：
$$L_{fea}=\frac{{\alpha }_{obj}}{2N_{obj}}\sum _{h=1}^H\sum _{w=1}^W\sum _{c=1}^C{M}_{h,w}(\varphi (S_{h,w,c})-T_{h,w,c}{)}^2+\frac{{\alpha }_{bg}}{2N_{bg}}\sum _{h=1}^H\sum _{w=1}^W\sum _{c=1}^C(1-M_{h,w})(\varphi (S_{h,w,c})-T_{h,w,c}{)}^2$$
其中， $N_{obj}=C{\sum }_{h=1}^H{\sum }_{w=1}^W{M}_{w,h}$,，表示目标区域的元素数， $N_{obj}=C{\sum }_{h=1}^H{\sum }_{w=1}^W(1-M_{w,h})$，表示背景元素的个数。${\alpha }_{obj},{\alpha }_{bg}$分别表示目标区域和背景区域的系数

3.2. Decouple Region Proposals in Distillation

目标对象(positive)的蒸馏损失始终大于背景(negative)的蒸馏损失.如果不平衡两者，则背景proposals产生的小梯度会淹没在positive proposas的大梯度中，从而限制进一步细化。因此，我们建议在提取分类头时，将区域建议解耦为正（对象）propoals和负（背景）proposals，以达到最佳收敛。我们将教师检测器生成的区域建议输入教师和学生的头部，以生成类别预测$p_t$和$p_s$，positive proposal和negative proposal分别处理，如下图所示：

对于positive proposals的概率$z$，使用温度$T_{obj}$来软化（这是温度为T的softmax）：
$$p^{s,T_{obj}}(c|{\theta }^s)=\frac{exp(z_c^s/T_{obj})}{{\sum }_{j=1}^{C}exp(z_j^s/T_{obj})}c\in Y$$

$$p^{t,T_{obj}}(c|{\theta }^t)=\frac{exp(z_c^t/T_{obj})}{{\sum }_{j=1}^{C}exp(z_j^t/T_{obj})}c\in Y$$

其中，${\theta }^s$和${\theta }^t$分别表示教师学生网络和教师网络的参数， Y = { 1 , 2 , . . . , C } Y = \{1, 2, ..., C\} Y={1,2,...,C}是类别。

为了从教师中提取学生的知识，使用了KL散度：
$$L_{cls}=\frac{{\beta }_{obj}}{K_{obj}}\sum _{i=1}^K{b}_i{L}_{KL}(p_i^{s,T_{obj}},p_i^{t,T_{obj}})+\frac{{\beta }_{bg}}{K_{bg}}\sum _{i=1}^K(1-b_i)L_{KL}(p_i^{s,T_{bg}},p_i^{t,T_{bg}})$$

$$L_{KL}(p^{s,T},p^{t,T})=T^2\sum _{c=1}^C{p}^{t,T}(c|{\theta }^t)log\frac{p^{t,T}(c|{\theta }_t)}{p^{s,T}(c|{\theta }^s)}$$

其中，$b_i$表示真实对象的第i个标签，${\beta }_{obj}$和${\beta }_{bg}$表示阳性和阴性的系数，$K_{obj}={\sum }_i{b}_i$和$K_{bg}={\sum }_i(1-b_i)$表示positive proposals和negative proposals的数量。$T^2$用来保证梯度大小的比例。

4. Experiments