本文来自2022年CVPR的文章，论文地址点这里

一. 介绍

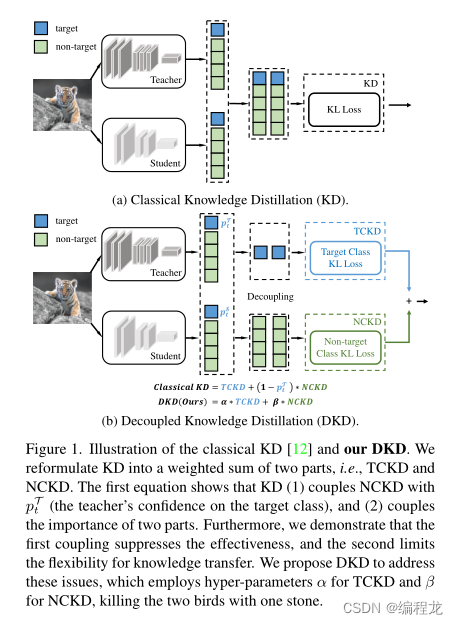
知识蒸馏（KD）的通过最小化师生预测对数之间的KL-Divergence来传递知识(下图a)。目前大部分的研究注意力都被吸引到从中间层的深层特征中提取知识。与基于logit的精馏方法相比，特征精馏在各种任务中都具有优越的性能，因此对logit精馏的研究很少。然而，基于特征的方法的训练成本并不令人满意，因为在训练期间，为了提取深度特征，引入了额外的计算和存储使用(例如，网络模块和复杂的操作)。
Logit蒸馏需要边际计算和存储成本，但性能较差。直观地说，logit蒸馏应该达到与特征蒸馏相当的性能，因为logit比深层特征具有更高的语义级别。我们认为，由于未知的原因限制了logit蒸馏的潜力，导致其性能不理想。为了重振基于逻辑的方法，我们从深入研究KD机制开始这项工作。首先，我们将分类预测分为两个层次:(1)对目标类和所有非目标类的二元预测和(2)对每个非目标类的多类预测。在此基础上，我们将经典的KD损失重新表述为两部分，如下图b所示。一种是针对目标类的二元logit蒸馏，另一种是针对非目标类的多类logit蒸馏。为简化起见，我们将其分别命名为目标分类知识蒸馏(TCKD)和非目标分类知识蒸馏(NCKD)。重新构建知识蒸馏的损失计算使我们能够独立地研究这两个部分的影响。

二. 方法

2.1 重新定义KD

定义。 对于一个第$t$个类别的训练样本，分类的概率可以表示为$\mathbf{p}=$ $\left[p_1,p_2,\dots ,p_t,\dots ,p_C\right]\in {\mathbb{R}}^{1\times C}$，其中$p_i$表示为第$i$个类，$C$表示为所有类别的数量。每一个$\mathbf{p}$可以使用softmax函数进行计算：
$$p_i=\frac{\exp \left(z_i\right)}{{\sum }_{j=1}^C\exp \left(z_j\right)},\text{\hspace{1em}(1)}$$
其中$z_i$表示第$i$个类的逻辑输出。
为了区分与目标类相关和不相关的部分，我们定义接下来的部分。$\mathbf{b}=\left[p_t,p_{\backslash t}\right]\in {\mathbb{R}}^{1\times 2}$，计算过程如下：
$$p_t=\frac{\exp \left(z_t\right)}{{\sum }_{j=1}^C\exp \left(z_j\right)},p_{\backslash t}=\frac{{\sum }_{k=1,k\ne t}^C\exp \left(z_k\right)}{{\sum }_{j=1}^C\exp \left(z_j\right)}.$$
同时，我们定义$\hat{\mathbf{p}}=\left[{\hat{p}}_1,\dots ,{\hat{p}}_{t-1},{\hat{p}}_{t+1},\dots ,{\hat{p}}_C\right]\in$ ${\mathbb{R}}^{1\times (C-1)}$ 表示为非目标类的概率分，其中对于每一个元素计算如下：
$${\hat{p}}_i=\frac{\exp \left(z_i\right)}{{\sum }_{j=1,j\ne t}^C\exp \left(z_j\right)}.\text{\hspace{1em}(2)}$$
重新构建。 我们使用$\mathcal{T}$以及$\mathcal{S}$表示为教师和学生网络模型。那么，经典的知识蒸馏使用KL三度去计算损失如下：
$$\begin{array}{rl}\mathrm{KD}& =\mathrm{KL}\left({\mathbf{p}}^{\mathcal{T}}\Vert {\mathbf{p}}^{\mathcal{S}}\right)\\ & =p_t^{\mathcal{T}}\log \left(\frac{p_t^{\mathcal{T}}}{p_t^S}\right)+\sum _{i=1,i\ne t}^C{p}_i^{\mathcal{T}}\log \left(\frac{p_i^{\mathcal{T}}}{p_i^{\mathcal{S}}}\right).\end{array}\text{\hspace{1em}(3)}$$
接下来，我们使用式子(1)(2)带入到式子(3):
$$\begin{array}{rl}\mathrm{KD}& =p_t^{\mathcal{T}}\log \left(\frac{p_t^{\mathcal{T}}}{p_t^S}\right)+\sum _{i=1,i\ne t}^C{p}_{\backslash t}^{\mathcal{T}}{\hat{p}}_i^{\mathcal{T}}\log \left(\frac{p_{\backslash t}^{\mathcal{T}}{\hat{p}}_i^{\mathcal{T}}}{p_{\backslash \backslash }^{\mathcal{S}}{\hat{p}}_i^S}\right)\\ & =p_t^{\mathcal{T}}\log \left(\frac{p_t^{\mathcal{T}}}{p_t^S}\right)+\sum _{i=1,i\ne t}^C{p}_{\backslash t}^{\mathcal{T}}{\hat{p}}_i^{\mathcal{T}}\left(\log \left(\frac{{\hat{p}}_i^{\mathcal{T}}}{{\hat{p}}_i^{\mathcal{S}}}\right)+\log \left(\frac{p_{\backslash t}^{\mathcal{T}}}{p_{\backslash t}^S}\right)\right)\\ & =p_t^{\mathcal{T}}\log \left(\frac{p_t^{\mathcal{T}}}{p_t^S}\right)+\sum _{i=1,i\ne t}^C{p}_{\backslash t}^{\mathcal{T}}{\hat{p}}_i^{\mathcal{T}}\log \left(\frac{{\hat{p}}_i^{\mathcal{T}}}{{\hat{p}}_i^S}\right)\\ & +\sum _{i=1,i\ne t}^C{p}_{\backslash t}^{\mathcal{T}}{\hat{p}}_i^{\mathcal{T}}\log \left(\frac{p_{\backslash t}^{\mathcal{T}}}{p_{\backslash t}^S}\right)\end{array}$$
其中$p_{\backslash t}^{\mathcal{T}}$以及$p_{\backslash t}^{\mathcal{S}}$表示为类$i$的不相关的部分，有:
$$\begin{array}{rl}\sum _{i=1,i\ne t}^C{p}_{\backslash t}^{\mathcal{T}}{\hat{p}}_i^{\mathcal{T}}\log \left(\frac{p_{\backslash t}^{\mathcal{T}}}{p_{\backslash t}^{\mathcal{S}}}\right)& =p_{\backslash t}^{\mathcal{T}}\log \left(\frac{p_{\backslash t}^{\mathcal{T}}}{p_{\backslash t}^{\mathcal{S}}}\right)\sum _{i=1,i\ne t}^C{\hat{p}}_i^{\mathcal{T}}\\ & =p_{\backslash t}^{\mathcal{T}}\log \left(\frac{p_{\backslash t}^{\mathcal{T}}}{p_{\backslash t}^{\mathcal{S}}}\right)\end{array}$$
因此，可以得到
$$\begin{array}{rl}\mathrm{KD}& =p_t^{\mathcal{T}}\log \left(\frac{p_t^{\mathcal{T}}}{p_t^S}\right)+p_{\backslash t}^{\mathcal{T}}\sum _{i=1,i\ne t}^C{\hat{p}}_i^{\mathcal{T}}\left(\log \left(\frac{{\hat{p}}_i^{\mathcal{T}}}{{\hat{p}}_i^S}\right)+\log \left(\frac{p_{\backslash t}^{\mathcal{T}}}{p_{\backslash t}^S}\right)\right)\\ & =\underset{\mathrm{KL}\left({\mathbf{b}}^{\mathcal{T}}\Vert {\mathbf{b}}^{\mathcal{S}}\right)}{\underbrace{p_t^{\mathcal{T}}\log \left(\frac{p_t^{\mathcal{T}}}{p_t^S}\right)+p_{\backslash t}^{\mathcal{T}}\log \left(\frac{p_{⟨t}^{\mathcal{T}}}{p_{\backslash t}^S}\right)}}+p_{\backslash t}^{\mathcal{T}}\underset{\mathrm{KL}\left({\hat{\mathbf{p}}}^{\mathcal{T}}\Vert {\hat{\mathbf{p}}}^{\mathcal{S}}\right)}{\underbrace{\sum _{i=1,i\ne t}^C{\hat{p}}_i^{\mathcal{T}}\log \left(\frac{{\hat{p}}_i^{\mathcal{T}}}{{\hat{p}}_i^S}\right)}}.\end{array}\text{\hspace{1em}(4)}$$
之后，我们将式子(4)改写为：
$$\mathrm{KD}=\mathrm{KL}\left({\mathbf{b}}^{\mathcal{T}}\Vert {\mathbf{b}}^{\mathcal{S}}\right)+\left(1-p_t^{\mathcal{T}}\right)\mathrm{KL}\left({\hat{\mathbf{p}}}^{\mathcal{T}}\Vert {\hat{\mathbf{p}}}^{\mathcal{S}}\right)\text{\hspace{1em}(5)}$$
根据式子(5)我们可以或的两个部分：$\mathrm{KL}\left({\mathbf{b}}^{\mathcal{T}}\Vert {\mathbf{b}}^{\mathcal{S}}\right)$表示为教师以及学生的目标类的相似程度。因此我们可以命名其为目标类的知识蒸馏(TCKD)。同时$\mathrm{KL}\left({\hat{\mathbf{p}}}^{\mathcal{T}}\Vert {\hat{\mathbf{p}}}^{\mathcal{S}}\right)$表示为非目标类的学生模型和教师模型的相似程度。因此，我们可以进一步将式子(5)改写为：
$$\mathrm{KD}=\mathrm{TCKD}+\left(1-p_t^{\mathcal{T}}\right)\mathrm{NCKD}.\text{\hspace{1em}(6)}$$

2.2 TCKD以及NCKD的影响

这部分大概描写的是作者做的哪些实验去验证这两部分，这里我就不在去解释一次。简单来说，对于TCKD来说，它传递了样本难度的相关知识，也就是训练样本的难度越大，TCKD体现出来的效果越好。而NCKD则是逻辑蒸馏的主要挑战，可以发现当教师网络预测目标类越精准的时候，NCKD的系数反而越小，则导致其没有起到良好的训练作用，影响了良好的知识传递。

2.3 分解的知识蒸馏(DKD)

根据上面进行分析的，我们可以重新设置我们需要的知识蒸馏的超参数，如下：
$$\mathrm{DKD}=\alpha \mathrm{TCKD}+\beta \mathrm{NCKD}.\text{\hspace{1em}(7)}$$
具体的算法如下：

三. 代码解析

代码链接点这里

""" 
logits_student : 学生网络的逻辑输出
logits_teacher ： 教师网络的逻辑输出
target ：标签值
alpha、beta、temperature : 超参数
"""
def dkd_loss(logits_student, logits_teacher, target, alpha, beta, temperature):### 获得每个target值对应的掩码，从而获得p_tgt_mask = _get_gt_mask(logits_student, target)### 获得其他target对应的掩码，从而获得p_{\t}other_mask = _get_other_mask(logits_student, target)pred_student = F.softmax(logits_student / temperature, dim=1)pred_teacher = F.softmax(logits_teacher / temperature, dim=1)## 计算b^T以及b^Spred_student = cat_mask(pred_student, gt_mask, other_mask)pred_teacher = cat_mask(pred_teacher, gt_mask, other_mask)log_pred_student = torch.log(pred_student)tckd_loss = (F.kl_div(log_pred_student, pred_teacher, size_average=False)* (temperature**2)/ target.shape[0])pred_teacher_part2 = F.softmax(logits_teacher / temperature - 1000.0 * gt_mask, dim=1)log_pred_student_part2 = F.log_softmax(logits_student / temperature - 1000.0 * gt_mask, dim=1)nckd_loss = (F.kl_div(log_pred_student_part2, pred_teacher_part2, size_average=False)* (temperature**2)/ target.shape[0])return alpha * tckd_loss + beta * nckd_loss

四. 总结

其实本文的想法很简单，但却从数学的角度分析了逻辑知识蒸馏效果不如特征知识蒸馏的原因，并且设置了详细的实验去验证了分解后的知识蒸馏。