Decoupled network
https://zhuanlan.zhihu.com/p/37598903
神经网络机制存在的缺陷?
过拟合,梯度消失或者是膨胀,训练依靠大量样本,对网络初始化及其敏感记忆协迁移等等。
Decupled network是对operator的改进
现在的卷积操作就是一个內积操作
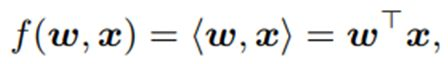
矩阵相乘计算,两个矩阵相似度的操作(类似卷积滤波)。
解耦操作,是什么内容的耦合?简单来讲是类内差异和类间差异的耦合。也就是说卷积操作得到的结果很相似的时候,并不能得到一个结论说这两个很相似,反之亦不能。因为你不能够区别这种差异或者相似度是类内差异造成的还是类间的差异造成的(而对于分类的问题来讲,我们其实关心的就是类间差异而已)。

这张图是 CNN在手写体识别任务上学到的特征的2D可视化示意图。 0~9每一个手写体数字对应的特征是图中的一束;任意一束当中的不同位置表示的是同一类别的不同表征,也就是类间差距(intra-class Variations);束与束之间形成的夹角表达的是两个类别之间的差距(inter-class difference),也就是这里所谓的语义差异。
不解耦会存在什么问题呢?
就是说你只能得到一个最终的结果,但是对于两个同样的输出,你不能分辨造成这个结果的原因是因为他们实际就是同一种类别,还是刚好ab=cd
![]()
直接将卷积操作解耦为幅值和角度两个部分,并且将这两个部分分别用两个函数表示h()和g().
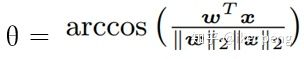
角度函数g()则度量着不同的类别之间的差异,关于幅值的函数h()则度量同一类别中的差异,同时其值的大小也就表示这个类别的可信度。
传统的卷积操作就变成了解耦网络的一个特例:
![]()
为什么角度可以来衡量类别之间的差异呢?
作者是从傅里叶变换当中的得到的motivation: 对于傅里叶变换来说,两个概念非常的重要,一个就是幅值,另一个就是相位。对于一张图像的傅里叶变换,如果你使用幅值和随机的相位重建这张图像,得到的结果往往不能辨认;但是如果你使用相位和随机的幅值却能够重建出能够辨认的图像。
讨论两个函数的设计:包括有界的,无界的;加权的不加权的以及解耦网络的集合解释等等。
h(||w||,||x||)
- ShereCov
- BallCov
- TanhConv

g()是一个关于ϴ的函数,大多实际上是一个非线性的函数,也就是其实就是一个激活函数,这里作者称之为角度激活函数(Angular activation)
Linear:
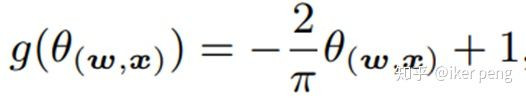
Cosine:
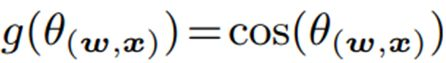
实验部分,比较了设计DN网络的收敛性,非线性,BN功能,而且和ResNet进行了对比。

这个表格中,每一行都是一个卷积操作子也就是h()Norm函数,每一列都是一个角度激活函数g(),如之前所说,对于一个一般CNN就是g()=Cosine
操作子的非线性的比较
加relu
目标识别性能比较
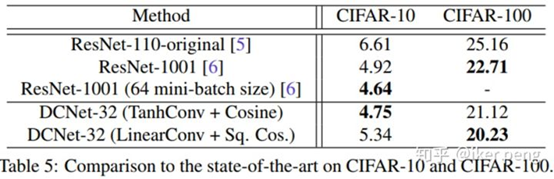
损失函数设计上见到使用模长和夹角来分离变量扩大类间差别
学习目标loss和神经网络结构function class很有可能是耦合的,对于不同的loss,最优的网络结构很可能是不同的,在dcnet里面,很可能对于不同的loss,最优的g和h也是不同的,这么说来,dcnet里面的learnable g和learnable h就可能更加有用了。
解耦网络
基于內积的卷积一直是卷积神经网络的核心组成部分,也是学习视觉特征的关键。CNN学习到的特征可以自然的解耦为:特征的模对应类内的变化,特征的角度对应语义差异,受到这个观察的启发。提出一种通用的解耦学习框架,其分别模拟了类内变化和语义差异。具体来讲,首先将內积重新参数化为解耦形式,然后将其推广到解耦卷积运算符,该运算符用作解耦网络的构件块。基于解耦运算符,我们进一步提出从数据中直接学习运算符。大量实验表明,这种解耦重新参数化可以显著提高性能,并且收敛更容易,鲁棒性更强。