一、题目

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

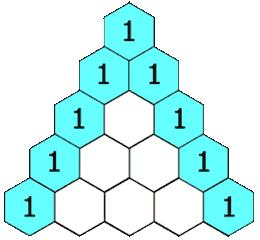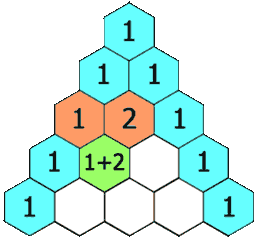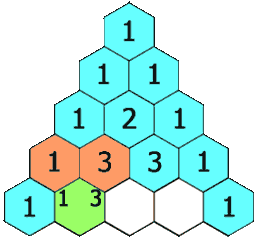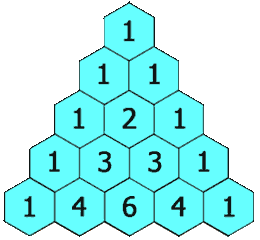
在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 5
输出:
[[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]
]

二、解题思路

本题本质上是一个动态规划题，杨辉三角需要用前一行的值来构造后一行的值，思路很简单，主要是找规律。

首先我们先考虑三种特殊情况：

分别是numRows等于0，1和2

其次考虑numRows >=3的情况，也就是每行首尾的值都为1，中间值是：
$$a[i][j]=a[i-1][j-1]+a[i-1][j]$$

三、三种解题示例

1、常规方法

class Solution:def generate(self, numRows: int) -> List[List[int]]:nums = []for row_num in range(numRows):Row = [1 for _ in range(row_num+1)]for i in range(1, len(Row)-1):Row[i] = nums[row_num-1][i-1] + nums[row_num-1][i]nums.append(Row) return nums

2、递归方法

class Solution:def generate(self, numRows: int) -> List[List[int]]:if numRows == 0: return [] # 等于0情况if numRows == 1: return [[1]] # 等于1情况s = self.generate(numRows-1) # 递归调用s.append([1] + [s[-1][i-1]+s[-1][i] for i in range(1,len(s))] + [1])return s

3、动态规划

class Solution:def generate(self, numRows: int) -> List[List[int]]:nums = [[1]*(i + 1) for i in range(numRows)] # 列表推导式生成储存1的列表n = 2 while n < numRows: # 从第三行开始遍历每一行for i in range(1, len(nums[n]) - 1): nums[n][i] = nums[n - 1][i - 1] + nums[n - 1][i]n += 1 return nums