原地址https://artrajz.cn/index.php/archives/32/

前言

其实道题在寒假的时候就做了，现在有机会发出来了。(〃‘▽’〃)

题目

思路

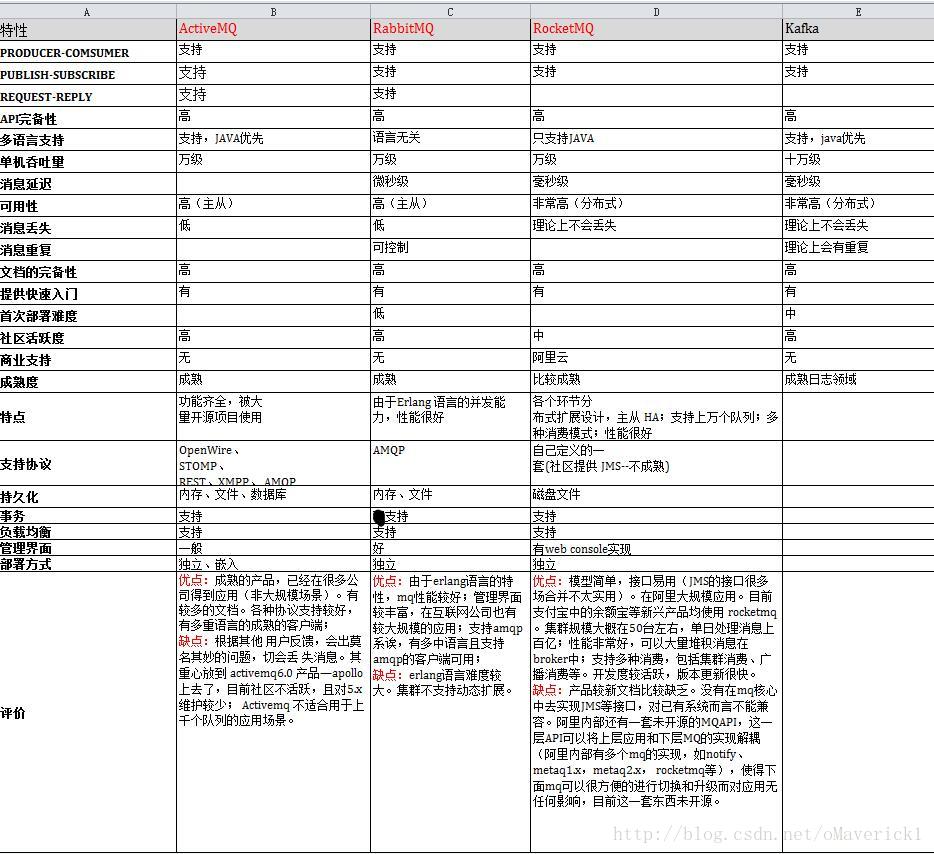
参考了大佬斜行查找的思路，为了便于观察和叙述，我把杨辉三角形如图排一下

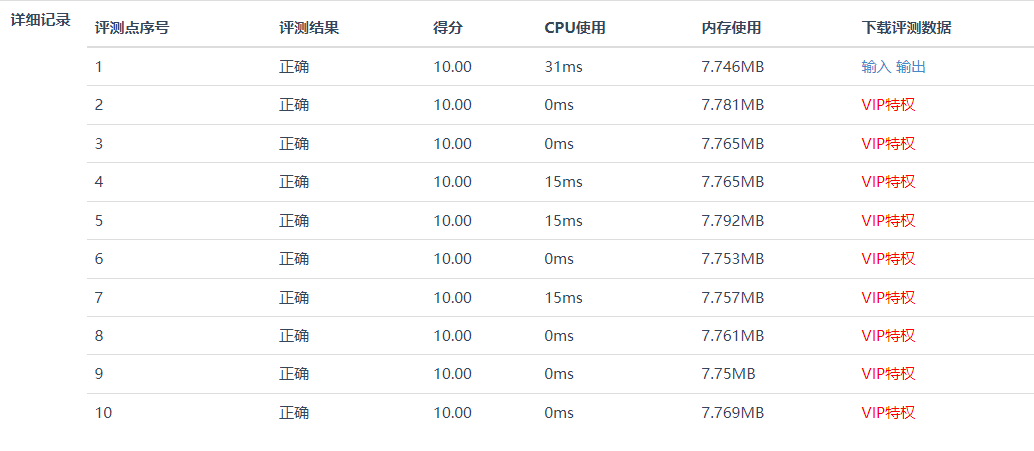
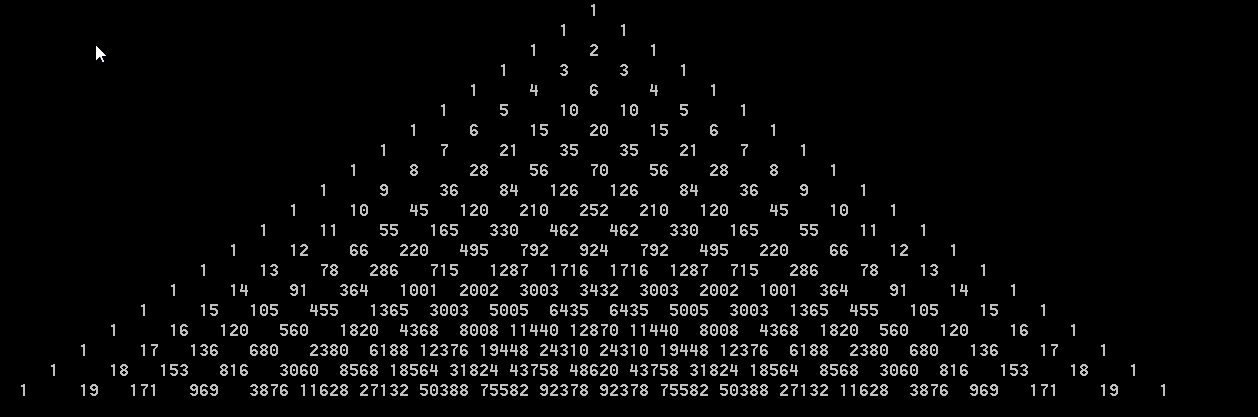
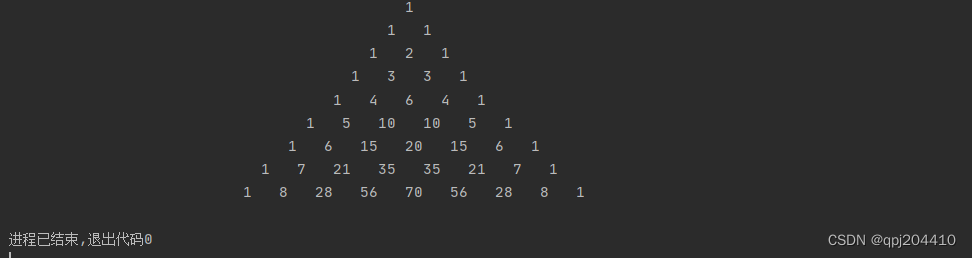
  1 1   1 1   2   1 1   3   3   1 1   4   6   4   1 1   5  10  10   5   1 1   6  15  20  15   6   1 1   7  21  35  35  21   7   1 1   8  28  56  70  56  28   8   1 1   9  36  84 126 126  84  36   9   1 1  10  45 120 210 252 210 120  45  10   1 

从图形上看，第一列全都是1，显然没什么查询的价值，省略。。

每一行的第一个也都是1，也没什么价值，省略。。

通过观察发现，每个奇数行中间的数都是最大的，也是第一次出现的。也就是说从(1,2)开始每次坐标(+1,+2)上的数都是最早出现的，比如说2,6,20,70…

利用这个规律，我们先找到离要查找的数最近的那一列（差的绝对值最小 and 小于等于）

我们可以从2这个数的坐标(1,2)开始查找每一列最接近要查找的数的值，比如要查找21，我们先利用上面那个规律查找

首先21>2，坐标(+1,+2)来到(2,4)；

21>6，坐标(+1,+2)来到(3,6)；

21>20，坐标(+1,+2)来到(4,8)；

21<70，不移动坐标了，锁定20这个数的坐标。

然后在20这一列(3,*)开始查找21,用二分查找的方法提高速度。突然发现在这一列中找不到21，只能将坐标往前移动一列来到15这个位置。

为什么不往后移动而是往前移动呢？是因为杨辉三角形的对称的特点，往后找虽然可能找得到，但是一定不是最早出现的。

往前移动一列后，再次利用二分查找，发现找到了21，而且这 个21的位置一定是最早出现的。

我这里用排列组合的方法求杨辉三角，就不用每次都把一个完整的杨辉三角计算出来了,最后再用坐标求位置

题解

import sys
n = int(input())
t = 1#n为1直接出结果
if n == 1:print(1)sys.exit()#先找到是哪一列比较接近
l = 0   #行
r = 0   #列
while t < n:t = 1l += 2r += 1for i in range(l-r+1,l+1):#排列组合求杨辉三角t *= ifor i in range(2,r+1):t //= i
##        print(t)if t == n:print(l*(l+1)//2+r+1)sys.exit()
else:l -= 2r -= 1t = 1#再用二分法在竖列中查找
j = l
k = n
while t != n:l = (j+k)//2t = 1for i in range(l-r+1,l+1):#排列组合求杨辉三角t *= ifor i in range(2,r+1):t //= iif j < k:   #二分查找if t > n:k = l - 1elif t < n:j = l + 1elif t == n:    #找到就退出，以免坐标错乱break;else:   #这里是该列找不到，就往前一列找r -= 1k = n
##        print(t)print(l*(l+1)//2+r+1)   #利用坐标求位置