戳气球和布尔运算问题（巨难）

一.大气球的最大得分

1.对应letecode链接

打气球的最大分数_牛客题霸_牛客网 (nowcoder.com)

2.题目描述：

3.解题思路

本题个人觉得本题巨难：主要步骤如下：

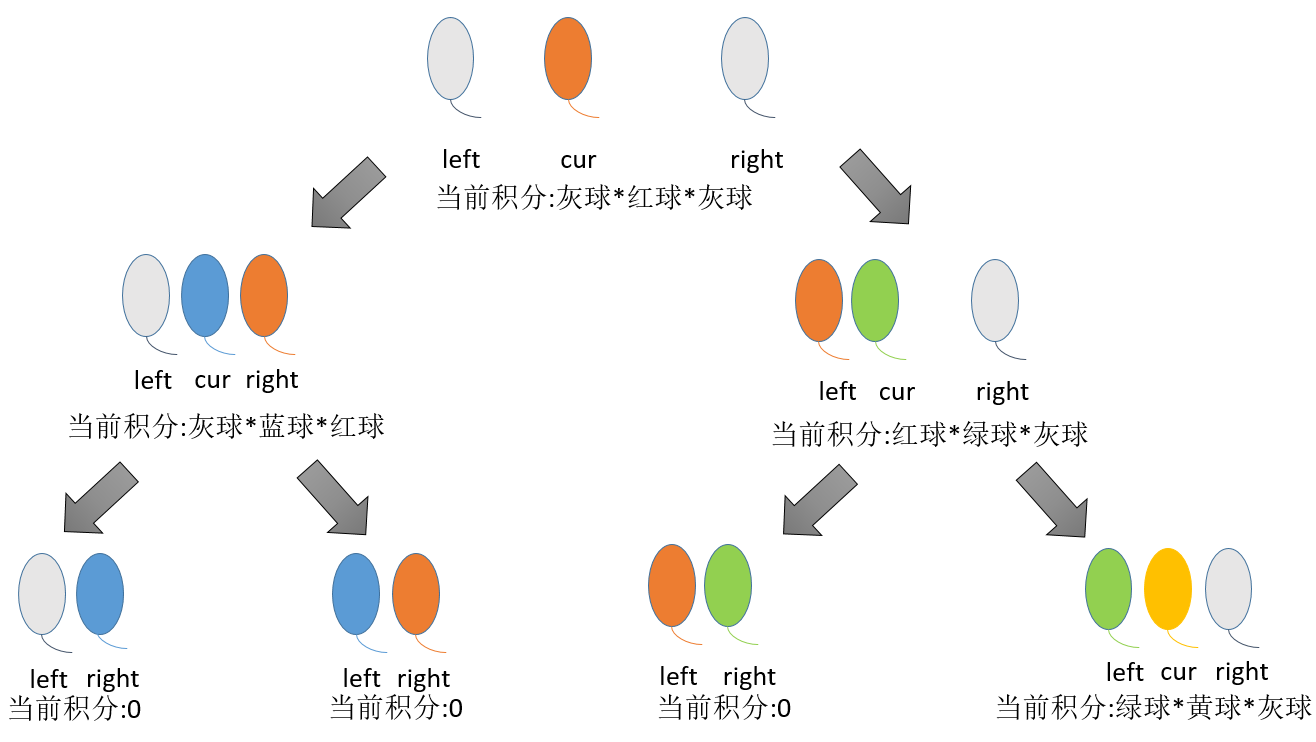
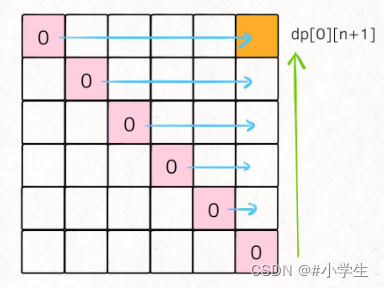
1.预处理：为便于处理，可在 nums 数组两端各添加一个哨兵 1，即nums[0]=和nums[N]=1,其中N为数组的长度。

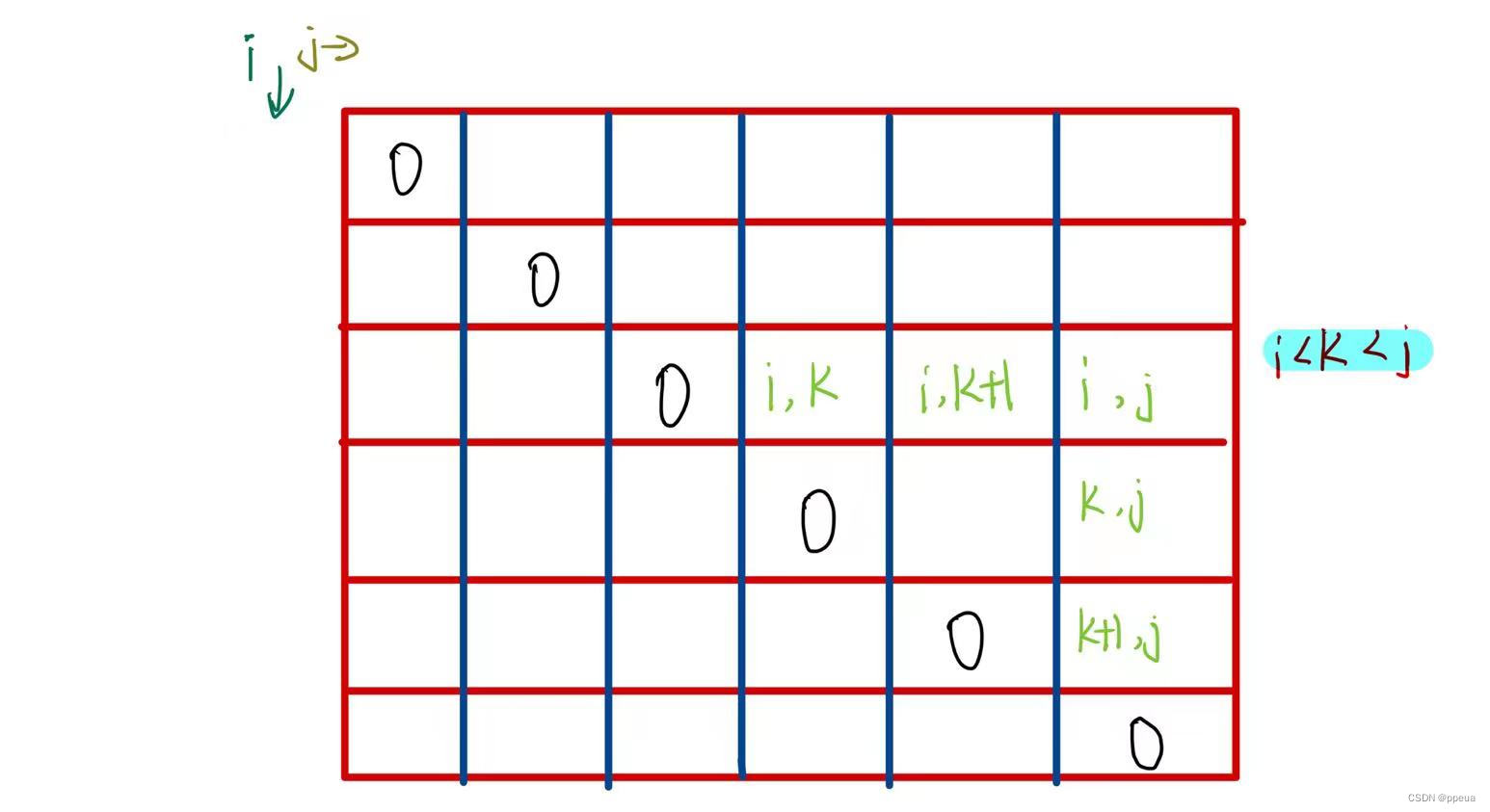
2.定义递归函数func（vector<int>&nums,int L,int R)其递归含义为nums[L........R]范围内能获得的最大得分

3.我们发现我们在尝试可能性时对应每个位置的得分和它左边的状态和右边的状态都有关这使得尝试的可能性非常的多所以。我们可以这样尝试，我们尝试每个废物最后打爆能获得的最大得分。

4.注意：递归函数func必须保证一个潜台词nums[L-1]位置的数必须没爆并且nums[R+1]位置的数也没爆必须遵守否则就别调这个函数

首先在一头一尾添加一个1，这个是为了方便代码实现。下面我们可以产生可能性

我们尝试cur位置最后被打爆注意：（如果一个区间为（left,right)那么这个区间里面一个气球也没有）。我们每个位置都这样尝试最后答案一定就在其中我们只需要进行更新即可。

4.对应代码：

#include<iostream>
#include<vector>
using namespace std;
//潜台次arr[L-1]位置和arr[R+1]位置一定没爆
//递归含义arr[L.....R]范围内的最大得分
int func(vector<int>& arr, int L, int R) {if (L == R) { //只有一个气球打爆即可return arr[L] * arr[L - 1] * arr[R + 1];}//可能性1：最后打爆arr[L]位置的气球int p1 = func(arr, L + 1, R) + arr[L] * arr[L - 1] * arr[R + 1];//可能性2：最后打爆arr[R]位置的气球int p2 = func(arr, L, R - 1) + arr[R] * arr[L - 1] * arr[R + 1];int ans = max(p1, p2);for (int i = L + 1; i < R; i++) {//产生[L+1,R-1]范围内每个位置最后打爆能获得的最大得分int left = func(arr, L, i - 1); //打爆左边部分int right = func(arr, i + 1, R); //打爆右边部分int cur = arr[i] * arr[L - 1] * arr[R + 1]; //打爆当前位置ans = max(ans, cur + left + right);//更新答案}return ans;
}
int maxCoins(vector<int>& nums) {int N = nums.size();vector<int>arr(N + 2);for (int i = 0; i < N; i++) {arr[i + 1] = nums[i];}arr[0] = arr[N + 1] = 1;dp.resize(N + 1, vector<int>(N + 1, -1));return func(arr, 1, N);
}int main() {int N;cin >> N;vector<int>arr(N);for (int i = 0; i < N; i++) {cin >> arr[i];}cout << maxCoins(arr) << endl;return 0;
}

2.记忆化搜索代码：

#include<iostream>
#include<vector>
using namespace std;
vector<vector<int>>dp;
//潜台次arr[L-1]位置和arr[R+1]位置一定没爆
//递归含义arr[L.....R]范围内的最大得分
int func(vector<int>& arr, int L, int R) {if (L == R) { //只有一个气球打爆即可return arr[L] * arr[L - 1] * arr[R + 1];}if (dp[L][R] != -1) {return dp[L][R];}//可能性1：最后打爆arr[L]位置的气球int p1 = func(arr, L + 1, R) + arr[L] * arr[L - 1] * arr[R + 1];//可能性2：最后打爆arr[R]位置的气球int p2 = func(arr, L, R - 1) + arr[R] * arr[L - 1] * arr[R + 1];int ans = max(p1, p2);for (int i = L + 1; i < R;i++) {//产生[L+1,R-1]范围内每个位置最后打爆能获得的最大得分int left = func(arr, L, i - 1); //打爆左边部分int right = func(arr, i + 1, R); //打爆右边部分int cur = arr[i] * arr[L - 1] * arr[R + 1]; //打爆当前位置ans = max(ans, cur + left + right);//更新答案}dp[L][R] = ans;return ans;
}
int maxCoins(vector<int>& nums) {if (nums.size() == 0) {return 0;}int N = nums.size();vector<int>arr(N + 2);for (int i = 0; i < N; i++) {arr[i + 1] = nums[i];}arr[0] = arr[N + 1] = 1;dp.resize(N + 1, vector<int>(N + 1, -1));return func(arr, 1, N);
}int main() {int N;cin >> N;vector<int>arr(N);for (int i = 0; i < N; i++) {cin >> arr[i];}dp.resize(N + 1, vector<int>(N + 1, -1));cout << maxCoins(arr) << endl;return 0;
}

严格位置依赖的动态规划：

#include<iostream>
#include<vector>
using namespace std;int maxCoins(vector<int>& nums) {if (nums.size() == 0) {return 0;}int N = nums.size();vector<int>arr(N + 2);for (int i = 0; i < N; i++) {arr[i + 1] = nums[i];}arr[0] = arr[N + 1] = 1;vector<vector<int>>dp(N + 2, vector<int>(N + 2));for (int i = 1; i <= N; i++) {dp[i][i] = arr[i] * arr[i - 1] * arr[i + 1];}for (int L = N; L >= 1; L--) {for (int R = L + 1; R <= N; R++) {int ans = max(arr[L - 1] * arr[L] * arr[R + 1] + dp[L + 1][R],arr[L - 1] * arr[R] * arr[R + 1] + dp[L][R - 1]);for (int i = L + 1; i < R; i++) {int left = dp[L][i - 1];int right = dp[i + 1][R];int cur = arr[i] * arr[L - 1] * arr[R + 1];ans = max(ans, left + right + cur);}dp[L][R] = ans;}}return dp[1][N];}int main() {int N;cin >> N;vector<int>arr(N);for (int i = 0; i < N; i++) {cin >> arr[i];}cout << maxCoins(arr) << endl;return 0;
}

二.布尔运算

1.对应letecode链接

面试题 08.14. 布尔运算 - 力扣（LeetCode）

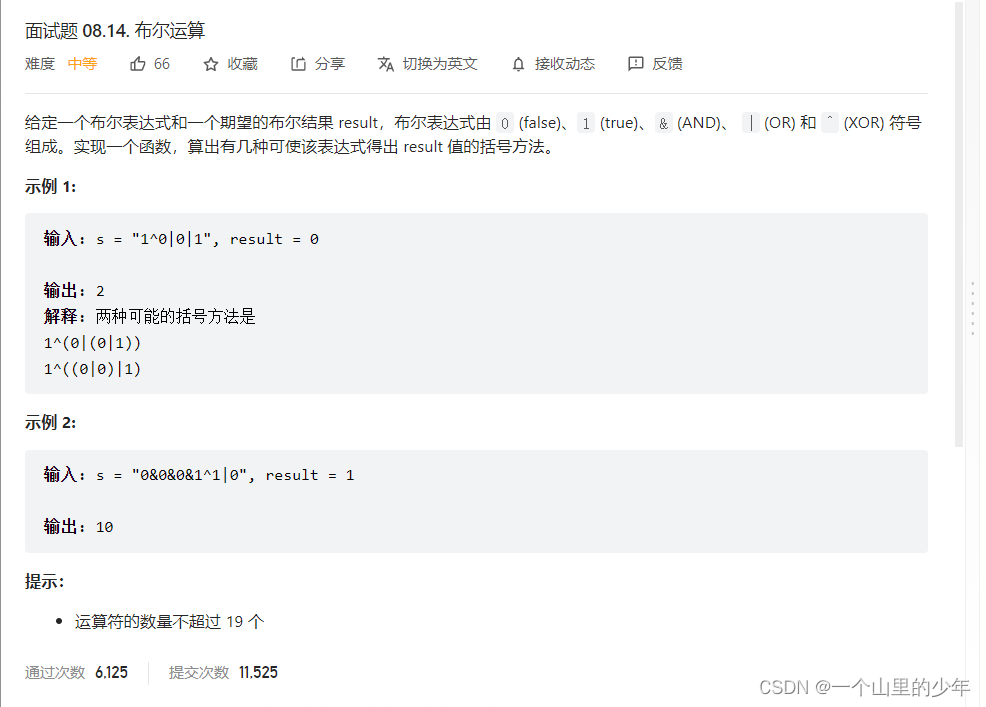
2.题目描述：

3.解题思路：

1.尝试每个符号最后进行计算能够得到的true或者false的方法数。

2.定义递归函数Info*func(str,L,R)的含义为str从[L......R]范围内为true和false的方法数。并且L和R位置非0就是1，具体请看代码

4.对应代码

class Solution {public:struct Info {Info(int tr, int tf) {t = tr;f = tf;}int t;//t代表为true的方法数int f;//代表为false的方法数};int countEval(string s, int result) {dp.resize(s.size(), vector<Info*>(s.size(), NULL));Info* ret = func(s, 0, s.size() - 1);return result == 1 ? ret->t : ret->f;}//L......R上必须L和R非0就是1Info* func(const string& str, int L, int R) {int t = 0;int f = 0;if (L == R) {t = str[L] == '1' ? 1 : 0;f = str[L] == '0' ? 1 : 0;}else {//注意一定要保存递归的潜台词L和R位置非0即1for (int Split = L + 1; Split < R;Split += 2) { //尝试每个符号最后进行运算能够得到结果的方法数Info* leftInfo = func(str, L, Split - 1);Info* rightInfo = func(str, Split + 1, R);int a = leftInfo->t;int b = leftInfo->f;int c = rightInfo->t;int d = rightInfo->f;switch (str[Split]) { //根据最后算的这个符号进行分类计算case'&':t += a * c;f += b * c + b * d + a * d;break;case'|':t += a * c + a * d + b * c;f += b * d;break;case '^':t += a * d + b * c;f += a * c + b * d;break;}}}Info* ans = new Info(t, f);return ans;}};

记忆化搜索：

class Solution {public:struct Info {Info(int tr, int tf) {t = tr;f = tf;}int t;int f;};vector<vector<Info*>>dp;int countEval(string s, int result) {dp.resize(s.size(), vector<Info*>(s.size(), NULL));Info* ret = func(s, 0, s.size() - 1);return result == 1 ? ret->t : ret->f;}//L......R上必须L和R非0就是1Info* func(const string& str, int L, int R) {if (dp[L][R]) {return dp[L][R];}int t = 0;int f = 0;if (L == R) {t = str[L] == '1' ? 1 : 0;f = str[L] == '0' ? 1 : 0;}else {cout << L << " " << R << endl;for (int Split = L + 1; Split < R; Split += 2) {Info* leftInfo = func(str, L, Split - 1);Info* rightInfo = func(str, Split + 1, R);int a = leftInfo->t;int b = leftInfo->f;int c = rightInfo->t;int d = rightInfo->f;switch (str[Split]) {case'&':t += a * c;f += b * c + b * d + a * d;break;case'|':t += a * c + a * d + b * c;f += b * d;break;case '^':t += a * d + b * c;f += a * c + b * d;break;}}}Info* ans = new Info(t, f);dp[L][R] = ans;return ans;}};