点击上方蓝字设为星标
东哥带你手把手撕力扣~
作者:labuladong
公众号:labuladong
若已授权白名单也必须保留以上来源信息
今天我们要聊的这道题「Burst Balloon」和之前我们写过的那篇 经典动态规划:高楼扔鸡蛋问题 分析过的高楼扔鸡蛋问题类似,知名度很高,但难度确实也很大。因此 labuladong 公众号就给这道题赐个座,来看一看这道题目到底有多难。
它是 LeetCode 第 312 题,题目如下:
首先必须要说明,这个题目的状态转移方程真的比较巧妙,所以说如果你看了题目之后完全没有思路恰恰是正常的。虽然最优答案不容易想出来,但基本的思路分析是我们应该力求做到的。所以本文会先分析一下常规思路,然后再引入动态规划解法。
一、回溯思路
先来顺一下解决这种问题的套路:
我们前文多次强调过,很显然只要涉及求最值,没有任何奇技淫巧,一定是穷举所有可能的结果,然后对比得出最值。
所以说,只要遇到求最值的算法问题,首先要思考的就是:如何穷举出所有可能的结果?
穷举主要有两种算法,就是回溯算法和动态规划,前者就是暴力穷举,而后者是根据状态转移方程推导「状态」。
如何将我们的扎气球问题转化成回溯算法呢?这个应该不难想到的,我们其实就是想穷举戳气球的顺序,不同的戳气球顺序可能得到不同的分数,我们需要把所有可能的分数中最高的那个找出来,对吧。
那么,这不就是一个「全排列」问题嘛,我们前文 回溯算法框架套路详解 中有全排列算法的详解和代码,其实只要稍微改一下逻辑即可,伪码思路如下:
int res = Integer.MIN_VALUE;
/* 输入一组气球,返回戳破它们获得的最大分数 */
int maxCoins(int[] nums) {backtrack(nums, 0);return res;
}
/* 回溯算法的伪码解法 */
void backtrack(int[] nums, int socre) {if (nums 为空) {res = max(res, score);return;}for (int i = 0; i < nums.length; i++) {int point = nums[i-1] * nums[i] * nums[i+1];int temp = nums[i];// 做选择在 nums 中删除元素 nums[i]// 递归回溯backtrack(nums, score + point);// 撤销选择将 temp 还原到 nums[i]}
}
回溯算法就是这么简单粗暴,但是相应的,算法的效率非常低。这个解法等同于全排列,所以时间复杂度是阶乘级别,非常高,题目说了nums的大小n最多为 500,所以回溯算法肯定是不能通过所有测试用例的。
二、动态规划思路
这个动态规划问题和我们之前的动态规划系列文章相比有什么特别之处?为什么它比较难呢?
原因在于,这个问题中我们每戳破一个气球nums[i],得到的分数和该气球相邻的气球nums[i-1]和nums[i+1]是有相关性的。
我们前文 动态规划套路框架详解 说过运用动态规划算法的一个重要条件:子问题必须独立。所以对于这个戳气球问题,如果想用动态规划,必须巧妙地定义dp数组的含义,避免子问题产生相关性,才能推出合理的状态转移方程。
如何定义dp数组呢,这里需要对问题进行一个简单地转化。题目说可以认为nums[-1] = nums[n] = 1,那么我们先直接把这两个边界加进去,形成一个新的数组points:
int maxCoins(int[] nums) {int n = nums.length;// 两端加入两个虚拟气球int[] points = new int[n + 2];points[0] = points[n + 1] = 1;for (int i = 1; i <= n; i++) {points[i] = nums[i - 1];}// ...
}
现在气球的索引变成了从1到n,points[0]和points[n+1]可以认为是两个「虚拟气球」。
那么我们可以改变问题:在一排气球points中,请你戳破气球0和气球n+1之间的所有气球(不包括0和n+1),使得最终只剩下气球0和气球n+1两个气球,最多能够得到多少分?
现在可以定义dp数组的含义:
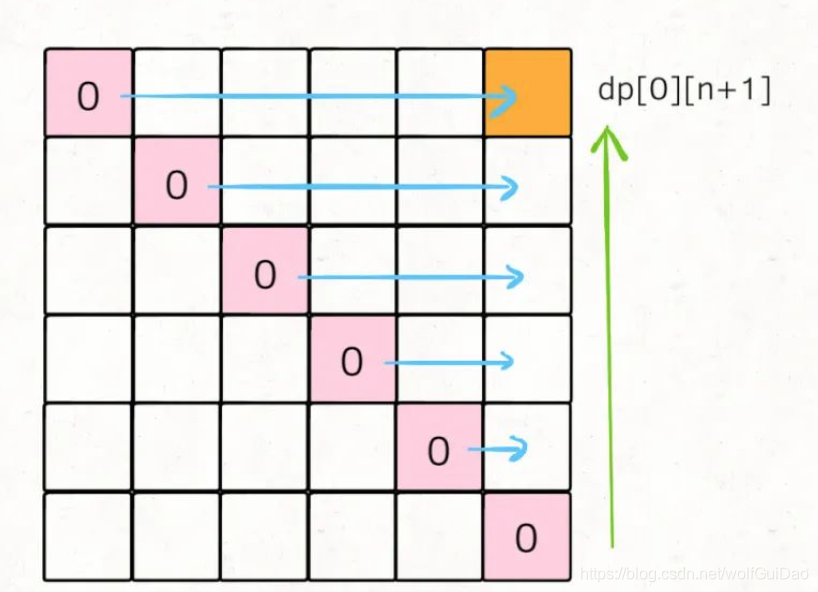
dp[i][j] = x表示,戳破气球i和气球j之间(开区间,不包括i和j)的所有气球,可以获得的最高分数为x。
那么根据这个定义,题目要求的结果就是dp[0][n+1]的值,而 base case 就是dp[i][j] = 0,其中0 <= i <= n+1, j <= i+1,因为这种情况下,开区间(i, j)中间根本没有气球可以戳。
// base case 已经都被初始化为 0
int[][] dp = new int[n + 2][n + 2];
现在我们要根据这个dp数组来推导状态转移方程了,根据我们前文的套路,所谓的推导「状态转移方程」,实际上就是在思考怎么「做选择」,也就是这道题目最有技巧的部分:
不就是想求戳破气球i和气球j之间的最高分数吗,如果「正向思考」,就只能写出前文的回溯算法;我们需要「反向思考」,想一想气球i和气球j之间最后一个被戳破的气球可能是哪一个?
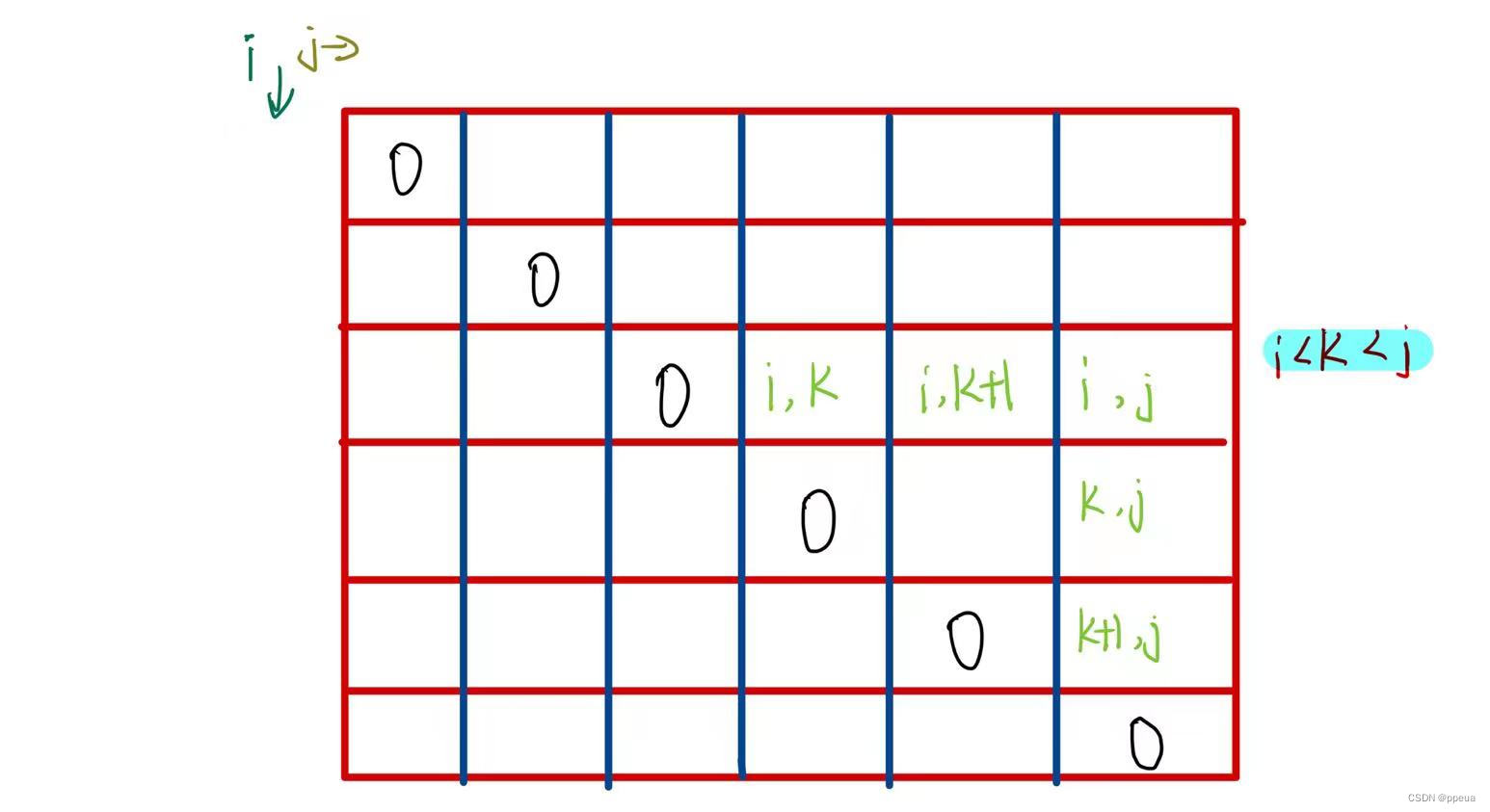
其实气球i和气球j之间的所有气球都可能是最后被戳破的那一个,不防假设为k。回顾动态规划的套路,这里其实已经找到了「状态」和「选择」:i和j就是两个「状态」,最后戳破的那个气球k就是「选择」。
根据刚才对dp数组的定义,如果最后一个戳破气球k,dp[i][j]的值应该为:
dp[i][j] = dp[i][k] + dp[k][j] + points[i]*points[k]*points[j]
你不是要最后戳破气球k吗?那得先把开区间(i, k)的气球都戳破,再把开区间(k, j)的气球都戳破;最后剩下的气球k,相邻的就是气球i和气球j,这时候戳破k的话得到的分数就是points[i]*points[k]*points[j]。
那么戳破开区间(i, k)和开区间(k, j)的气球最多能得到的分数是多少呢?嘿嘿,就是dp[i][k]和dp[k][j],这恰好就是我们对dp数组的定义嘛!
结合这个图,就能体会出dp数组定义的巧妙了。由于是开区间,dp[i][k]和dp[k][j]不会影响气球k;而戳破气球k时,旁边相邻的就是气球i和气球j了,最后还会剩下气球i和气球j,这也恰好满足了dp数组开区间的定义。
那么,对于一组给定的i和j,我们只要穷举i < k < j的所有气球k,选择得分最高的作为dp[i][j]的值即可,这也就是状态转移方程:
// 最后戳破的气球是哪个?
for (int k = i + 1; k < j; k++) {// 择优做选择,使得 dp[i][j] 最大dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[k][j] + points[i]*points[j]*points[k]);
}
写出状态转移方程就完成这道题的一大半了,但是还有问题:对于k的穷举仅仅是在做「选择」,但是应该如何穷举「状态」i和j呢?
for (int i = ...; ; )for (int j = ...; ; )for (int k = i + 1; k < j; k++) {dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[k][j] + points[i]*points[j]*points[k]);
return dp[0][n+1];
三、写出代码
关于「状态」的穷举,最重要的一点就是:状态转移所依赖的状态必须被提前计算出来。
拿这道题举例,dp[i][j]所依赖的状态是dp[i][k]和dp[k][j],那么我们必须保证:在计算dp[i][j]时,dp[i][k]和dp[k][j]已经被计算出来了(其中i < k < j)。
那么应该如何安排i和j的遍历顺序,来提供上述的保证呢?我们前文 动态规划答疑篇 写过处理这种问题的一个鸡贼技巧:根据 base case 和最终状态进行推导。
PS:最终状态就是指题目要求的结果,对于这道题目也就是dp[0][n+1]。
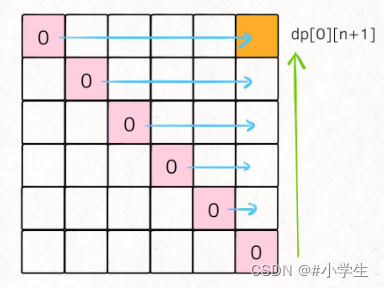
我们先把 base case 和最终的状态在 DP table 上画出来:
对于任一dp[i][j],我们希望所有dp[i][k]和dp[k][j]已经被计算,画在图上就是这种情况:
那么,为了达到这个要求,可以有两种遍历方法,要么斜着遍历,要么从下到上从左到右遍历:
斜着遍历有一点难写,所以一般我们就从下往上遍历,下面看完整代码:
int maxCoins(int[] nums) {int n = nums.length;// 添加两侧的虚拟气球int[] points = new int[n + 2];points[0] = points[n + 1] = 1;for (int i = 1; i <= n; i++) {points[i] = nums[i - 1];}// base case 已经都被初始化为 0int[][] dp = new int[n + 2][n + 2];// 开始状态转移// i 应该从下往上for (int i = n; i >= 0; i--) {// j 应该从左往右for (int j = i + 1; j < n + 2; j++) {// 最后戳破的气球是哪个?for (int k = i + 1; k < j; k++) {// 择优做选择dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[k][j] + points[i]*points[j]*points[k]);}}}return dp[0][n + 1];
}
至此,这道题目就完全解决了,十分巧妙,但也不是那么难,对吧?
关键在于dp数组的定义,需要避免子问题互相影响,所以我们反向思考,将dp[i][j]的定义设为开区间,考虑最后戳破的气球是哪一个,以此构建了状态转移方程。
对于如何穷举「状态」,我们使用了小技巧,通过 base case 和最终状态推导出i,j的遍历方向,保证正确的状态转移。
往期推荐 ????
数据结构和算法学习指南
我作了首诗,保你闭着眼睛也能写对二分查找
回溯算法解题框架
动态规划解题框架
经动态规划:编辑距离
动态规划之博弈问题
动态规划之KMP算法详解
_____________
公众号:labuladong
B站:labuladong
知乎:labuladong
fucking-algorithm 项目在 Github 上已破 39k star,即将出版,公众号后台回复关键词「pdf」限时免费下载,回复「进群」可加入刷题群。东哥手把手带你撕 LeetCode,感受支配算法的快感~