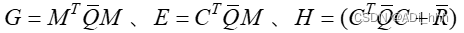MPC基本概念
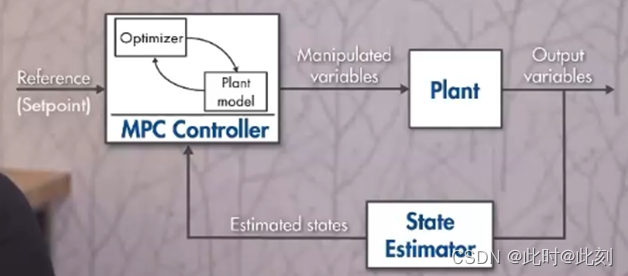
模型预测控制(MPC)是指通过模型来预测系统在某一未来时间段内的表现来进行优化控制。MPC多用于数位控制,因此使用系统的离散型状态空间表达形式,即 x k + 1 = A x k + B u k x_{k+1}=Ax_k+Bu_k xk+1=Axk+Buk。MPC一般分为3步:
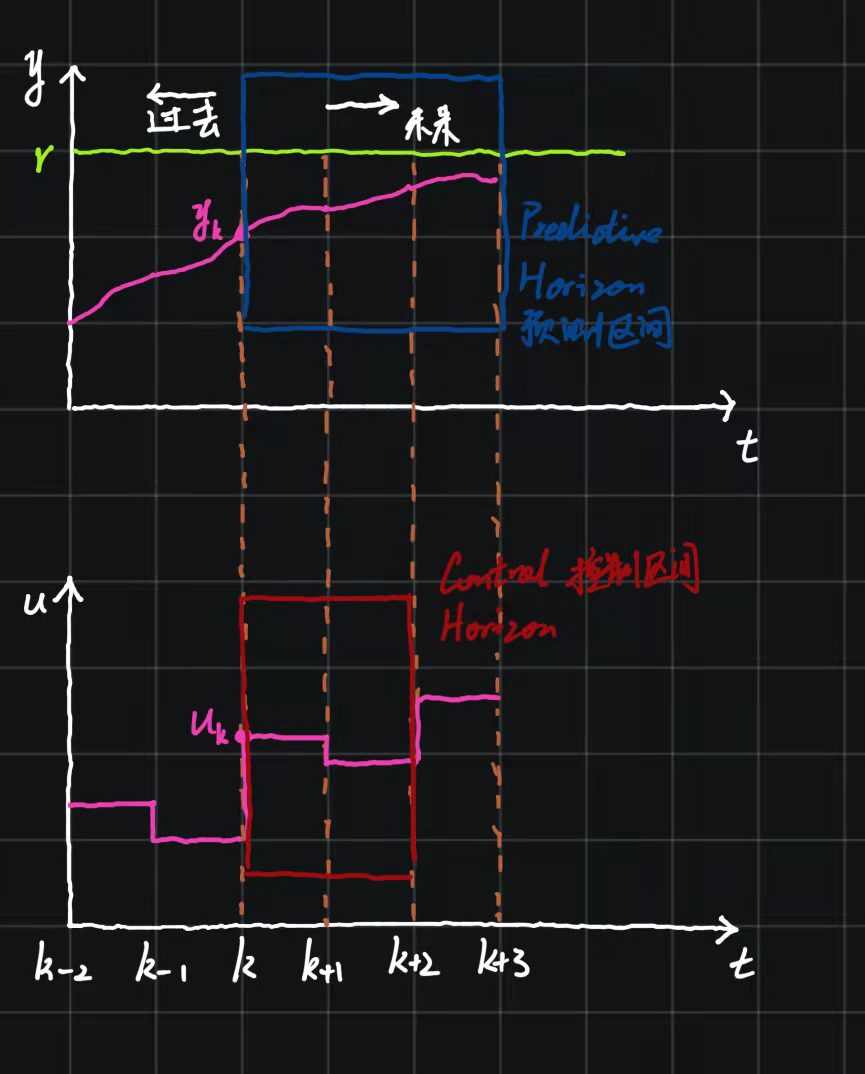
- 估计/测量读取当前的系统状态;
- 基于 u k u_k uk、 u k + 1 u_{k+1} uk+1、……、 u k + n u_{k+n} uk+n来进行最优化;
- 只取 k k k时刻的系统输入 u k u_k uk,在 k + 1 k+1 k+1时刻,将控制区间(Control Horizon)和预测区间(Predictive Horizon)右移,重新执行前两步。
这个过程被称为滚动优化控制(Receding Horizon Control)。代价函数(Cost Function)为
J = ∑ k N − 1 ( E k T Q E k + u k T R u k + E N T F E N ) J=\sum^{N-1}_k(E^T_kQE_k+u_k^TRu_k+E_N^TFE_N) J=k∑N−1(EkTQEk+ukTRuk+ENTFEN)
其中 E N E_N EN为最终误差(Terminal Error)。MPC在求解时会考虑系统的约束(Constrains)。
最优化建模
对于MPC,有很多方法可以对其最优化,这里介绍二次规划(Quadratic Programming)方法。二次规划的一般形式为求 Z T Q Z + C T Z Z^TQZ+C^TZ ZTQZ+CTZ的最小值,在这个式子里,第一项是二次型,第二项是线性的。如果 Q Q Q是一个对角阵,这个式子就变成了一个最小二乘的问题。
建立二次规划模型
对于一个系统 x ( k + 1 ) = A x ( k ) + B u ( k ) x(k+1)=Ax(k)+Bu(k) x(k+1)=Ax(k)+Bu(k),其中 X X X为状态向量, U U U为系统输入。在 k k k时刻估计的系统在 k k k时刻的输入为 u ( k ∣ k ) u(k|k) u(k∣k),在k时刻估计的系统在 k + i k+i k+i时刻的输入为 u ( k + i ∣ k ) u(k+i|k) u(k+i∣k),直到 u ( k + N − 1 ∣ k ) u(k+N-1|k) u(k+N−1∣k), k k k到 k + N − 1 k+N-1 k+N−1为预测区间。对于系统状态也是同样,从 x ( k ∣ k ) x(k|k) x(k∣k)到 x ( k + N ∣ k ) x(k+N|k) x(k+N∣k),控制区间比预测区间多一个周期。定义
X k = [ x ( k ∣ k ) x ( k + 1 ∣ k ) x ( k + 2 ∣ k ) ⋮ x ( k + N ∣ k ) ] , U k = [ u ( k ∣ k ) u ( k + 1 ∣ k ) u ( k + 2 ∣ k ) ⋮ u ( k + N ∣ k ) ] X_k=\left[\begin{matrix}x(k|k)\\x(k+1|k)\\x(k+2|k)\\\vdots\\x(k+N|k)\end{matrix}\right], U_k=\left[\begin{matrix}u(k|k)\\u(k+1|k)\\u(k+2|k)\\\vdots\\u(k+N|k)\end{matrix}\right] Xk=⎣⎢⎢⎢⎢⎢⎡x(k∣k)x(k+1∣k)x(k+2∣k)⋮x(k+N∣k)⎦⎥⎥⎥⎥⎥⎤,Uk=⎣⎢⎢⎢⎢⎢⎡u(k∣k)u(k+1∣k)u(k+2∣k)⋮u(k+N∣k)⎦⎥⎥⎥⎥⎥⎤
假设系统输出 y = x y=x y=x,系统参考 r = 0 r=0 r=0,则系统误差 e = y − r = x e=y-r=x e=y−r=x,则系统的代价函数为
J = ∑ i = 0 N − 1 [ x ( k + i ∣ k ) T Q x ( k + i ∣ k ) + u ( k + i ∣ k ) T R u ( k + i ∣ k ) + x ( k + N ) T F x ( k + N ) ] J=\sum^{N-1}_{i=0}[x(k+i|k)^TQx(k+i|k)+u(k+i|k)^TRu(k+i|k)+x(k+N)^TFx(k+N)] J=i=0∑N−1[x(k+i∣k)TQx(k+i∣k)+u(k+i∣k)TRu(k+i∣k)+x(k+N)TFx(k+N)]为了简化计算, Q Q Q和 R R R均设为对角矩阵。其中第一项为误差加权和,第二项为输入加权和,第三项为终端误差。
为了将代价函数与二次规划统一,需要将系统状态 x x x转换为系统输入 u u u的函数。
x ( k ∣ k ) = x k x ( k + 1 ∣ k ) = A x ( k ∣ k ) + B u ( k ∣ k ) = A x k + B u ( k ∣ k ) x ( k + 2 ∣ k ) = A x ( k + 1 ∣ k ) + B u ( k + 1 ∣ k ) = A 2 x k + A B u ( k ∣ k ) + B u ( k + 1 ∣ k ) ⋮ x ( k + N ∣ k ) = A N x k + A N − 1 B u ( k ∣ k ) + ⋯ + B u ( k + N − 1 ∣ k ) \begin{aligned} x(k|k) =& x_k\\x(k+1|k) =&Ax(k|k)+Bu(k|k)\\=&Ax_k+Bu(k|k)\\x(k+2|k)=&Ax(k+1|k)+Bu(k+1|k)\\=&A^2x_k+ABu(k|k)+Bu(k+1|k)\\\vdots\\x(k+N|k)=&A^Nx_k+A^{N-1}Bu(k|k)+\dots+Bu(k+N-1|k) \end{aligned} x(k∣k)=x(k+1∣k)==x(k+2∣k)==⋮x(k+N∣k)=xkAx(k∣k)+Bu(k∣k)Axk+Bu(k∣k)Ax(k+1∣k)+Bu(k+1∣k)A2xk+ABu(k∣k)+Bu(k+1∣k)ANxk+AN−1Bu(k∣k)+⋯+Bu(k+N−1∣k)
所以
X k = [ I A A 2 ⋮ A N ] x k + [ 0 0 0 … 0 B 0 0 … 0 A B B 0 … 0 ⋮ ⋮ ⋮ ⋱ ⋮ A N − 1 B A N − 2 B A N − 3 B … B ] [ u ( k ∣ k ) u ( k + 1 ∣ k ) u ( k + 2 ∣ k ) ⋮ u ( k + N − 1 ∣ k ) ] X_k=\left[\begin{matrix}I\\A\\A^2\\\vdots\\A^N\end{matrix}\right]x_k+\left[\begin{matrix}0&0&0&\dots&0\\B&0&0&\dots&0\\AB&B&0&\dots&0\\\vdots&\vdots&\vdots&\ddots&\vdots\\A^{N-1}B&A^{N-2}B&A^{N-3}B&\dots&B\end{matrix}\right]\left[\begin{matrix}u(k|k)\\u(k+1|k)\\u(k+2|k)\\\vdots\\u(k+N-1|k)\end{matrix}\right] Xk=⎣⎢⎢⎢⎢⎢⎡IAA2⋮AN⎦⎥⎥⎥⎥⎥⎤xk+⎣⎢⎢⎢⎢⎢⎡0BAB⋮AN−1B00B⋮AN−2B000⋮AN−3B………⋱…000⋮B⎦⎥⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎡u(k∣k)u(k+1∣k)u(k+2∣k)⋮u(k+N−1∣k)⎦⎥⎥⎥⎥⎥⎤
即
X k = M x k + C U k X_k=Mx_k+CU_k Xk=Mxk+CUk
回到上面的代价函数,如果我们把第一项和第三项展开,就有
x ( k ∣ k ) T Q x ( k ∣ k ) + x ( k + 1 ∣ k ) T Q x ( k + 1 ∣ k ) + ⋯ + x ( k + N − 1 ∣ k ) T Q x ( k + N − 1 ∣ k ) + x ( k + N ∣ k ) T F x ( k + N ∣ k ) x(k|k)^TQx(k|k)+x(k+1|k)^TQx(k+1|k)+\dots+x(k+N-1|k)^TQx(k+N-1|k)+x(k+N|k)^TFx(k+N|k) x(k∣k)TQx(k∣k)+x(k+1∣k)TQx(k+1∣k)+⋯+x(k+N−1∣k)TQx(k+N−1∣k)+x(k+N∣k)TFx(k+N∣k)
将上式改写为矩阵形式有
原 式 = [ x ( k ∣ k ) x ( k + 1 ∣ k ) x ( k + 2 ∣ k ) ⋮ x ( k + N ∣ k ) ] T [ Q Q Q ⋱ F ] [ x ( k ∣ k ) x ( k + 1 ∣ k ) x ( k + 2 ∣ k ) ⋮ x ( k + N ∣ k ) ] = X T Q ‾ X \begin{aligned} 原式=&\left[\begin{matrix}x(k|k)\\x(k+1|k)\\x(k+2|k)\\\vdots\\x(k+N|k)\end{matrix}\right]^T\left[\begin{matrix}Q&&&&\\&Q&&&\\&&Q&&\\&&&\ddots&\\&&&&F\end{matrix}\right]\left[\begin{matrix}x(k|k)\\x(k+1|k)\\x(k+2|k)\\\vdots\\x(k+N|k)\end{matrix}\right]\\=&X^T\overline{Q}X \end{aligned} 原式==⎣⎢⎢⎢⎢⎢⎡x(k∣k)x(k+1∣k)x(k+2∣k)⋮x(k+N∣k)⎦⎥⎥⎥⎥⎥⎤T⎣⎢⎢⎢⎢⎡QQQ⋱F⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎡x(k∣k)x(k+1∣k)x(k+2∣k)⋮x(k+N∣k)⎦⎥⎥⎥⎥⎥⎤XTQX
同理代价函数的第二项可以化为
原 式 = [ u ( k ∣ k ) u ( k + 1 ∣ k ) u ( k + 2 ∣ k ) ⋮ u ( k + N ∣ k ) ] T [ R R R ⋱ R ] [ u ( k ∣ k ) u ( k + 1 ∣ k ) u ( k + 2 ∣ k ) ⋮ u ( k + N ∣ k ) ] = U T R ‾ U \begin{aligned} 原式=&\left[\begin{matrix}u(k|k)\\u(k+1|k)\\u(k+2|k)\\\vdots\\u(k+N|k)\end{matrix}\right]^T\left[\begin{matrix}R&&&&\\&R&&&\\&&R&&\\&&&\ddots&\\&&&&R\end{matrix}\right]\left[\begin{matrix}u(k|k)\\u(k+1|k)\\u(k+2|k)\\\vdots\\u(k+N|k)\end{matrix}\right]\\=&U^T\overline{R}U \end{aligned} 原式==⎣⎢⎢⎢⎢⎢⎡u(k∣k)u(k+1∣k)u(k+2∣k)⋮u(k+N∣k)⎦⎥⎥⎥⎥⎥⎤T⎣⎢⎢⎢⎢⎡RRR⋱R⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎡u(k∣k)u(k+1∣k)u(k+2∣k)⋮u(k+N∣k)⎦⎥⎥⎥⎥⎥⎤UTRU
代价函数可改写为
J = X k T Q ‾ X k + U k T R ‾ U k = ( M x k + C U k ) T Q ‾ ( M x k + C U k ) + U k T R ‾ U k = ( x k T M T + U k T C T ) Q ‾ ( M x k + C U k ) + U k T R ‾ U k = x k T M T Q ‾ M x k + x k T M T Q ‾ C U k + U k T C T Q ‾ M x k + U k T C T Q ‾ C U k + U k T R ‾ U k = x k T G x k + 2 x k T E U k + U k T H U k \begin{aligned} J=&X^T_k\overline{Q}X_k+U^T_k\overline{R}U_k\\=&(Mx_k+CU_k)^T\overline{Q}(Mx_k+CU_k)+U^T_k\overline{R}U_k\\=&(x^T_kM^T+U^T_kC^T)\overline{Q}(Mx_k+CU_k)+U^T_k\overline{R}U_k\\=&x^T_kM^T\overline{Q}Mx_k+x_k^TM^T\overline{Q}CU_k+U_k^TC^T\overline{Q}Mx_k+U_k^TC^T\overline{Q}CU_k+U_k^T\overline{R}U_k\\=&x_k^TGx_k+2x_k^TEU_k+U_k^THU_k \end{aligned} J=====XkTQXk+UkTRUk(Mxk+CUk)TQ(Mxk+CUk)+UkTRUk(xkTMT+UkTCT)Q(Mxk+CUk)+UkTRUkxkTMTQMxk+xkTMTQCUk+UkTCTQMxk+UkTCTQCUk+UkTRUkxkTGxk+2xkTEUk+UkTHUk
其中 M T Q ‾ M = G M^T\overline{Q}M=G MTQM=G、 M T Q ‾ C = E M^T\overline{Q}C=E MTQC=E、 C T Q ‾ C + R ‾ = H C^T\overline{Q}C+\overline{R}=H CTQC+R=H。上式中第一项只与系统的初始状态有关,是标量;第二项是线性项;第三项是二次项。
本文整理自【MPC模型预测控制器】1_最优化控制和基本概念和MPC模型预测控制器】2_最优化数学建模推导,欢迎大家去关注DR_CAN,他真的好强QAQ。