一、MPC简介
1.1 预测控制的日常应用
模型预测控制的设计目标是计算未来控制变量u的轨迹,以优化未来的系统输出y。优化过程在一个有限的时间窗口进行,并且利用优化时间窗口开始时的系统信息进行优化。为了理解预测控制的基本思想,以一个日常工作为例来进行说明。
工作从上午9点开始,团队的工作目标是完成一个液体容器模型预测控制系统的设计和实现任务。我们会计划好接下来8个小时的工作内容,但是只按照接下来一个小时的计划内容执行,一个小时之后又开始计划接下来8个小时的工作内容,重复这一过程,直到工作完成为止。
在9点这一时刻,计划工作内容的时候,会将9点之前已经完成的工作内容考虑在内。假设工作任务可以分为建模、设计、仿真和实现,那么完成这些任务可以看成是一些列变量的函数,这些变量包括:团队付出的努力程度、团队的工作默契程度、是否有外援帮助等。这些都是规划问题中的可操纵变量(控制变量)。同时团队能力也有局限性,比如理解设计问题的能力、计算机软硬件工程的能力等。这些都是规划问题中的硬约束和软约束。我们已经获取的关于这项工作的背景信息(已完成的工作情况)至关重要。
在考虑了所有事情之后,将接下来8小时的任务定义成可操纵变量的函数。然后,计算出为了完成任务,接下来8小时中每小时所需要的做的事情。在计算中,我们将基于背景信息,考虑到我们自身的局限性作为约束条件,寻找实现目标的最佳途径。得到从上午9点到下午5点的工作计划后,开始执行第一个小时的计划,即9点到10点的工作计划。
在上午10点,需要检查在这一个小时内完成了多少工作。这些信息用于计划我们下一阶段的工作。也许会因为各种原因导致这一小时内没有完成预计的工作。然而,在10点钟,我们对我们所取得的成绩进行了评估,并利用这一最新信息来规划我们接下来8个小时的工作。最终工作目标可能保持不变,也可能会改变。做计划的时间一直是8小时不会改变。重复9点的计划过程,然后给出接下来8小时的新的计划。同样只执行计划中的第一个小时的内容。11点,我们再次评估我们所取得的成绩,并将最新的信息用于接下来8小时的工作计划。计划和实施过程每小时重复一次,直到达到最终的目标。
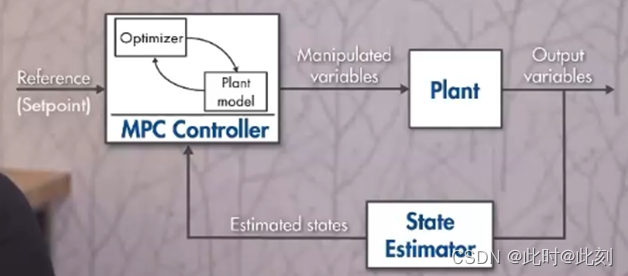
在做计划的过程中,有三点非常关键。第一是要能预测可能发生的事情(也就是要有模型);第二个是能够评估当前的状态和进展(也就是要有测量方法);第三个是要能够实施计划的内容(也就是要实现控制)。规划工作主要包括:
- 规划的时间固定在8个小时;
- 在规划之前需要知道当前的状态;
- 通过考虑约束条件,对8小时的工作采取最佳规划,利用最新的可用信息,在移动的时间窗口进行实时优化。
以上描述的规划活动与MPC的原理相同。在这个例子中,提出了一些概念会经常用到:
- 移动时间窗口:从任意时刻
到
的时间窗口。窗口的长度
是不变的。在本例中每个小时会对接下来8小时的工作进行规划,所以时间窗口长度为
,
是时间窗口的开始点,每小时进行递增,规划从上午9点开始的,所以开始时
。
- 预测时域:规定了希望未来能被预测到多久。这个参数与时间窗口长度
相同。
- 滚动时域控制:虽然未来控制信号的最优轨迹完全在移动时间窗口内描述,但实际的控制输入只取控制信号的第一个样本,而忽略了轨迹的其余部分。
- 当前状态:在规划过程中,需要时刻的信息来预测未来。这个信息描述为
,这是包含了相关因素的向量,通常是测量或预测得到的。
- 模型:在预测控制中,描述系统动态的模型至关重要。一个好的动态模型能对未来做出准确一致的预测。
- 代价函数:为了做出最优决策,需要一个标准来衡量达到期望目标的程度。用来反映期望目标与实际响应之间差别的函数叫做目标函数,通常也叫做代价函数J,在优化窗口内使代价函数最小的控制轨迹,就是最优规划轨迹。
1.2 预测控制中的模型
模型的表示方式有几种:FIR(有限冲击响应)模型、阶跃响应模型、传递函数模型、状态空间模型等。不同的模型表示方式,对应的预测控制算法不一样。基于FIR或阶跃响应模型的控制算法包括动态矩阵控制(DMC)以及二次型DMC。但是这种方法仅限于稳定的控制对象,而且需要非常大的模型阶数和非常多的模型系数。传递函数模型能更简洁的描述过程动力学,适用于稳定和不稳定对象。基于传递函数的控制算法代表包括Peterka的预测控制算法和Clarke等人的广义预测控制算法。但是传递函数模型在处理多变量对象时效率较低。状态空间模型用于预测控制设计越来越多。本文也将使用状态空间模型。
二、从连续时间模型到增广模型
2.1 连续模型到离散模型
连续时间状态空间模型可以表示为:
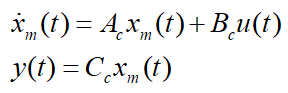
对应的离散时间状态空间模型可以表示为:

在MATLAB中可以通过c2dm函数,并指定一个采样时间间隔Δt,将连续模型转换成离散模型。
例:给定连续时间状态空间模型如下,求出对应的离散时间状态空间模型,采样时间间隔为1。
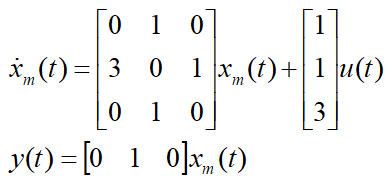
MATLAB程序如下:
Ac = [0 1 0; 3 0 1; 0 1 0 ];
Bc= [1; 1; 3];
Cc=[0 1 0];
Dc=zeros(1,1);
Delta_t=1;
[Ad,Bd,Cd,Dd]=c2dm(Ac,Bc,Cc,Dc,Delta_t);得到的离散模型矩阵如下:

2.2 离散模型到增广模型
增广模型如下:
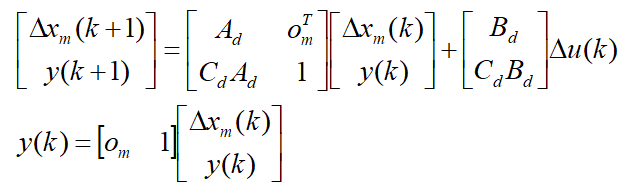
其中,
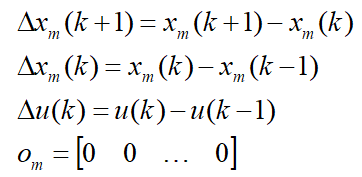
增广模型的矩阵分别为:
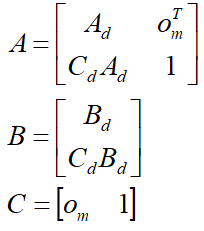
例:离散时间状态空间模型的系统矩阵如下,求对应的增广模型矩阵(A,B,C)。
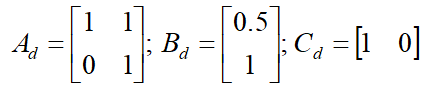
首先要确定的列数,由增广模型可知,
的列数与
的行数相同,那么
, 将
代入增广模型矩阵方程中,就可以得到增广模型矩阵:
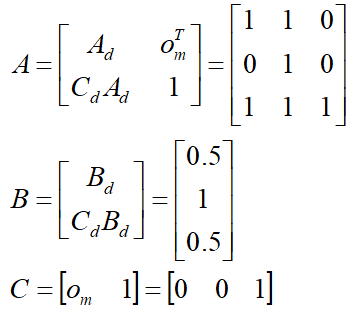
用MATLAB实现上述过程如下:
Ad = [1 1;0 1];
Bd = [0.5;1];
Cd = [1 0];[m1,n1]=size(Cd);
[n1,n_in]=size(Bd);
A_e=eye(n1+m1,n1+m1);
A_e(1:n1,1:n1)=Ad;
A_e(n1+1:n1+m1,1:n1)=Cd*Ad;
B_e=zeros(n1+m1,n_in);
B_e(1:n1,:)=Bd;
B_e(n1+1:n1+m1,:)=Cd*Bd;
C_e=zeros(m1,n1+m1);
C_e(:,n1+1:n1+m1)=eye(m1,m1);得到的结果如下:
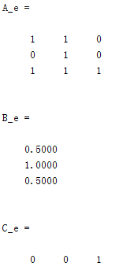
与直接代入计算的结果完全相同,验证了MATLAB程序的正确性。
三、状态预测与优化
3.1 状态和输出变量的预测
假设当前时刻为,
为通过检测得到的系统状态变量,这里假设状态变量可以检测到。那么
个未来的控制变量序列表示为:
![]()
(不是表示当前的时刻吗,为什么
又表示的未来的控制量?因为当前时刻的控制量也需要通过优化才能得出,所以相对来说
也是未来的控制量)
个预测的状态变量表示为:
![]()
代入增广模型中,得到个预测的状态变量为:
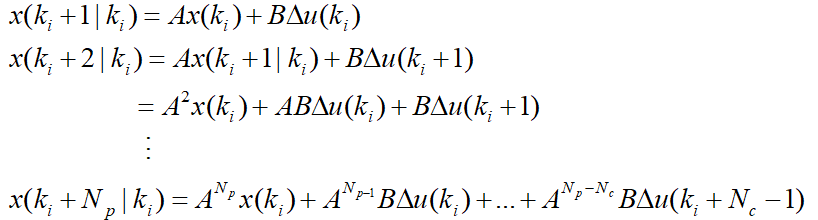
那么,个预测的输出变量为:
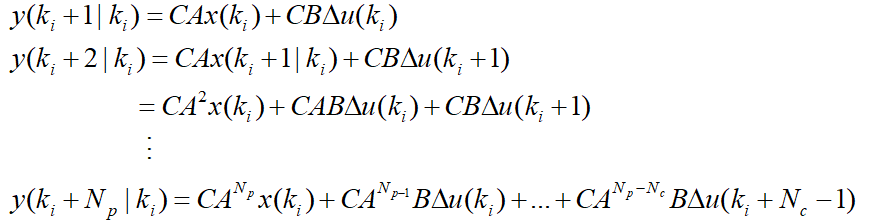
可以看出,所有预测的变量都只与当前观测到的系统状态以及未来的控制变量序列有关:
![]()
将未来的输出变量序列和未来的控制变量序列写成:
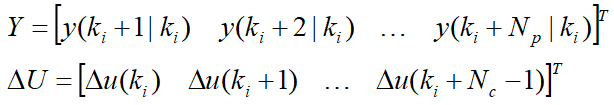
在单输入,单输出系统中,Y的维数是,
的维数是
。将上式合起来写得到:
![]()
其中,
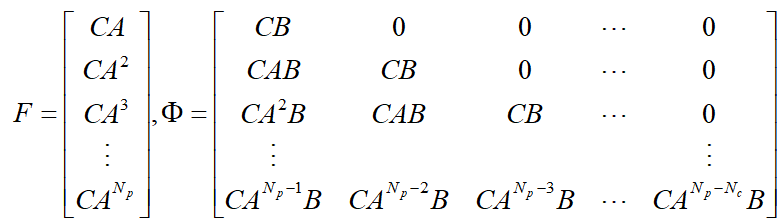
3.2 优化
在时刻的期望输入值为
,需要通过MPC控制,让系统输出尽可能的接近系统输入。假设在优化窗口内,输入是恒定值。问题就转化成了需要在优化窗口内,找到一个最佳的控制变量序列,使得系统输出与输入的误差最小。
将输入改写成优化窗口内的输入序列:
![]()
序列长度为,定义代价函数为:
![]()
代价函数的第一项反映了输入信号与预测的输出信号之间的误差,第二项则是为了限制控制量,避免控制量太大。其中
是对角矩阵:
![]()
其中,是影响闭环性能的可调参数。如果
,则说明不用考虑控制变量
有多大,只考虑控制误差越小越好。如果
取值比较大,则表示需要仔细考虑
的大小。
将代价函数写成:
![]()
要求上述代价函数的最小值,最简单粗暴的方法就是求一阶导:
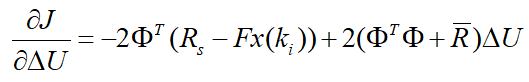
当一阶导为零时,可以求得控制变量的最优解:
![]()
其中,假设了矩阵存在。将优化的
写成与
和
有关的形式为:
![]()
其中,长度为
。至此,就将优化的控制序列求解出来了。
例:一阶系统状态空间方程如下:
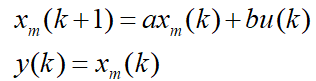
其中,,求(1)增广状态空间模型;(2)计算矩阵
;(3)假设在时刻
,
,当
分别为0和10的时候,求解最优
,并比较结果。
解:增广状态空间方程为:
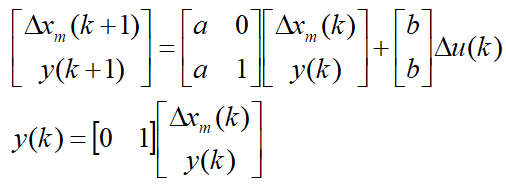
矩阵如下:
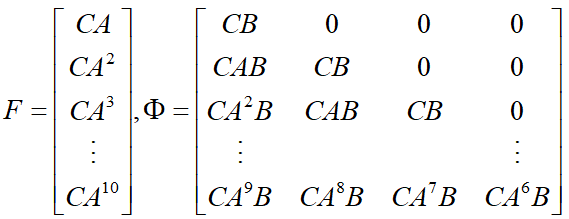
矩阵中的系数计算方式如下:
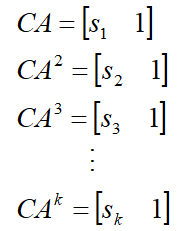
其中,
![]()
矩阵中的系数计算方式如下:
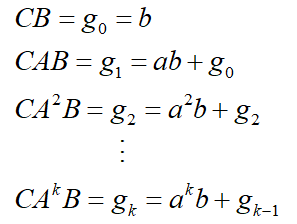
将代入得到:

当时,即控制系统只考虑减小输入输出的误差,不考虑控制量大小的情况下,计算得到的
个控制量序列为:
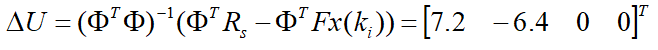
可以看出控制量变化比较大。
当时,即限制了控制量变化大小的情况下,计算得到的
个控制量序列为:
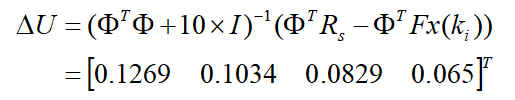
与之前一种情况相比,控制量平稳很多。
将这两种情况下的输出量和状态量曲线画出来如下图所示。可以看到时状态变化量减少到0时,预测输出可以到达期望输入。而在
时,预测输出缓慢向期望输入靠近,在预测窗口内误差比较大,收敛速度比
慢,但是状态变化曲线更加平稳。
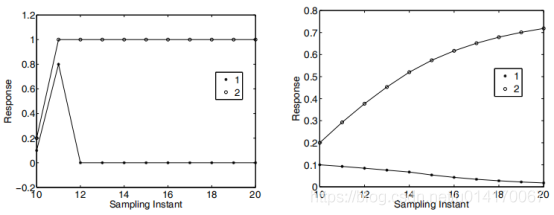
图1 和
时状态变化及输出量曲线
由上述对比可以看出,如果想要控制量更平稳的变化,那么控制信号达到稳定状态需要更长的时间。如果将控制域从增加到
,在
的时候得到的最优控制量序列为:
![]()
可以看出,前四个数值都不一样,而且都有所减少。在不同情况下,要根据实际需要选择合适的来进行MPC控制。
3.3 MATLAB实现
用MATLAB函数实现上述计算各矩阵的过程,最关键的是求矩阵。其中
是托普利兹矩阵,通过定义其第一列,后面的列都可以通过移动前一列获得。
定义一个函数,函数的输入是离散时间状态空间模型以及预测时域和控制时域长度
。MATLAB程序如下:
function [Phi_Phi,Phi_F,Phi_R,A_e, B_e,C_e]=mpcgain(Ap,Bp,Cp,Nc,Np)
[m1,n1]=size(Cp);
[n1,n_in]=size(Bp);
A_e=eye(n1+m1,n1+m1);
A_e(1:n1,1:n1)=Ap;
A_e(n1+1:n1+m1,1:n1)=Cp*Ap;
B_e=zeros(n1+m1,n_in);
B_e(1:n1,:)=Bp;
B_e(n1+1:n1+m1,:)=Cp*Bp;
C_e=zeros(m1,n1+m1);
C_e(:,n1+1:n1+m1)=eye(m1,m1);n=n1+m1;
h(1,:)=C_e;
F(1,:)=C_e*A_e;
for kk=2:Np
h(kk,:)=h(kk-1,:)*A_e;
F(kk,:)= F(kk-1,:)*A_e;
end
v=h*B_e;
Phi=zeros(Np,Nc); %declare the dimension of Phi
Phi(:,1)=v; % first column of Phi
for i=2:Nc
Phi(:,i)=[zeros(i-1,1);v(1:Np-i+1,1)]; %Toeplitz matrix
end
BarRs=ones(Np,1);
Phi_Phi= Phi'*Phi;
Phi_F= Phi'*F;
Phi_R=Phi'*BarRs;为了验证程序的正确性,在MATLAB的work space输入:
Ap = 0.8;
Bp = 0.1;
Cp = 1;
Nc = 4;
Np = 10;
[Phi_Phi, Phi_F, Phi_R, A_e, B_e, C_e] = mpcgain(Ap, Bp, Cp, Nc, Np);运行后得到:
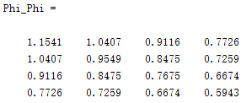


可以看出计算结果与上例中的相同,表明程序正确。
四、参考文献
[1] Liuping Wang. Model Predictive Control System Design and Implementation Using MATLAB.