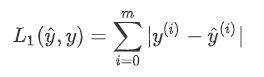一、自动控制原理 ¹

1. 控制原理

1.1 开环与闭环系统

下面是开环系统与闭环系统的示例。以给水壶加热的过程举例，开环系统只是简单的利用开关信号控制水壶的加热。而下图的闭环控制系统中，将添加温度传感器所测量的信号作为系统的反馈量。设计控制系统的核心就是通过对闭环系统的控制器进行调整，利用反馈量信号，完成闭环的稳定控制。

同时，这就是反馈的过程。

简单的开环系统有如下描述：（这里以流体力学的公式作为举例）

添加控制器D(s)，并增加测量H(s)，构成如下闭环系统。但是在分析闭环系统的稳定性时，一般的做法是将其转换成为开环系统，并将新构造的开环系统传递函数作为研究对象，分析系统的稳定性。

1.2 稳定性分析²

1.3 一起燃烧卡路里/科学减肥（系统分析实例_数学建模部分）

框图表示如下：

设计比例控制器（最为简单的控制器）如下：
$$u=k_{p}e$$
那么如何设计该控制器，让最终的系统趋向于稳定状态呢？（也就是说传递函数的极点在左半边平面）

学习控制理论一定要从微分方程入手，弄清楚微分方程与传递函数之间的关系就会容易理解很多。

通过对于比例控制器的分析之后发现，单纯的比例控制最终产生稳态误差。

1.4 终值定理与稳态误差³

1）比例控制

举例说明。下面是一个最为简单的一阶系统，采用的控制方式是比例控制。

利用定理分析稳态误差如下：

这里说明了比例控制的局限性，必须采用更加实用性的控制算法。比例控制充法消除稳态误差

2）比例积分控制

并有下面变换方式：

通过引入一个积分信号，让本来的一阶系统变成一个二阶系统。

1.5 根轨迹

再回到弹簧系统，是一个二阶系统。

对于高阶系统不过也是几个一阶系统的叠加，如下：

这一节评估了根的位置对于控制器的影响。

1.6 PID控制

• 比例控制
• 微分控制：调节水温变化的速度，
• 积分控制：误差的累计量

注意：

• 比例积分控制没有单独的比例控制收敛快
• 微分控制解决了超调量问题
• 微分控制的问题是初始状态下的输入值很大
• 同时，微分控制的控制量受到测量误差的影响非常大。他对噪声非常敏感

示例：

在无人机中，利用串联PID控制完成姿态和高度控制是比较经典的方法，参考博客。

如果想增加飞行器的稳定性(增加阻尼)并提高它的控制品质，我们可以进一步的控制它的角速度，于是角度/角速度-串级PID控制算法应运而生。在这里，相信大多数朋友已经初步了解了角度单环PID的原理，但是依旧无法理解串级PID究竟有什么不同。其实很简单：它就是两个PID控制算法，只不过把他们串起来了(更精确的说是套起来)。那这么做有什么用？答案是，它增强了系统的抗干扰性(也就是增强稳定性)，因为有两个控制器控制飞行器，它会比单个控制器控制更多的变量，使得飞行器的适应能力更强。为了更为清晰的讲解串级PID，这里笔者依旧画出串级PID的原理框图。

2. 数学工具

2.2 拉普拉斯逆变换⁴

2.3 矩阵的性质[^5]

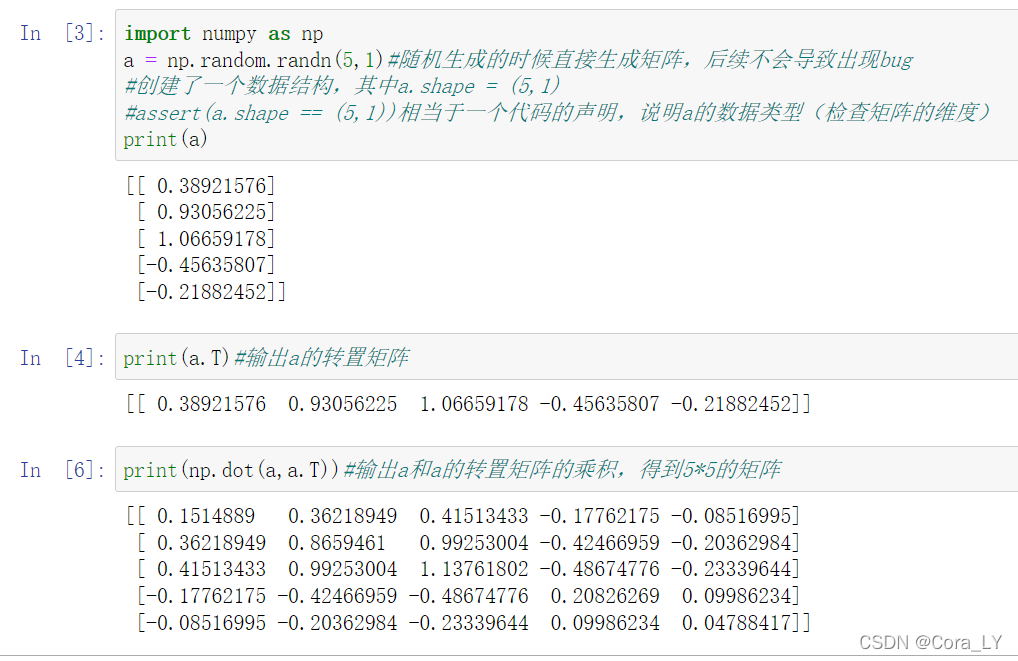
矩阵有下面的性质，现代控制理论的分析中常常会用到。

2.4 bode图

给信号滤波的过程中，需要注意幅频响应。如果在带通范围内不是1的话，就会改变信号的幅值，就会改变最终加速度输出的信号。另外，上面的图就是bode图，但是是基于离散系统的。

1. 如何去理解bode图？

%% 这个是正解
b = [1,2,3];
a = [2,1,3];
figure;bode(b,a)
% 
[h1 , ftp] = freqs(b,a);
mag = 20*log10(abs(h1));    % get magnitude of spectrum in dB
phase = angle(h1)/pi*180;     % get phase in deg.
figure
semilogx(ftp,mag)
xlabel('Frequency (Hz)'),ylabel('Magnitude (dB)')

2. 从一个实例出发理解bode图

对于系统传递函数：
$$G(s)=\frac{a}{s+a}$$
分析频率响应：
$$|G(j\omega )|=\sqrt{\frac{1}{1+{\left(\frac{\omega }{a}\right)}^2}}$$

$$\angle G(j\omega )=-\arctan \left(\frac{w}{a}\right)$$

• 低频：w<<a

$$\begin{array}{l}|G(j\omega )|=1\\ 20\log |G(j\omega )|=0\\ \angle G(j\omega )=0\end{array}$$

• 截止频率：w=a

这个-3dB很重要，表达的是输出的振幅是输入的振幅的sqrt(1/2)，能量是一半的关系。

$$\angle G(gw)=-\arctan 1=-45^{\circ }$$

• 高频：w>>a

bode图如下：

3. bode图的作用是什么？

实际上，我们可以将级联系统的子系统bode图进行累加，那么我们就得到了新的级联系统的真正的bode图了。原理如上。

2.5 单位冲激函数

二、 现代控制原理串讲

1. 现代控制理论概要

首先要了解一个简单的弹簧阻尼模型，作为控制的对象，其满足胡克定律。
$$\begin{array}{l}\dot{x}=kx\\ \ddot{x}=Bx\end{array}$$
描述现代控制理论中的系统，最基础的当然是状态空间表示法：

当然，通过拉普拉斯变换可以转换成下面的形式，控制对象是弹簧阻尼块。

其中有一条重要的信息，实际上矩阵A的特征值就是G(s)的极点，决定了系统的稳定性。上面的右式时通用的。

去分析一个系统，主要需要考虑以下几个重要的性质。

（那么对于自动控制，只需要极点就够了）

• 可控性

  

• 李雅普诺夫稳定性：确定系统的稳定状态，控制系统可以满足数学的条件。在一阶系统中，常常用极点分析的方法去观察稳定性。现代控制理论中常用到的分析系统的方法就是去找系统的V函数，得到最后是不是能够

• 可观性：状态观测器。系统状态加入不可直接测量，那么就需要通过输出和控制量去估计状态。状态观测器需要达到一个收敛的状态。建立观测器时，实际上是建立一个反馈系统，使得误差等于0。（这里是不是有误差状态量的部分？）

  对于可观测性，需要问一个问题：是不是所有系统都是可测的？借鉴可控性的推导，有下面的结论：

  

2. 怎样去分析一个状态空间方程系统呢？

实际上看到设计控制器就是去配置特征值的过程。这里的特征值有点像自动控制原理中的极点的概念，决定了系统随时间是收敛的，还是振动的，还是逼近于无穷的。

下面是对于一个控制系统的分析过程，利用配置特征值的方法可以确定比例控制的控制系数u与状态量x之间的关系。

三、最后的一些思考

轨迹跟踪与制导之间的关系

轨迹跟踪的目标是使状态和参考状态的误差保持在0附近。举例，对深空飞行器而言，按照轨迹优化+轨迹跟踪这两个步骤实现控制。参考轨迹是人为设计的，可以是全局最优的，也可以是次优的。然后把跟踪误差保持在0附近，这也有一套控制律，比如LQR轨迹跟踪器。

状态控制按照给定的控制律，在航天器轨迹控制中叫做制导；在姿态控制中好像没见过先设计好姿态运动规律的，都是即时控制。制导律必须全局渐进稳定，适用于高动态的环境，比如空空导弹采用比例导引法。