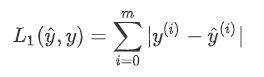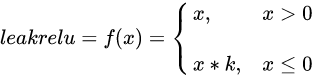#吴恩达《深度学习》L1W2作业1 知识点:numpy入门,函数向量化实现
'''
做完这个作业,你能学会:用ipython notebook
用numpy,包括函数调用及向量矩阵运算
理解“广播”的概念
向量化代码
'''
#我们很少在深度学习中使用“math”库。 因为math函数的输入是实数.
#而深度学习中主要使用的是矩阵和向量,因此numpy更为实用。
a=5
b=[1,2,3,4]
import math
math.exp(a)![]()
math.exp(b)
import numpy as np
np.exp(a)![]()
np.exp(b)![]()
#np.exp? (例如)快速访问使用文档。
np.exp? 
#定义两个函数,分别是sigmoid函数和sigmoid_derivative函数;
#sigmoid函数是逻辑函数;sigmoid_derivative是逻辑回归的求导函数;
#sigmoid(x)=1/(1+exp(-x))
#sigmoid_derivative(x)=sigmoid(x)*(1-sigmoid(x))def sigmoid(x):return 1/(1+np.exp(x))def sigmoid_derivative(x):return sigmoid(x)*(1-sigmoid(x))
#对实数适用;
sigmoid(a),sigmoid_derivative(a)
#重塑数组,深度学习中两个常用的numpy函数是np.shape和np.reshape()。
'''
例如,在计算机科学中,图像由shape为(length,height,depth=3)的3D数组表示。但是,当你读取图像作为算法的输入时,
会将其转换为维度为(length*height*depth,1)的向量。换句话说,将3D阵列“展开”或重塑为1D向量。
'''
#定义图像转向量的方法;也可以定义向量转图像的方法;def image_to_vector(input_image):output_vector=np.reshape(input_image,(-1,1))return output_vectordef vector_to_image(input_vector,length,height,depth):out_image=np.reshape(input_vector,(length,height,depth))return out_image#图像示例
image = np.array([[[ 0.67826139, 0.29380381],[ 0.90714982, 0.52835647],[ 0.4215251 , 0.45017551]],[[ 0.92814219, 0.96677647],[ 0.85304703, 0.52351845],[ 0.19981397, 0.27417313]],[[ 0.60659855, 0.00533165],[ 0.10820313, 0.49978937],[ 0.34144279, 0.94630077]]])import matplotlib.pyplot as plt image.shape ![]()
#图像转向量
vector1=image_to_vector(image)
#向量转图像
image1=vector_to_image(vector1,3,3,2)vector1.shape,image1.shape ![]()
#对行执行标准化
'''
我们在机器学习和深度学习中使用的另一种常见技术是对数据进行标准化。 由于归一化后梯度下降的收敛速度更快,通常会表现出更好的效果。
通过归一化,也就是将x更改为x/norm(x)(将x的每个行向量除以各行的范数)。x是数组或者类数组。
'''
#定义normalizeRowsdef normalizeRows(x):rows_norm=np.linalg.norm(x,axis=1).reshape(-1,1)x_norm=x/rows_normreturn x_norm
x = np.array([[0, 3, 4],[1, 6, 4]])normalizeRows(x) 
#axis=1对行运算;axis=0对列运算
np.linalg.norm(x,axis=1),np.linalg.norm(x,axis=0) ![]()
# 广播和softmax函数
'''
在numpy中要理解的一个非常重要的概念是“广播”。
这对于在不同形状的数组之间执行数学运算非常有用。
使用numpy实现softmax函数。
你可以将softmax理解为算法需要对两个或多个类进行分类时使用的标准化函数。总结一下softmax如何将多分类输出转换为概率,可以分为两步:1)分子:通过指数函数,将实数输出映射到零到正无穷。2)分母:每行将所有结果相加。
这样得到的数组,每行之和都是1.
'''
def softmax(x):exp_x=np.exp(x)sum_exp_x=np.sum(exp_x,axis=1).reshape(-1,1)softmax_x=exp_x/sum_exp_xreturn softmax_xx = np.array([[9, 2, 5, 0, 0],[7, 5, 0, 0 ,0]])softmax(x),np.sum(softmax(x),axis=1) 
#向量化
'''
在深度学习中,通常需要处理非常大的数据集。 因此,
非计算最佳函数可能会成为算法中的巨大瓶颈,并可能使模型运行一段时间。
为了确保代码的高效计算,我们将使用向量化。
例如,尝试区分点/外部/元素乘积之间的区别。
'''
'''
向量化的实现更加简洁高效。 对于更大的向量/矩阵,运行时间的差异变得更大。
不同于np.multiply()和* 操作符(相当于Matlab / Octave中的 .*)执行逐元素的乘法,
np.dot()执行的是矩阵-矩阵或矩阵向量乘法,
'''
b=[1,2,3,4]b1=np.array(b).reshape(1,4)
b2=b1.reshape(4,1)
b1,b2 

#实现L1和L2损失函数
'''
损失函数用于评估模型的性能。 损失越大,预测() 与真实值()的差异也就越大。 在深度学习中,
我们使用诸如Gradient Descent之类的优化算法来训练模型并最大程度地降低成本。'''
'''
h:预测值;y,实际值。L1=sum(abs(h-y))L2=sum((h-y)**2)a**2,为a的2次方。
'''def L1(h,y):return sum(np.abs(h-y))def L2(h,y):return sum((h-y)**2)h= np.array([.9, 0.2, 0.1, .4, .9])
y = np.array([1, 0, 0, 1, 1])
L1(h,y),L2(h,y) ![]()
'''
你需要记住的内容:
-向量化在深度学习中非常重要, 它保证了计算的效率和清晰度。
-了解L1和L2损失函数。
-掌握诸多numpy函数,例如np.sum,np.dot,np.multiply,np.maximum等。
'''https://www.heywhale.com/mw/project/5dd236a800b0b900365eca9b