本文主要参考了 严宽 大神的学习笔记,并在其基础上补充了一点内容,点此查看原文。
本文所使用的资料已上传到百度网盘【点击下载】,提取码:hnwl ,请在开始之前下载好所需资料。
到目前为止,哦我们始终都是在使用梯度下降法学习,本文中,我们将使用一些更加高级的优化算法,利用这些优化算法,通常可以提高我们算法的收敛速度,并在最终得到更好的分离结果。这些方法可以加快学习速度,甚至可以为成本函数提供更好的最终值,在相同的结果下,有一个好的优化算法可以减少几个小时甚至几天的时间。
我们想象一下成本函数 J J J,最小化成本就像找到丘陵的最低点,在训练的每一步中,都会按照某个方向更新参数,以尽可能达到最低点。它类似于最快的下山的路,如下图:
import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasetsimport opt_utils #参见数据包
import testCase #参见数据包#%matplotlib inline #如果你用的是Jupyter Notebook请取消注释
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
一、优化算法
1. 梯度下降
在机器学习中,最简单的就是没有任何优化的梯度下降(GD,Gradient Descent),我们每一次循环都是对整个训练集进行学习,这叫做批量梯度下降(Batch Gradient Descent),我们之前说过了最核心的参数更新的公式,即: W [ l ] = W [ l ] − α d W [ l ] W^{[l]}=W^{[l]}-\alpha\ dW^{[l]} W[l]=W[l]−α dW[l] b [ l ] = b [ l ] − α d b [ l ] b^{[l]}=b^{[l]}-\alpha\ db^{[l]} b[l]=b[l]−α db[l] 下面我们实现梯度下降算法更新参数:
def update_parameters_with_gd(parameters, grads, learning_rate):"""使用梯度下降更新参数参数:parameters - 字典,包含了要更新的参数:parameters['W' + str(l)] = Wlparameters['b' + str(l)] = blgrads - 字典,包含了每一个梯度值用以更新参数grads['dW' + str(l)] = dWlgrads['db' + str(l)] = dbllearning_rate - 学习率返回值:parameters - 字典,包含了更新后的参数"""L = len(parameters) // 2 # 更新每个参数for l in range(L):parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]return parameters
测试:
#测试update_parameters_with_gd
print("-------------测试update_parameters_with_gd-------------")
parameters , grads , learning_rate = testCase.update_parameters_with_gd_test_case()
parameters = update_parameters_with_gd(parameters,grads,learning_rate)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
测试结果如下:
W1 = [[ 1.63535156 -0.62320365 -0.53718766][-1.07799357 0.85639907 -2.29470142]]
b1 = [[ 1.74604067][-0.75184921]]
W2 = [[ 0.32171798 -0.25467393 1.46902454][-2.05617317 -0.31554548 -0.3756023 ][ 1.1404819 -1.09976462 -0.1612551 ]]
b2 = [[-0.88020257][ 0.02561572][ 0.57539477]]
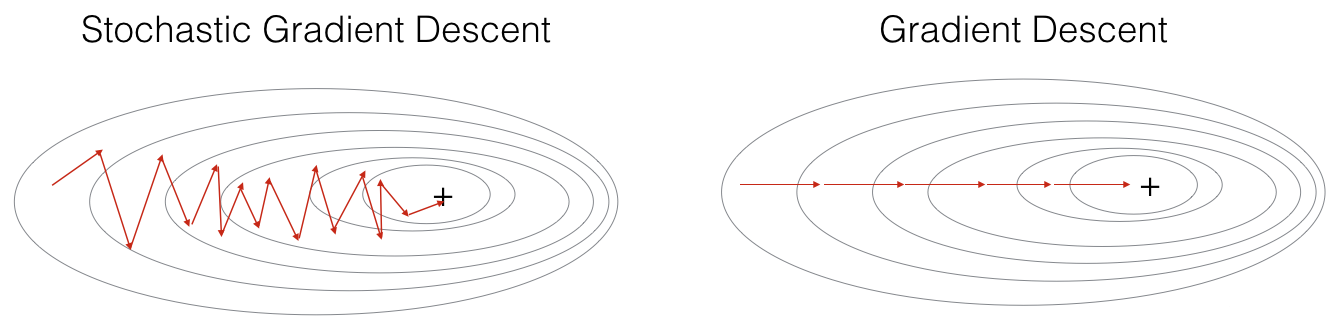
由梯度下降算法演变来的还有 随机梯度下降(SGD) 和 小批量梯度下降(mini-batch)。
在随机梯度下降算法中,每次迭代中仅使用其中一个样本,当训练集很大时,使用随机梯度下降算法的运行速度会很快,但是会存在一定的波动。
#随机梯度下降算法:
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in (0,num_iterations):for j in m:#前向传播A,cache = forward_propagation(X,parameters)#计算成本cost = compute_cost(A,Y)#后向传播grads = backward_propagation(X,Y,cache)#更新参数parameters = update_parameters(parameters,grads)
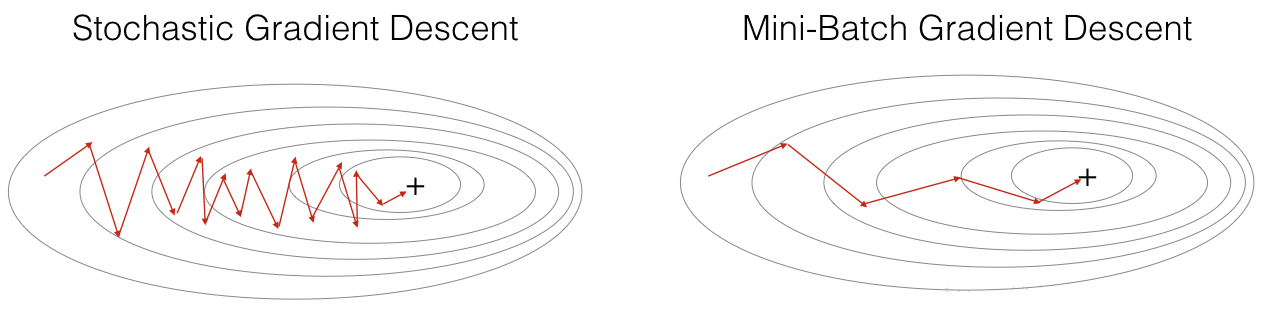
小批量梯度下降法实际是综合了梯度下降法和随机梯度下降法的方法,在它的每次迭代中,既不是选择全部的数据来学习,也不是选择一个样本来学习,而是把所有的数据集分割为一小块一小块的来学习,它会随机选择一小块,块大小一般为 2 n 2^n 2n。这样做的好处是:一方面可以充分利用 GPU 的并行性,另一方面不会让计算时间特别长。
2. mini-batch 梯度下降法
使用 mini-batch 梯度下降法要经过以下两个步骤:
-
把训练集随机打乱,但是 X X X 和 Y Y Y 依旧是一一对应的,即:打乱后 X X X 的第 i i i 列与 Y Y Y 中的第 i i i 个标签仍然是对应的。这里 X X X 和 Y Y Y 的每一列代表一个样本。
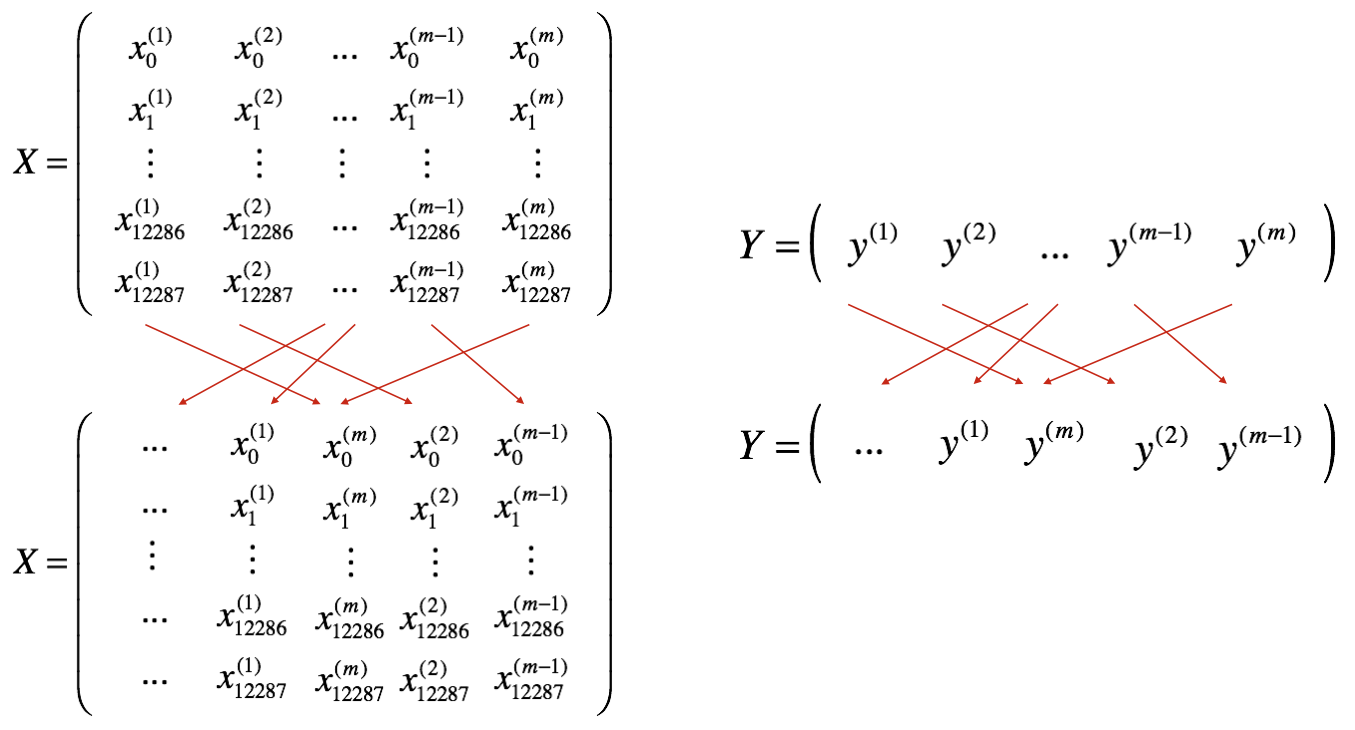
-
切分。我们把训练集大乱之后,将其切分为若干份。这里切分的大小是 64
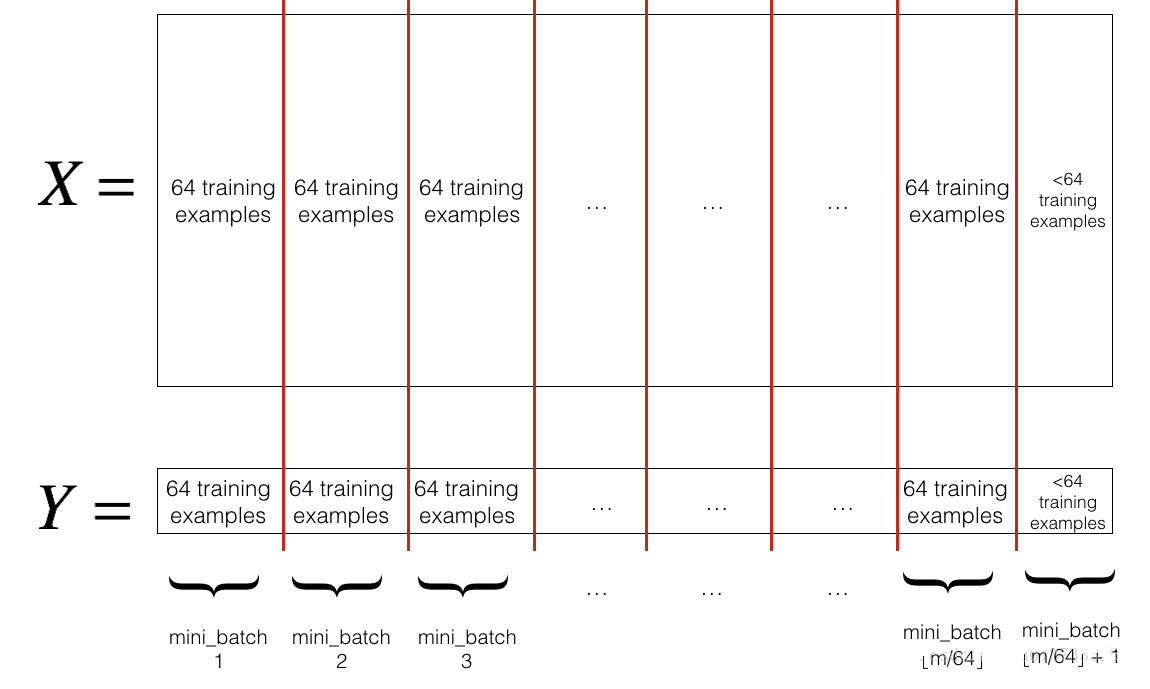
我们先来看看分割后如何获取第一第二个 mini-batch 吧
# 第一个mini-batch
first_mini_batch_X = shuffled_X[:, 0 : mini_batch_size]
# 第二个mini-batch
second_mini_batch_X = shuffled_X[:, mini_batch_size : 2 * mini_batch_size]
我们先来看看 np.random.permutation(m) 的用法:
x = np.array([[1,2,3,4,5,6,7,8,9],[9,8,7,6,5,4,3,2,1]])
y = np.array([[1,0,1,0,1,0,1,0,1]])permutation=list(np.random.permutation(9))
shuffled_X = X[:,permutation]
shuffled_Y = Y[:,permutation].reshape((1,m))
print(permutation)
print(shuffled_X )
print(shuffled_Y )
运行结果如下:
[6, 0, 5, 7, 4, 3, 1, 8, 2]
[[7 1 6 8 5 4 2 9 3][3 9 4 2 5 6 8 1 7]]
[[1 1 0 0 1 0 0 1 1]]
下面就是我们获取 mini-batch 的代码:
def random_mini_batches(X, Y, mini_batch_size=64, seed=0):"""从(X,Y)中创建一个随机的mini-batch列表参数:X - 输入数据,维度为(输入节点数量,样本的数量)Y - 对应的是X的标签,【1 | 0】(蓝|红),维度为(1,样本的数量)mini_batch_size - 每个mini-batch的样本数量返回:mini-bacthes - 一个同步列表,维度为(mini_batch_X,mini_batch_Y)"""np.random.seed(seed)m = X.shape[1]mini_batches = []# 第一步:打乱顺序## 它会返回一个长度为 m 的随机数组,且里面的数是 0 到 m-1permutation = list(np.random.permutation(m))## 将每一列的数据按 permutation 的顺序来重新排列shuffled_X = X[:, permutation]shuffled_Y = Y[:, permutation].reshape((1, m))# 第二步:分割## 把你的训练集分割成多少份,请注意,如果值是99.99,那么返回值是99,剩下的0.99会被舍弃num_complete_minibatches = math.floor(m / mini_batch_size)for k in range(0, num_complete_minibatches):mini_batch_X = shuffled_X[:, k * mini_batch_size : (k+1) * mini_batch_size]mini_batch_Y = shuffled_Y[:, k * mini_batch_size : (k+1) * mini_batch_size]mini_batch = (mini_batch_X, mini_batch_Y)mini_batches.append(mini_batch)# 如果训练集的大小刚好是 mini_batch_size 的整数倍,那么这里已经处理完了# 如果训练集的大小不是 mini_batch_size 的整数倍,那么最后肯定会剩下一些,我们要把它处理了if m % mini_batch_size != 0:# 获取最后剩余的部分mini_batch_X = shuffled_X[:, mini_batch_size * num_complete_minibatches:]mini_batch_Y = shuffled_Y[:, mini_batch_size * num_complete_minibatches:]mini_batch = (mini_batch_X, mini_batch_Y)mini_batches.append(mini_batch)return mini_batches
测试:
#测试random_mini_batches
print("-------------测试random_mini_batches-------------")
X_assess,Y_assess,mini_batch_size = testCase.random_mini_batches_test_case()
mini_batches = random_mini_batches(X_assess,Y_assess,mini_batch_size)print("第1个mini_batch_X 的维度为:",mini_batches[0][0].shape)
print("第1个mini_batch_Y 的维度为:",mini_batches[0][1].shape)
print("第2个mini_batch_X 的维度为:",mini_batches[1][0].shape)
print("第2个mini_batch_Y 的维度为:",mini_batches[1][1].shape)
print("第3个mini_batch_X 的维度为:",mini_batches[2][0].shape)
print("第3个mini_batch_Y 的维度为:",mini_batches[2][1].shape)
测试结果如下:
-------------测试random_mini_batches-------------
第1个mini_batch_X 的维度为: (12288, 64)
第1个mini_batch_Y 的维度为: (1, 64)
第2个mini_batch_X 的维度为: (12288, 64)
第2个mini_batch_Y 的维度为: (1, 64)
第3个mini_batch_X 的维度为: (12288, 20)
第3个mini_batch_Y 的维度为: (1, 20)
3. 包含动量的梯度下降(momentum)
由于小批量梯度下降只看到了一个子集的参数更新,更新的方向有一定的差异,所以小批量梯度下降的路径将“振荡地”走向收敛,尤其对于W、b之间数值范围差别较大的情况。此时每一点处的梯度只与当前方向有关,产生类似折线的效果,前进缓慢。而如果对梯度进行指数加权平均,这样使当前梯度不仅与当前方向有关,还与之前的方向有关,这样处理让梯度前进方向更加平滑,减少振荡,能够更快地到达最小值处。我们把以前梯度的方向存储在变量 v 中,从形式上讲,这将是前面的梯度的 指数加权平均值。我们也可以把 v 看作是滚下坡的速度,根据山坡的坡度建立动量。如图所示:
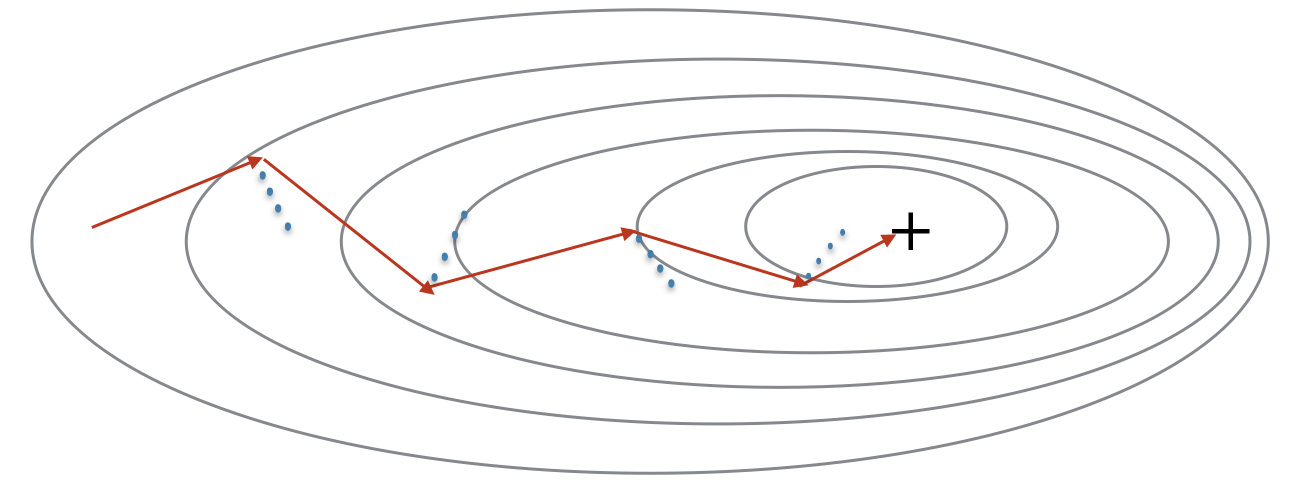
其中,红色箭头显示具有动量的小批量梯度下降一步时所采取的方向,蓝色的点显示每个步骤的梯度方向(相对于当前的小批量)。当然我们不仅要观察梯度,还要让 v v v 影响梯度的方向,尽量让前进的方向指向最小值。既然我们要影响梯度的方向,而梯度需要使用到 dW 和 db,那么我们就要建立一个和 dW 和 db 相同结构的变量来影响他们,我们现在来进行初始化:
def initialize_velocity(parameters):"""初始化速度,velocity是一个字典:- keys: "dW1", "db1", ..., "dWL", "dbL" - values:与相应的梯度/参数维度相同的值为零的矩阵。参数:parameters - 一个字典,包含了以下参数:parameters["W" + str(l)] = Wlparameters["b" + str(l)] = bl返回:v - 一个字典变量,包含了以下参数:v["dW" + str(l)] = dWl的速度v["db" + str(l)] = dbl的速度"""L = len(parameters) // 2 #神经网络的层数v = {}for l in range(L):v["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])v["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])return v
测试:
#测试initialize_velocity
print("-------------测试initialize_velocity-------------")
parameters = testCase.initialize_velocity_test_case()
v = initialize_velocity(parameters)print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))
测试结果如下:
-------------测试initialize_velocity-------------
v["dW1"] = [[0. 0. 0.][0. 0. 0.]]
v["db1"] = [[0.][0.]]
v["dW2"] = [[0. 0. 0.][0. 0. 0.][0. 0. 0.]]
v["db2"] = [[0.][0.][0.]]
权重 W 和常数项 b 的指数加权平均表达式如下: V d W = β ⋅ V d W + ( 1 − β ) ⋅ d W V_{dW}=\beta·V_{dW}+(1-\beta)·dW VdW=β⋅VdW+(1−β)⋅dW V d b = β ⋅ V d b + ( 1 − β ) ⋅ d b V_{db}=\beta·V_{db}+(1-\beta)·db Vdb=β⋅Vdb+(1−β)⋅db 从动量的角度来看,以权重 W 为例, V d W V_{dW} VdW 可以看成速度 v, d W dW dW 可以看成是速度 a。指数加权平均实际上是计算当前的速度,当前速度由之前的速度和现在的加速度共同影响。而 β < 1 \beta < 1 β<1,又能限制 V d W V_{dW} VdW 过大。也就是说,当前的速度是渐变的,而不是瞬变的,是动量的过程。这保证了梯度下降的平稳性和准确性,减少振荡,较快地达到最小值处。
动量梯度下降算法的过程如下:
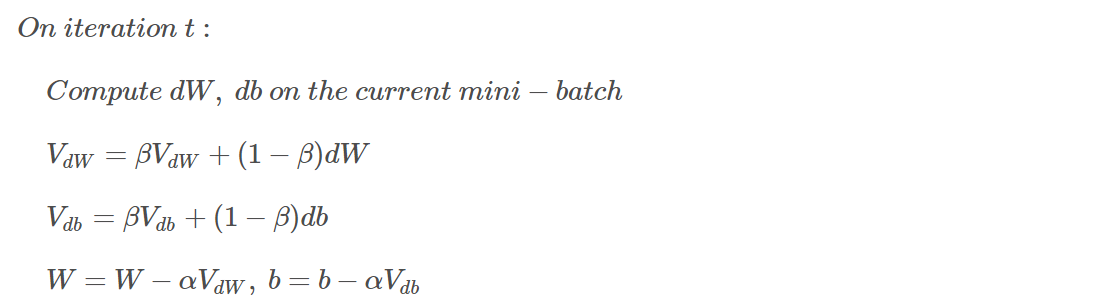
初始时,令 V d W = 0 V_{dW}=0 VdW=0, V d b = 0 V_{db}=0 Vdb=0。一般设置 β = 0.9 \beta=0.9 β=0.9,即指数加权平均前 10 天的数据,实际应用效果较好。
def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):"""使用动量更新参数参数:parameters - 一个字典类型的变量,包含了以下字段:parameters["W" + str(l)] = Wlparameters["b" + str(l)] = blgrads - 一个包含梯度值的字典变量,具有以下字段:grads["dW" + str(l)] = dWlgrads["db" + str(l)] = dblv - 包含当前速度的字典变量,具有以下字段:v["dW" + str(l)] = ...v["db" + str(l)] = ...beta - 超参数,动量,实数learning_rate - 学习率,实数返回:parameters - 更新后的参数字典v - 包含了更新后的速度变量"""L = len(parameters) // 2for l in range(L):# 计算速度v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] + (1 - beta) * grads["dW" + str(l + 1)]v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * grads["db" + str(l + 1)]# 更新参数parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * v["dW" + str(l + 1)]parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * v["db" + str(l + 1)]return parameters, v
测试:
#测试update_parameters_with_momentun
print("-------------测试update_parameters_with_momentun-------------")
parameters,grads,v = testCase.update_parameters_with_momentum_test_case()
update_parameters_with_momentun(parameters,grads,v,beta=0.9,learning_rate=0.01)print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))
测试结果如下:
-------------测试update_parameters_with_momentun-------------
W1 = [[ 1.62544598 -0.61290114 -0.52907334][-1.07347112 0.86450677 -2.30085497]]
b1 = [[ 1.74493465][-0.76027113]]
W2 = [[ 0.31930698 -0.24990073 1.4627996 ][-2.05974396 -0.32173003 -0.38320915][ 1.13444069 -1.0998786 -0.1713109 ]]
b2 = [[-0.87809283][ 0.04055394][ 0.58207317]]
v["dW1"] = [[-0.11006192 0.11447237 0.09015907][ 0.05024943 0.09008559 -0.06837279]]
v["db1"] = [[-0.01228902][-0.09357694]]
v["dW2"] = [[-0.02678881 0.05303555 -0.06916608][-0.03967535 -0.06871727 -0.08452056][-0.06712461 -0.00126646 -0.11173103]]
v["db2"] = [[ 0.02344157][ 0.16598022][ 0.07420442]]
需要注意的是速度 v v v 是用 0 来初始化的,因此,该算法需要经过几次迭代才能把速度提升上来并开始跨越更大步伐。当 β = 0 \beta=0 β=0 时,该算法相当于是没有使用 momentum 算法的标准的梯度下降算法。当 β \beta β 越大的时候,说明平滑的作用越明显。通常 0.9 是比较合适的值。那如何才能在开始的时候就保持很快的速度向最小误差那里前进呢?我们来看看下面的 Adam 算法。
4. Adam 算法
Adam(Adaptive Moment Estimation)算法结合了动量梯度下降算法和RMSprop算法。其算法流程如下:
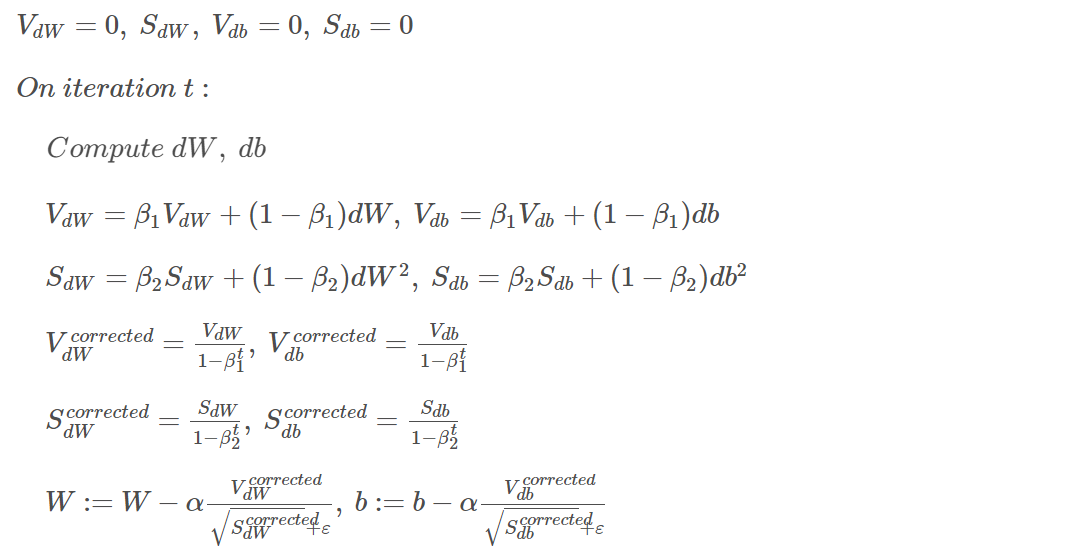
Adam算法包含了几个超参数,分别是: α , β 1 , β 2 , ϵ \alpha,\beta_1,\beta_2,\epsilon α,β1,β2,ϵ。其中, β 1 \beta_1 β1 通常设置为 0.9, β 2 \beta_2 β2 通常设置为 0.999, ϵ \epsilon ϵ 通常设置为 1 0 − 8 10^{-8} 10−8。一般只需要对 β 1 \beta_1 β1 和 β 2 \beta_2 β2 进行调试。
4.1 初始化参数
def initialize_adam(parameters):"""初始化v和s,它们都是字典类型的变量,都包含了以下字段:- keys: "dW1", "db1", ..., "dWL", "dbL" - values:与对应的梯度/参数相同维度的值为零的numpy矩阵参数:parameters - 包含了以下参数的字典变量:parameters["W" + str(l)] = Wlparameters["b" + str(l)] = bl返回:v - 包含梯度的指数加权平均值,字段如下:v["dW" + str(l)] = ...v["db" + str(l)] = ...s - 包含平方梯度的指数加权平均值,字段如下:s["dW" + str(l)] = ...s["db" + str(l)] = ..."""L = len(parameters) // 2v = {}s = {}for l in range(L):v["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])v["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])s["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])s["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])return (v, s)
测试:
#测试initialize_adam
print("-------------测试initialize_adam-------------")
parameters = testCase.initialize_adam_test_case()
v,s = initialize_adam(parameters)print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))
print('s["dW1"] = ' + str(s["dW1"]))
print('s["db1"] = ' + str(s["db1"]))
print('s["dW2"] = ' + str(s["dW2"]))
print('s["db2"] = ' + str(s["db2"]))
测试结果如下:
-------------测试initialize_adam-------------
v["dW1"] = [[0. 0. 0.][0. 0. 0.]]
v["db1"] = [[0.][0.]]
v["dW2"] = [[0. 0. 0.][0. 0. 0.][0. 0. 0.]]
v["db2"] = [[0.][0.][0.]]
s["dW1"] = [[0. 0. 0.][0. 0. 0.]]
s["db1"] = [[0.][0.]]
s["dW2"] = [[0. 0. 0.][0. 0. 0.][0. 0. 0.]]
s["db2"] = [[0.][0.][0.]]
4.2 更新参数
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate=0.01, beta1=0.9, beta2=0.999, epsilon=1e-8):"""使用Adam更新参数参数:parameters - 包含了以下字段的字典:parameters['W' + str(l)] = Wlparameters['b' + str(l)] = blgrads - 包含了梯度值的字典,有以下key值:grads['dW' + str(l)] = dWlgrads['db' + str(l)] = dblv - Adam的变量,第一个梯度的移动平均值,是一个字典类型的变量s - Adam的变量,平方梯度的移动平均值,是一个字典类型的变量t - 当前迭代的次数learning_rate - 学习率beta1 - 动量,超参数,用于第一阶段,使得曲线的Y值不从0开始(参见天气数据的那个图)beta2 - RMSprop的一个参数,超参数epsilon - 防止除零操作(分母为0)返回:parameters - 更新后的参数v - 第一个梯度的移动平均值,是一个字典类型的变量s - 平方梯度的移动平均值,是一个字典类型的变量"""L = len(parameters) // 2v_corrected = {} # 偏差修正后的值s_corrected = {} # 偏差修正后的值for l in range(L):#梯度的移动平均值,输入:"v , grads , beta1",输出:" v "v["dW" + str(l + 1)] = beta1 * v["dW" + str(l + 1)] + (1 - beta1) * grads["dW" + str(l + 1)]v["db" + str(l + 1)] = beta1 * v["db" + str(l + 1)] + (1 - beta1) * grads["db" + str(l + 1)]#计算平方梯度的移动平均值,输入:"s, grads , beta2",输出:"s"s["dW" + str(l + 1)] = beta2 * s["dW" + str(l + 1)] + (1 - beta2) * np.square(grads["dW" + str(l + 1)])s["db" + str(l + 1)] = beta2 * s["db" + str(l + 1)] + (1 - beta2) * np.square(grads["db" + str(l + 1)])#计算第一阶段的偏差修正后的估计值,输入"v , beta1 , t" , 输出:"v_corrected"v_corrected["dW" + str(l + 1)] = v["dW" + str(l + 1)] / (1 - np.power(beta1,t))v_corrected["db" + str(l + 1)] = v["db" + str(l + 1)] / (1 - np.power(beta1,t))#计算第二阶段的偏差修正后的估计值,输入:"s , beta2 , t",输出:"s_corrected"s_corrected["dW" + str(l + 1)] = s["dW" + str(l + 1)] / (1 - np.power(beta2,t))s_corrected["db" + str(l + 1)] = s["db" + str(l + 1)] / (1 - np.power(beta2,t))#更新参数,输入: "parameters, learning_rate, v_corrected, s_corrected, epsilon". 输出: "parameters".parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * (v_corrected["dW" + str(l + 1)] / (np.sqrt(s_corrected["dW" + str(l + 1)]) + epsilon))parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * (v_corrected["db" + str(l + 1)] / (np.sqrt(s_corrected["db" + str(l + 1)]) + epsilon))return (parameters, v, s)
测试:
#测试update_with_parameters_with_adam
print("-------------测试update_with_parameters_with_adam-------------")
parameters , grads , v , s = testCase.update_parameters_with_adam_test_case()
update_parameters_with_adam(parameters,grads,v,s,t=2)print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))
print('s["dW1"] = ' + str(s["dW1"]))
print('s["db1"] = ' + str(s["db1"]))
print('s["dW2"] = ' + str(s["dW2"]))
print('s["db2"] = ' + str(s["db2"]))
测试结果如下:
-------------测试update_with_parameters_with_adam-------------
W1 = [[ 1.63178673 -0.61919778 -0.53561312][-1.08040999 0.85796626 -2.29409733]]
b1 = [[ 1.75225313][-0.75376553]]
W2 = [[ 0.32648046 -0.25681174 1.46954931][-2.05269934 -0.31497584 -0.37661299][ 1.14121081 -1.09244991 -0.16498684]]
b2 = [[-0.88529979][ 0.03477238][ 0.57537385]]
v["dW1"] = [[-0.11006192 0.11447237 0.09015907][ 0.05024943 0.09008559 -0.06837279]]
v["db1"] = [[-0.01228902][-0.09357694]]
v["dW2"] = [[-0.02678881 0.05303555 -0.06916608][-0.03967535 -0.06871727 -0.08452056][-0.06712461 -0.00126646 -0.11173103]]
v["db2"] = [[0.02344157][0.16598022][0.07420442]]
s["dW1"] = [[0.00121136 0.00131039 0.00081287][0.0002525 0.00081154 0.00046748]]
s["db1"] = [[1.51020075e-05][8.75664434e-04]]
s["dW2"] = [[7.17640232e-05 2.81276921e-04 4.78394595e-04][1.57413361e-04 4.72206320e-04 7.14372576e-04][4.50571368e-04 1.60392066e-07 1.24838242e-03]]
s["db2"] = [[5.49507194e-05][2.75494327e-03][5.50629536e-04]]
二、测试
1. 加载数据集
我们使用下面的“月亮(moon)”数据集来测试不同的优化方法。数据集被命名为“月亮”,因为这两个类的数据看起来有点像新月形的月亮。
train_X, train_Y = opt_utils.load_dataset()
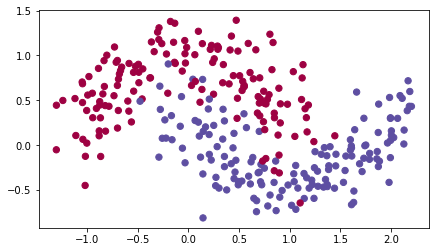
2. 定义模型
def model(X, Y, layers_dims, optimizer, learning_rate=0.0007,mini_batch_size=64, beta=0.9, beta1=0.9, beta2=0.999,epsilon=1e-8, num_epochs=10000, print_cost=True, is_plot=True):"""可以运行在不同优化器模式下的3层神经网络模型。参数:X - 输入数据,维度为(2,输入的数据集里面样本数量)Y - 与X对应的标签layers_dims - 包含层数和节点数量的列表optimizer - 字符串类型的参数,用于选择优化类型,【 "gd" | "momentum" | "adam" 】learning_rate - 学习率mini_batch_size - 每个小批量数据集的大小beta - 用于动量优化的一个超参数beta1 - 用于计算梯度后的指数衰减的估计的超参数beta1 - 用于计算平方梯度后的指数衰减的估计的超参数epsilon - 用于在Adam中避免除零操作的超参数,一般不更改num_epochs - 整个训练集的遍历次数,(视频2.9学习率衰减,1分55秒处,视频中称作“代”),相当于之前的num_iterationprint_cost - 是否打印误差值,每遍历1000次数据集打印一次,但是每100次记录一个误差值,又称每1000代打印一次is_plot - 是否绘制出曲线图返回:parameters - 包含了学习后的参数"""L = len(layers_dims)costs = []t = 0 # 每学习完一个 mini-batch 就增加 1seed = 10# 初始化参数parameters = opt_utils.initialize_parameters(layers_dims)# 选择优化器if optimizer == "gd":pass # 不使用任何优化器,直接用梯度下降法elif optimizer == "momentum":v = initialize_velocity(parameters) # 使用momentumelif optimizer == "adam":v, s = initialize_adam(parameters) # 使用Adam优化else:print("optimizer参数错误,程序退出。")exit(1)# 开始学习for i in range(num_epochs):#定义随机 minibatches,我们在每次遍历数据集之后增加种子以重新排列数据集,使每次数据的顺序都不同seed = seed + 1minibatches = random_mini_batches(X, Y, mini_batch_size, seed)for minibatch in minibatches:# 选择一个 minibatch(minibatch_X, minibatch_Y) = minibatch# 前向传播A3, cache = opt_utils.forward_propagation(minibatch_X, parameters)# 计算误差cost = opt_utils.compute_cost(A3, minibatch_Y)# 反向传播grads = opt_utils.backward_propagation(minibatch_X, minibatch_Y, cache)# 更新参数if optimizer == "gd":parameters = update_parameters_with_gd(parameters,grads,learning_rate)elif optimizer == "momentum":parameters, v = update_parameters_with_momentum(parameters,grads,v,beta,learning_rate)elif optimizer == "adam":t = t + 1 parameters , v , s = update_parameters_with_adam(parameters,grads,v,s,t,learning_rate,beta1,beta2,epsilon)# 记录误差值if i % 100 == 0:costs.append(cost)#是否打印误差值if print_cost and i % 1000 == 0:print("第" + str(i) + "次遍历整个数据集,当前误差值:" + str(cost))#是否绘制曲线图if is_plot:plt.plot(costs)plt.ylabel('cost')plt.xlabel('epochs (per 100)')plt.title("Learning rate = " + str(learning_rate))plt.show()return parameters
3. 测试
3.1 使用梯度下降算法
layers_dims = [train_X.shape[0],5,2,1]
parameters = model(train_X, train_Y, layers_dims, optimizer="gd",is_plot=True)
运行结果:
第0次遍历整个数据集,当前误差值:0.690735512291113
第1000次遍历整个数据集,当前误差值:0.6852725328458241
第2000次遍历整个数据集,当前误差值:0.6470722240719003
第3000次遍历整个数据集,当前误差值:0.6195245549970402
第4000次遍历整个数据集,当前误差值:0.5765844355950945
第5000次遍历整个数据集,当前误差值:0.6072426395968576
第6000次遍历整个数据集,当前误差值:0.5294033317684576
第7000次遍历整个数据集,当前误差值:0.46076823985930115
第8000次遍历整个数据集,当前误差值:0.465586082399045
第9000次遍历整个数据集,当前误差值:0.4645179722167684
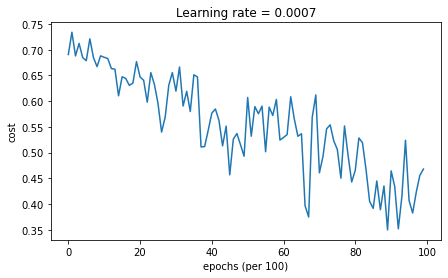
绘制分类结果图:
preditions = opt_utils.predict(train_X,train_Y,parameters)#绘制分类图
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-1, 1.5])
opt_utils.plot_decision_boundary(lambda x: opt_utils.predict_dec(parameters, x.T), train_X, train_Y)
运行结果如下:
Accuracy: 0.7966666666666666
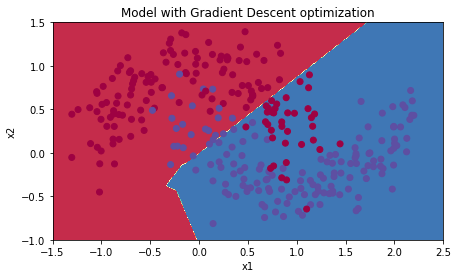
3.2 使用动量梯度下降算法```c
layers_dims = [train_X.shape[0],5,2,1]
parameters = model(train_X, train_Y, layers_dims, beta=0.9,optimizer=“momentum”,is_plot=True)
运行结果:
```c
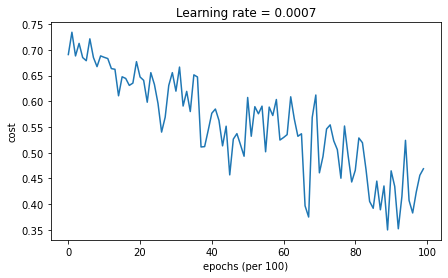
第0次遍历整个数据集,当前误差值:0.6907412988351506
第1000次遍历整个数据集,当前误差值:0.6853405261267578
第2000次遍历整个数据集,当前误差值:0.6471448370095255
第3000次遍历整个数据集,当前误差值:0.6195943032076022
第4000次遍历整个数据集,当前误差值:0.5766650344073023
第5000次遍历整个数据集,当前误差值:0.607323821900647
第6000次遍历整个数据集,当前误差值:0.5294761758786997
第7000次遍历整个数据集,当前误差值:0.46093619004872366
第8000次遍历整个数据集,当前误差值:0.465780093701272
第9000次遍历整个数据集,当前误差值:0.4647395967922748
绘制分类结果图:
preditions = opt_utils.predict(train_X,train_Y,parameters)#绘制分类图
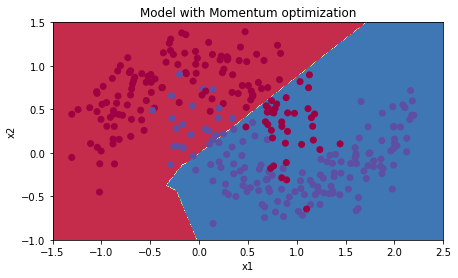
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-1, 1.5])
opt_utils.plot_decision_boundary(lambda x: opt_utils.predict_dec(parameters, x.T), train_X, train_Y)
运行结果如下:
Accuracy: 0.7966666666666666
3.3 使用Adam算法
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer="adam",is_plot=True)
运行结果:
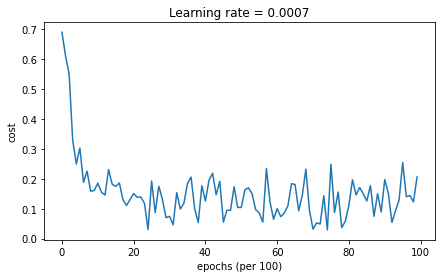
第0次遍历整个数据集,当前误差值:0.6905522282919487
第1000次遍历整个数据集,当前误差值:0.1855671862856554
第2000次遍历整个数据集,当前误差值:0.1508520614524249
第3000次遍历整个数据集,当前误差值:0.07445357759814121
第4000次遍历整个数据集,当前误差值:0.12593575021785638
第5000次遍历整个数据集,当前误差值:0.10423511812705895
第6000次遍历整个数据集,当前误差值:0.10055245705471472
第7000次遍历整个数据集,当前误差值:0.031601421953614484
第8000次遍历整个数据集,当前误差值:0.11170898322507423
第9000次遍历整个数据集,当前误差值:0.19764808191072578
绘制分类结果图:
preditions = opt_utils.predict(train_X,train_Y,parameters)#绘制分类图
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-1, 1.5])
opt_utils.plot_decision_boundary(lambda x: opt_utils.predict_dec(parameters, x.T), train_X, train_Y)
运行结果如下:
Accuracy: 0.94
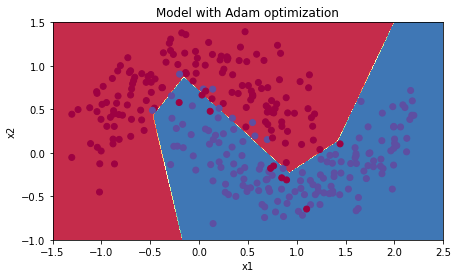
3.4 总结
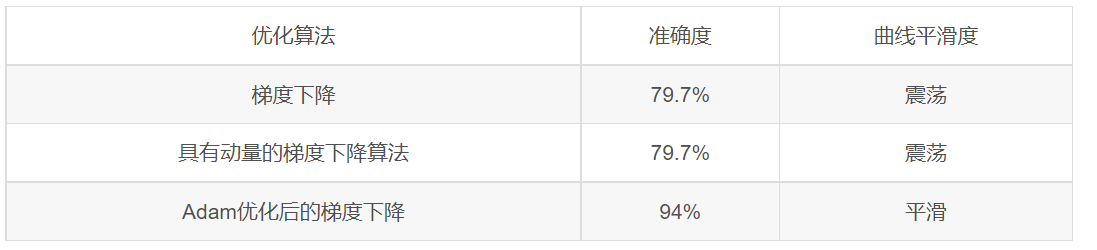
具有动量的梯度下降通常可以有很好的效果,但由于小的学习速率和简单的数据集所以它的影响几乎是轻微的。另一方面,Adam明显优于小批量梯度下降和具有动量的梯度下降,如果在这个简单的模型上运行更多时间的数据集,这三种方法都会产生非常好的结果,然而,我们已经看到Adam收敛得更快。
Adam的一些优点包括相对较低的内存要求(虽然比梯度下降和动量下降更高)和通常运作良好,即使对参数进行微调(除了学习率 α \alpha α)