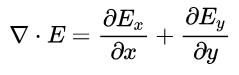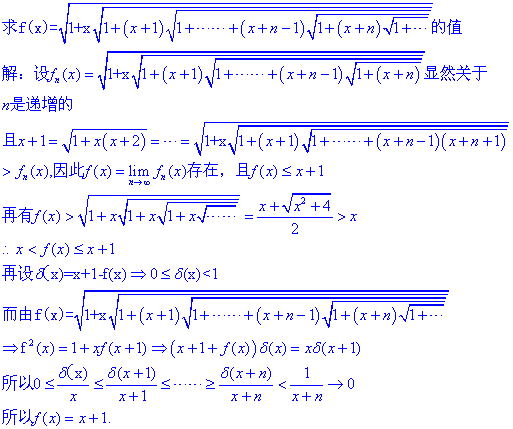相关文章
高考数学复习重点:简单的三角恒等变换(解析及答案)-图文
本文作者:vxbomath 大家好,今天分享高考数学复习三角恒等变换习题,通过解析及答案讲解,快速掌握高中数学三角恒等变换。
一、选择题 二、填空题 三、解答题 今天分享高考数学复习三角恒等变换到这里了,本文章有电子…
叉积 微分 恒等式_最美的公式:你也能懂的麦克斯韦方程组(微分篇)(下)...
上篇:最美的公式:你也能懂的麦克斯韦方程组(微分篇)(上) 11梯度、散度和旋度 ▽算子不是一个矢量,除非你把它作用在一个函数上,否则它没啥意义。但是,它在各个方面的表现确实又像一个矢量,只要你把▽算子的“作用”看成矢量的“相乘”。 一个矢量一般来说有3种“乘法”:…
matlab 拉马努金恒等,广州恒大海报谜底:拉马努金恒等式:欧拉公式
广州恒大在今年的亚冠中大出风头,打入决赛,在首尔客场也战平的韩国首尔FC,这给了一直处于寒冬中的中国足球带了了一丝的希望。连我这个“伪球迷”最近也开始关注恒大的比赛了(国足的比赛,我早戒了!)。11月9日的主场亚冠…
Prefix Sum —— 树状数组+懵逼的组合恒等式
链接:https://www.nowcoder.com/acm/contest/147/H 来源:牛客网
Niuniu has learned prefix sum and he found an interesting about prefix sum.
Let’s consider (k1) arrays a[i] (0 < i < k) The index of a[i] starts from 1. a[i] is a…
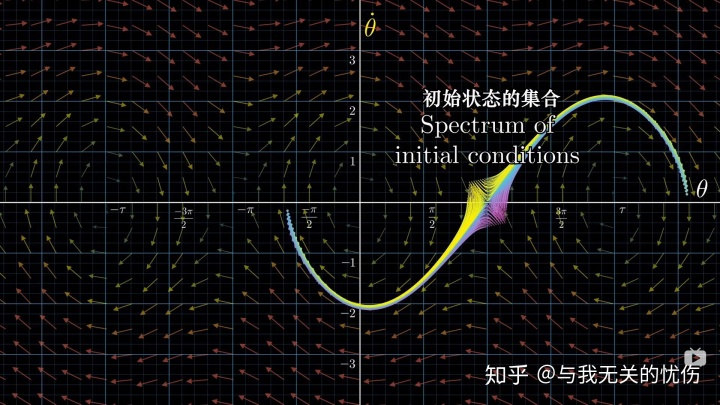
叉积 微分 恒等式_单摆-微分方程浅谈
引子[1] 单摆,这个在中学物理都学过的东西,应该是非常熟悉了。 图片来源-维基百科 小角度简单摆 若最高处( )的绳子和最低处(速度最大值)的绳子的角度为 ,则可使用下列公式算出它的振动周期。 公式证明 摆球受力分析 绳与对称线夹角为 &…
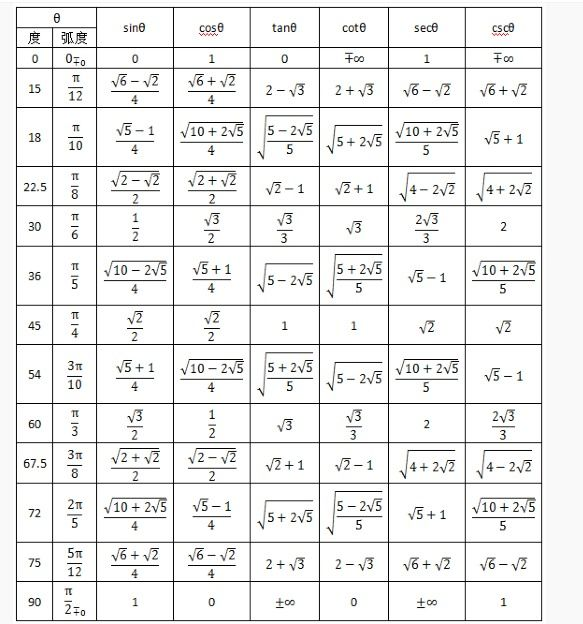
三角学常见公式定理证明
前置知识
(1)毕达哥拉斯定理: sin 2 α cos 2 β 1 \sin^2\alpha\cos^2\beta1 sin2αcos2β1
(2)诱导公式: sin ( 2 k π α ) sin α , cos ( 2 k π α ) cos α , ( k ∈ Z )…
一个由三角形引出的乘积恒等式
故事背景 故事发生在我考完试后的第二天,我正躺在床上悠闲着耍着我的最右,突然一个神秘的黑色图片映入我的眼帘。我盯着看了一段时间,发现这明显是在挑衅我啊,我好歹也是经历过高考的人的,你就拿这种题愚弄我ÿ…
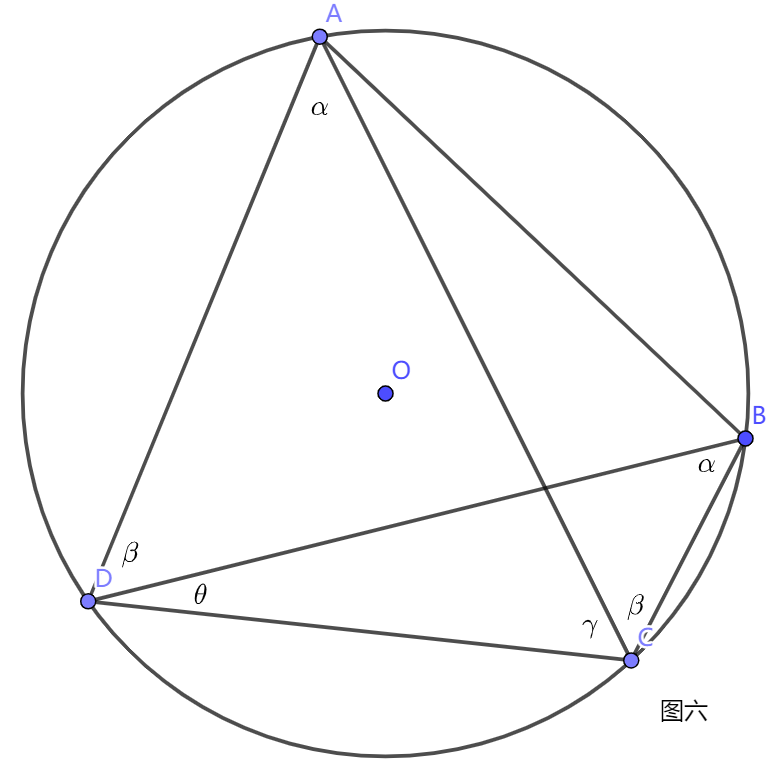
HDU 3903 Trigonometric Function (三角恒等式余弦定理)
http://acm.hdu.edu.cn/showproblem.php?pid3903 如何判断的有理性? 由这三个式子: 问题可化归为判断A,B,C的正弦和余弦是否为有理数,又由余弦定理 以及 cos(arccos x)x 若xp/q,则sqrt(1-x^2)sqrt(q^2-p^2)/q 故只需判断q^2-p^2是…
math_角函数反三角函数诱导公式三角/反三角恒等式@三角函数微积分
[toc]
三角函数
图像
图像:六种基本的三角函数图像🎈 三角函数的基本内涵 三角函数(英语:Trigonometric functions)是数学中常见的一类关于角度的函数。 三角函数将直角三角形的内角与它的两个边的比值相关联,也可以等价地用与…
2.三角函数基础2(普林斯顿微积分笔记)
2021.10.13
一、三角恒等式 基本恒等公式 t a n ( θ ) s i n ( θ ) c o s ( θ ) tan(\theta){sin(\theta)\over cos(\theta)} tan(θ)cos(θ)sin(θ) 毕达哥拉斯定理公式(勾股定理) a 2 b 2 c 2 a^2b^2c^2 a2b2c2 s i n 2 ( α ) c o s 2 …
jdk环境配置没问题eclipse打不开出现Incompatible JVM错误
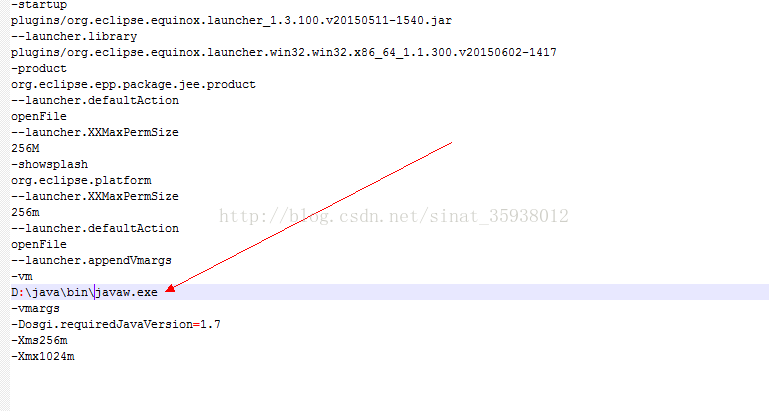
报错 Incompatible JVM version 1.8.0_271 of the VM is not suitable for this product.Version:11 or greater is required. 打开eclipse安装位置 打开eclipse.ini,添加jdk路径 -vm E:\javaJDK\Java\jdk-15.0.1\bin
修改jdk路径重新配置环境变量,导致eclipse打不开
转自:https://blog.csdn.net/sinat_35938012/article/details/76652755 A Java Runtime Environment(JRE) or java Development Kit(JDK) must be available in order to run Eclipse. No java virtual machine was found after searching the folloing locations; …
eclipse因jdk打不开解决
1.更换window的jdk版本 (1)环境变量配置 右击“我的电脑”,选择“属性”,再选择“高级系统设置”,如下图 ,之后在点击上图中的“环境变量”,进入配置页,如图 ,选中系统变…
eclipse打不开的问题
大家都知道Eclipse是开发源代码平台,在使用中也难免会遇到一些错误问题,有用户在更换jdk版本或配置较多个jdk版本原因,在打开Eclipse时提示错误信息,failed to create the java virtual machine(如下图所示)导致无法正常打开&…