11梯度、散度和旋度

▽算子不是一个矢量，除非你把它作用在一个函数上，否则它没啥意义。但是，它在各个方面的表现确实又像一个矢量，只要你把▽算子的“作用”看成矢量的“相乘”。

一个矢量一般来说有3种“乘法”：

1、矢量A和一个标量a相乘：aA。比如我把一个矢量A大小变为原来的2倍，方向不变，那么这时候就可以写成2A。

2、矢量A和一个矢量B进行点乘：A·B。这个点乘我们上面介绍很多了，A·B=|A||B|Cosθ，这里就不说了。

3、矢量A和一个矢量B进行叉乘：A×B。这个叉乘跟点乘类似，也是我们单独针对矢量定义的另外一种乘法，A×B=|A||B|Sinθ。大家可以看到，这个叉乘跟点乘唯一的区别就是：点乘是两个矢量的大小乘以它们的余弦值Cosθ，叉乘是两个矢量的大小乘以它们的正弦值Sinθ(在直角三角形里，角的对边和斜边的比为正弦Sinθ，邻边和斜边的比值为余弦Cosθ)。

那么，同样的，我们的▽算子也有3种作用方式：

1、▽算子作用在一个标量函数z上：▽z。这个▽z我们上面说过了，它表示函数z的梯度，它表示这个函数z变化最快的方向。

2、▽算子跟一个矢量函数E点乘：▽·E。这就表示E的散度，我们开篇讲的高斯电场定律的左边就是电场E的散度，它就是表示成▽·E这样。

3、▽算子跟一个矢量函数E叉乘：▽×E。它叫E的旋度，这个我们后面会再详细说。

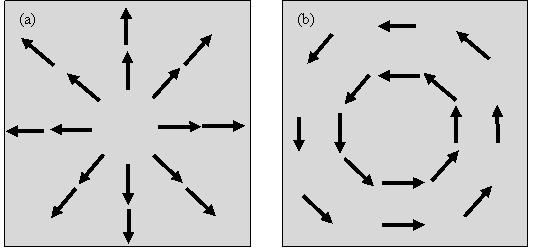
这样，我们就以一种很自然的方式引出了这三个非常重要的概念：梯度(▽z)、散度(▽·E)和旋度(▽×E)。大家可以看到，▽算子的这三种作用跟矢量的三种乘法是非常相似的，只不过▽是一个算子，它必须作用在一个函数上才行，所以我们把上面的标量和矢量换成了标量函数和矢量函数。

我们在描述山的高度的函数z=f(x,y)的时候，不同的点(x,y)对应不同的山的高度，而山的高度只有大小没有方向，所以这是个标量函数，我们可以求它的梯度▽z。但是，电场E既有大小又有方向，这是一个矢量，所以我们可以用一个矢量函数E=f(x,y)表示空间中不同点(x,y)的电场E的分布情况。那么对这种矢量函数，我们就不能去求它的梯度了，我们只能去求它的散度▽·E和旋度▽×E。

为了让大家对这些能够有更直观的概念，我们接下来就来仔细看看电场的散度▽·E。

12电场的散度

当我们把电场的散度写成▽·E这样的时候，我们会觉得：啊，好简洁！但是我们也知道▽算子的定义是这样的：

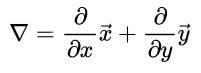
那么▽·E就应该写成这样：

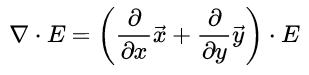
而我们知道电场E其实是一个矢量函数(不同点对应的电场的情况)，那我们还是可以把E分解成x,y两个分量的和，这两个分量后面跟一个x和y方向的单位向量就行了。那么，上面的式子就可以写成这样：

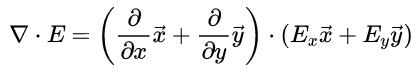
然后，因为矢量点乘是满足分配律的，所以我们可以把他们按照普通乘法一样展开成四项。而x和y是垂直的单位向量，所以x·y=y·x=0，x·x=y·y=1，然后我们最后剩下的就只有这两项了(这一块的推导逻辑跟“坐标系下的矢量点乘”那一节一样，觉得有点陌生的可以再返回去看看那一部分)：

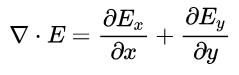
这就是电场E的散度的最终表达式，它的意思很明显：我们求电场E的散度就是把矢量函数E分解成x和y方向上的两个函数，然后分别对它们求偏导，最后再把结果加起来就行了。

为了让大家对这个有个更直观的概念，我们来看两个小例子：

例1：求函数y=2x+1的导数。

这个函数的图像是一条直线(不信的可以自己去找一些x的值，代入进去算算y的值，然后把这些点画在图上)，它的斜率是2，也就是说导数是2。也就是说，对于一次函数(最多只有x，没有x的平方、立方……)，它的导数就是x前面的系数(2x前面的2)，而后面的常数(1)对导数没有任何影响。

例2：求电场E=2x+yy的散度。

我们先来看看这个电场E，它在x方向上(2x)的系数是2，也就是说它的电场强度是不变的，一直都是2。但是，在y方向上(yy)的系数是y，也就是说当我越来越远离y轴的时候，这个系数y也会越来越多，这就表示y方向上的电场强度会越来越大。

所以E=2x+yy描述的是这样一个在x轴方向上不变，在y轴方向上不断变大的电场。要求这个电场的散度，根据上面的式子，我们得先求出电场的偏导数，那偏导数要怎么求呢？还记得我们是怎么得到偏导数这个概念的么？我们是固定y的值，也就是假设y的值不变，把y看作一个常数，这时候求得了对x的偏导数；同样，把x当做一个常数，求函数对y的偏导数。

那么，当我们求函数对x的偏导数∂E/∂x时，我们可以把y当作常数(就像例1中后面的1一样)。如果y是常数，x方向前面的系数又是2，也是常数，所以这整个就变成了一个常数(常数的导数为0)，所以∂E/∂x=0。同样，当我们求y的偏导的时候，就把x都看成常数(导数为0)，而y方向前面的系数为y(导数为1)，所以∂E/∂y=0+1=1。

那么电场E的散度▽·E就可以表示成这两个偏导数的和：▽·E=∂E/∂x+∂E/∂y=0+1=1，也就是说，电场E的散度为1。

这虽然是一个非常简单的求电场散度的例子，但是却包含了我们求偏导，求散度的基本思想。通过这种方式，我们可以很轻松的就把电场E的散度▽·E求出来了。

补了这么多的数学和推导，我们现在有了一个定义良好，计算方便的散度▽·表达式了，但是，你还记得我们在开始讲到的散度的定义么？我们最开始是怎样引入散度的呢？

我们是从麦克斯韦方程组的积分形式引入散度</