引子[1]
单摆,这个在中学物理都学过的东西,应该是非常熟悉了。
图片来源-维基百科 小角度简单摆
若最高处(
![]()
)的绳子和最低处(速度最大值)的绳子的角度为
![]()
,则可使用下列公式算出它的振动周期。
公式证明
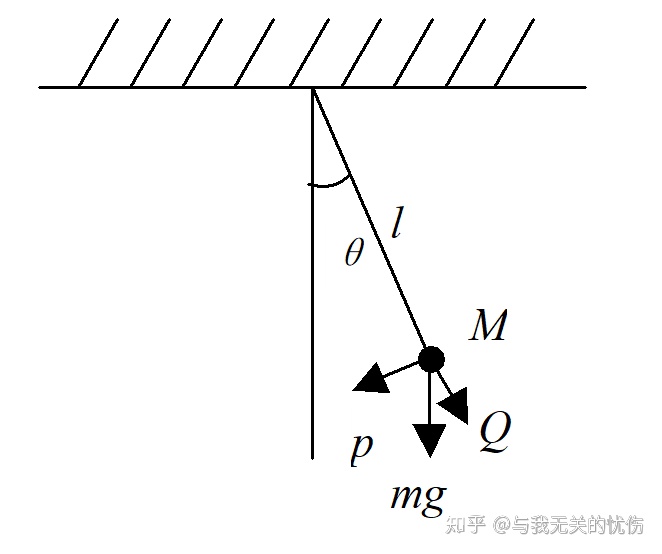
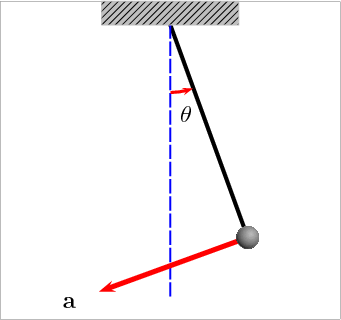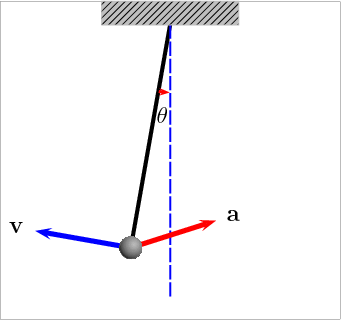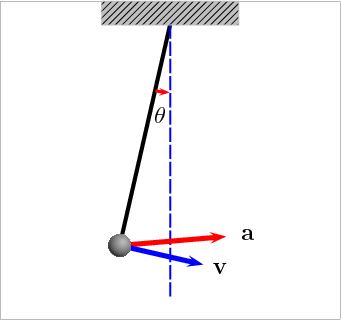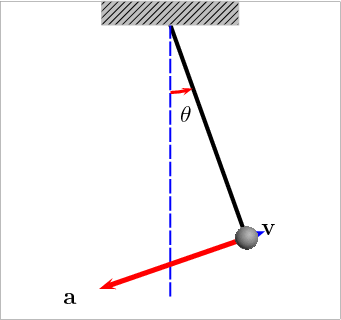
摆球受力分析 绳与对称线夹角为
![]()
,绳长为
![]()
,绳距离对称线的水平距离为
![]()
。对于处在某一点的小球进行受力分析,小球受到的力只有重力和拉力。
![]()
,这个力指向平衡位置,称为回复力。
由于
![]()
很小,所以有近似
![]()
,所以有下列成立
![]()
,令
下面推导弹簧的周期公式(如果知道直接跳过)
弹簧简谐振动 设弹簧的弹性系数为
![]()
,弹簧距离平衡点的距离为
![]()
,对于简谐振动的弹簧,有
![]()
,将其与上式联立,有
![]()
,根据三角函数的周期公式,有
回到单摆的话题上来
刚刚推导的回复力
![]()
,代入公式弹簧的周期公式,得到
这是中学时候的单摆公式的推导,看得出,主要是由于条件
![]()
这个条件限制产生的
![]()
所导致的,下面来看看一般情况下的单摆,也就是任意条件的
![]()
。
一般情况下的单摆
设与对称线的夹角为
![]()
,绳子的长度为
![]()
,球的角加速度为
![]()
,忽略空气阻力由受力分析,根据牛顿第二运动定理,有
![]()
。根据角加速度和(线)加速度之间的关系
[2],有下列微分方程成立
![]()
(右边取负号是因为回复力的方向)
图片来源-百度百科 如果
![]()
,根据Taylor展开式,
![]()
,,所以对于充分小的
![]()
,有
![]()
,使用Taylor展开来理解和使用极限来理解是一样的。
求解特殊情况,微分方程
![]()
,这是一个二阶常系数齐次微分方程,
1.猜测解法
移项
![]()
,从这个等式可以看出,函数
![]()
经过两次微分之后,除了除了系数及其前面的±号改变了,本身并没有发生其他改变,对于微分之后本身还不变的函数,很容易想到余弦函数,令
![]()
,其中
![]()
为常数。
对
![]()
,求二阶导,代入微分方程,
![]()
,即
周期为
![]()
,跟前面一致。
2.公式解法
微分方程
![]()
,形如
![]()
,存在通用解法。
特征方程为
![]()
,这是一对共轭复根:对复数
![]()
,
![]()
。根为
![]()
, 通解为
![]()
,即
![]()
,
令
![]()
,
![]()
,由于
![]()
,那么肯定有
![]()
,可以化为
根据上面的结果,也可轻松知道周期为
求解一般情况,微分方程
能量守恒视角看待问题
这个方程求解比较麻烦,下面换个思路,通过能量守恒的方式来看这个问题。该系统的自由度为
![]()
,使用广义坐标
![]()
来描述
[3]。设系统动能为
![]()
,系统势能为
![]()
,小球质量为
![]()
,绳长
![]()
,不计绳质量。取摆点最低处为零势能点。
从上式计算角速度
从这个式子里面可以看到,
![]()
都是常数,是因变量角速度
![]()
与自变量角度
![]()
的函数关系。下面来讨论一下这个式子,令
得到式子为
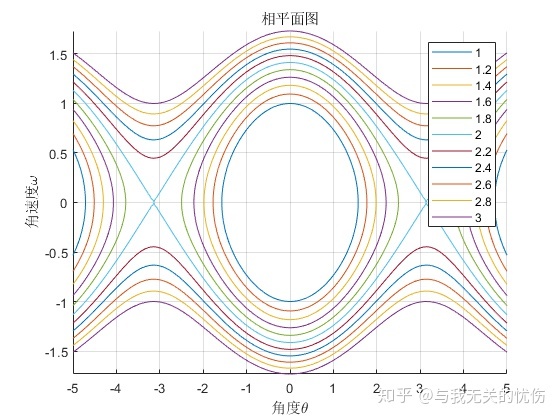
角度和角速度之间的关系,图标对应的是不同的e的值 上图研究了角度与角速度之间的关系,这样的图叫做相平面图。从上面图可以看出
![]()
由于能量不足,摆仅做平衡位置附近的周期运动。
![]()
是一种临界状态,相当于摆锤摆到最高位置的过程。
![]()
能量过大,而使摆角的绝对值随时间之增加而无限增加,对应于摆绕支点无穷次旋转的运动过程。
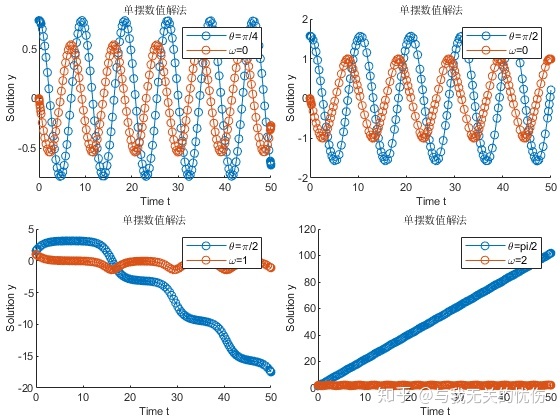
微分方程数值解法
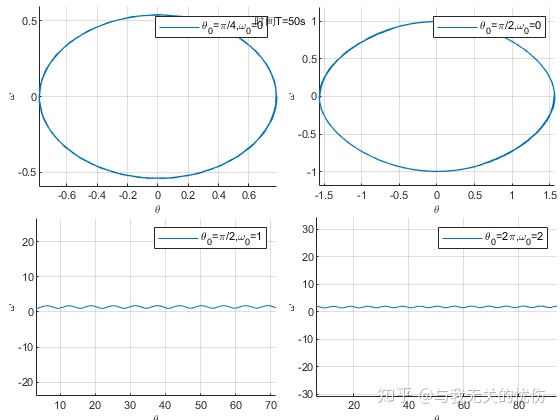
微分方程计算的相平面图 求解的时域图 在求解上面的微分方程的时候,使用的方法是
![]()
公式 。具体求解过程可以参考MATLAB的帮助文档和参考书
[4]。
带阻尼的单摆
下面来看看带阻尼的单摆是怎么使用的其实在求解上面的代码里面就已经加入空气阻力一项了,只不过将其值设为了0,下面来看看改变这个值会发生什么。一般来说,空气阻力公式为
这里设
![]()
,
![]()
为阻尼因子。
那么上面的微分方程变为
跟上面一样将,使用
![]()
求解。
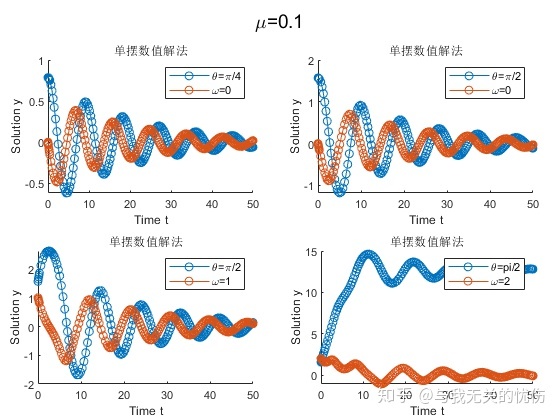
时域图
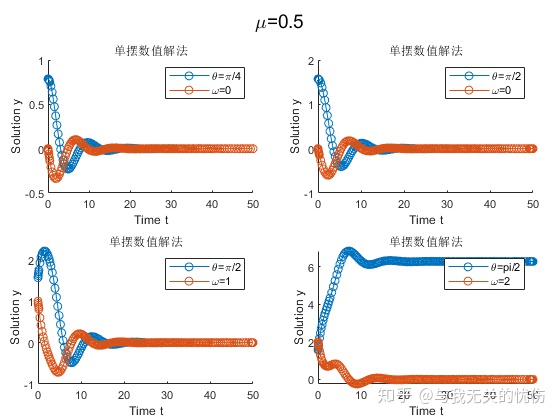
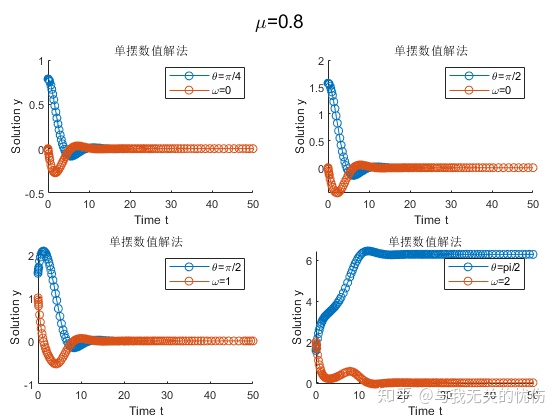
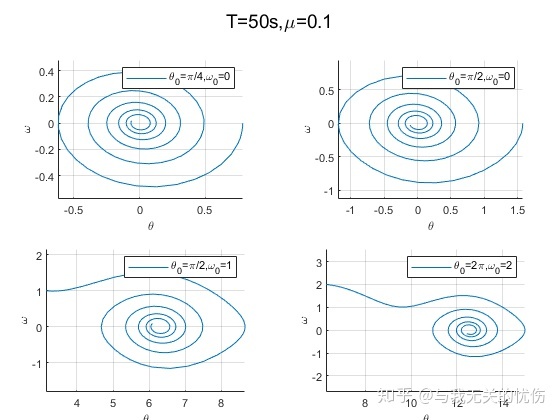
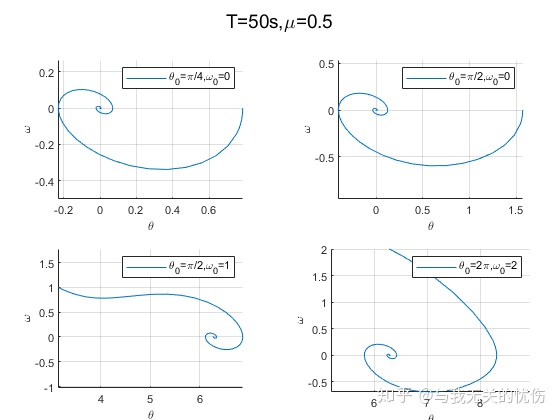
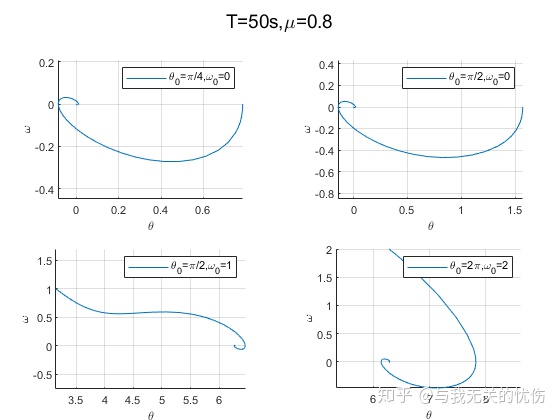
时间T=50s,阻力系数μ=0.1 时间T=50s,阻力系数μ=0.5 时间T=50s,阻力系数μ=0.8 相平面图
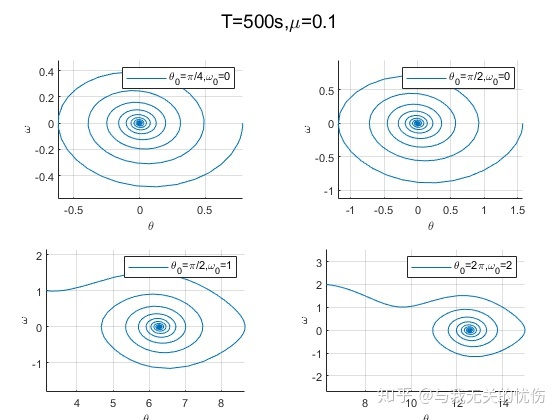
时间T=500s,阻力系数μ=0.1 时间T=50s,阻力系数μ=0.1 时间T=50s,阻力系数μ=0.5 时间T=50s,阻力系数μ=0.8 从上面这些图来看,加入空气阻力之后确实是一种带阻尼的震动图像的样子。并且阻尼越大,能量耗散的也越快。
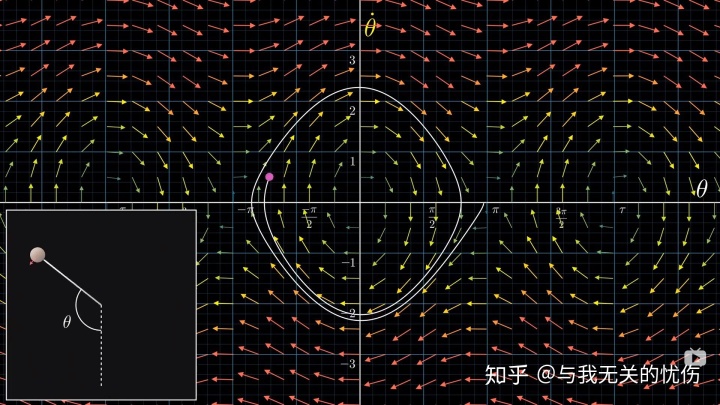
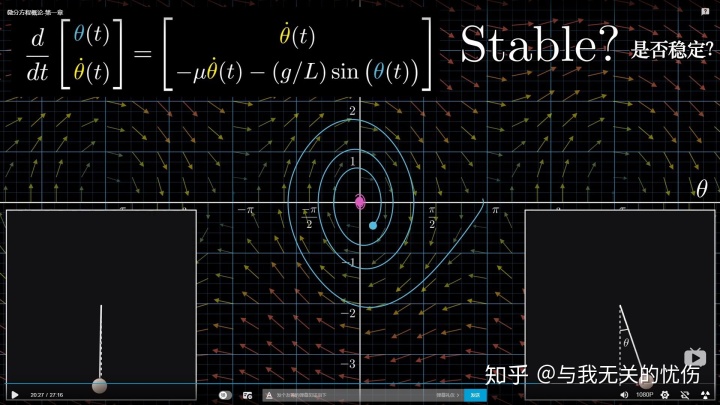
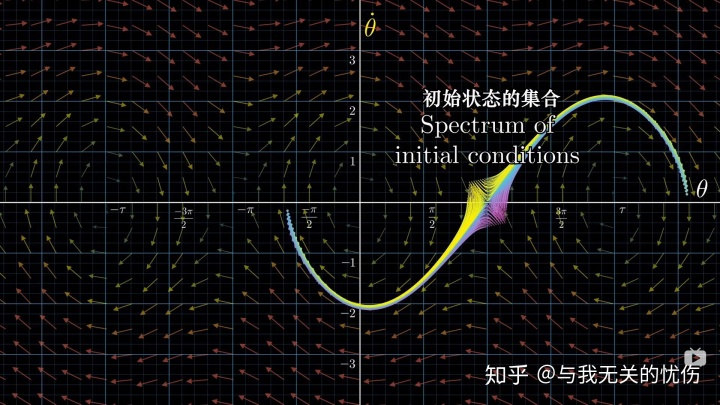
最后,其实要说的是,强烈推荐这个视频。其实前面所有讨论的东西都在下面的几张图里面了,可以回味回味。
代码
隐函数画图代码
微分方程数值解代码
求解的时域图
参考
- ^单摆-维基百科 https://zh.wikipedia.org/wiki/%E6%93%BA
- ^理论力学-哈工大 https://book.douban.com/subject/3866935/
- ^力学-朗道 https://book.douban.com/subject/2059252/
- ^数值方法 https://book.douban.com/subject/4780614/