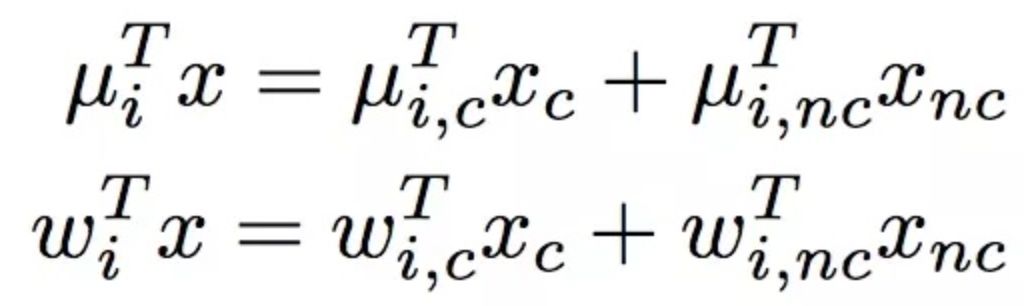推荐广告之－MLR学习

article/2025/11/9 19:52:51

算法简介：
该算法是阿里的盖坤大神力作：Learning Piece-wise Linear Models from Large Scale Data for Ad Click Prediction，介绍了阿里广告的一个主要ctr预估模型Large Scale Piece-wise Linear Model (LS-PLM)，在2012年就开始使用，据说早期叫做Mixture of LR(MLR)。

代码地址在：　　https://github.com/CastellanZhang/alphaPLM

算法介绍：http://castellanzhang.github.io/2017/06/01/mlr_plm/
以上git和博客对mlr 做出详细的介绍，本文主要介绍在学习和实践中的一些领悟，能力一般，水平有限，望路过大神多多指教．
在使用中发现，使用该算法生成模型，会产生大量的训练参数，造成实际生产中资源使用不足的问题，以个人使用的数据训练，每天训练集的特征数据大约8kw（已经经过特征筛选过滤）,训练piece_num=12(训练参数，影响参数数量)，模型40-50G,（这对于我等小集群，完全扛不住），怎么办呢？？？
就在此时，一小胖从旁走过，手拿鸡翅，汉堡，如此之人不瘦怎行！！！感叹至此，令我不禁怀想，如此之模型，不瘦身让我如何部署？想到此处，模型瘦身之念顿起。那如何瘦身嗫？
业内大佬有云“模型瘦身，首看普瑞狄特（predict），在看权零”。此话不虚，见mlr 之 predict 如下：

在#ifndef FTRL_MODEL_H_
#define FTRL_MODEL_H_#include <unordered_map>
#include <string>
#include <vector>
#include <mutex>
#include <iostream>
#include <cmath>
#include "../Utils/utils.h"using namespace std;//每一个特征维度的模型单元
class ftrl_model_unit
{
public:vector<double> u;vector<double> u_n;vector<double> u_z;vector<double> w;vector<double> w_n;vector<double> w_z;mutex mtx;
public:ftrl_model_unit(int piece_num, double u_mean, double u_stdev, double w_mean, double w_stdev){u.resize(piece_num);u_n.resize(piece_num);u_z.resize(piece_num);for(int f = 0; f < piece_num; ++f){u[f] = utils::gaussian(u_mean, u_stdev);u_n[f] = 0.0;u_z[f] = 0.0;}w.resize(piece_num);w_n.resize(piece_num);w_z.resize(piece_num);for(int f = 0; f < piece_num; ++f){w[f] = utils::gaussian(w_mean, w_stdev);w_n[f] = 0.0;w_z[f] = 0.0;}}ftrl_model_unit(int piece_num, const vector<string>& modelLineSeg){u.resize(piece_num);u_n.resize(piece_num);u_z.resize(piece_num);w.resize(piece_num);w_n.resize(piece_num);w_z.resize(piece_num);for(int f = 0; f < piece_num; ++f){u[f] = stod(modelLineSeg[1 + f]);w[f] = stod(modelLineSeg[piece_num + 1 + f]);u_n[f] = stod(modelLineSeg[2 * piece_num + 1 + f]);w_n[f] = stod(modelLineSeg[3 * piece_num + 1 + f]);u_z[f] = stod(modelLineSeg[4 * piece_num + 1 + f]);w_z[f] = stod(modelLineSeg[5 * piece_num + 1 + f]);}}void reinit_u(double u_mean, double u_stdev){int size = u.size();for(int f = 0; f < size; ++f){u[f] = utils::gaussian(u_mean, u_stdev);}}void reinit_w(double w_mean, double w_stdev){int size = w.size();for(int f = 0; f < size; ++f){w[f] = utils::gaussian(w_mean, w_stdev);}}friend inline ostream& operator <<(ostream& os, const ftrl_model_unit& mu){if(mu.u.size() > 0){os << mu.u[0];}for(int f = 1; f < mu.u.size(); ++f){os << " " << mu.u[f];}for(int f = 0; f < mu.w.size(); ++f){os << " " << mu.w[f];}for(int f = 0; f < mu.u_n.size(); ++f){os << " " << mu.u_n[f];}for(int f = 0; f < mu.w_n.size(); ++f){os << " " << mu.w_n[f];}for(int f = 0; f < mu.u_z.size(); ++f){os << " " << mu.u_z[f];}for(int f = 0; f < mu.w_z.size(); ++f){os << " " << mu.w_z[f];}return os;}
};class ftrl_model
{
public:ftrl_model_unit* muBias;unordered_map<string, ftrl_model_unit*> muMap;int piece_num;double u_stdev;double u_mean;double w_stdev;double w_mean;public:ftrl_model(double _piece_num);ftrl_model(double _piece_num, double _u_mean, double _u_stdev, double _w_mean, double _w_stdev);ftrl_model_unit* getOrInitModelUnit(string index);ftrl_model_unit* getOrInitModelUnitBias();double get_uTx(const vector<pair<string, double> >& x, ftrl_model_unit& muBias, vector<ftrl_model_unit*>& theta, int f);double get_wTx(const vector<pair<string, double> >& x, ftrl_model_unit& muBias, vector<ftrl_model_unit*>& theta, int f);double get_uTx(const vector<pair<string, double> >& x, ftrl_model_unit& muBias, unordered_map<string, ftrl_model_unit*>& theta, int f);double get_wTx(const vector<pair<string, double> >& x, ftrl_model_unit& muBias, unordered_map<string, ftrl_model_unit*>& theta, int f);double getScore(const vector<pair<string, double> >& x, ftrl_model_unit& muBias, unordered_map<string, ftrl_model_unit*>& theta);void outputModel(ofstream& out);bool loadModel(ifstream& in);void debugPrintModel();private:double get_uif(unordered_map<string, ftrl_model_unit*>& theta, const string& index, int f);double get_wif(unordered_map<string, ftrl_model_unit*>& theta, const string& index, int f);
private:mutex mtx;mutex mtx_bias;
};ftrl_model::ftrl_model(double _piece_num)
{piece_num = _piece_num;u_mean = 0.0;u_stdev = 0.0;w_mean = 0.0;w_stdev = 0.0;muBias = NULL;
}ftrl_model::ftrl_model(double _piece_num, double _u_mean, double _u_stdev, double _w_mean, double _w_stdev)
{piece_num = _piece_num;u_mean = _u_mean;u_stdev = _u_stdev;w_mean = _w_mean;w_stdev = _w_stdev;muBias = NULL;
}ftrl_model_unit* ftrl_model::getOrInitModelUnit(string index)
{unordered_map<string, ftrl_model_unit*>::iterator iter = muMap.find(index);if(iter == muMap.end()){mtx.lock();ftrl_model_unit* pMU = new ftrl_model_unit(piece_num, u_mean, u_stdev, w_mean, w_stdev);muMap.insert(make_pair(index, pMU));mtx.unlock();return pMU;}else{return iter->second;}
}ftrl_model_unit* ftrl_model::getOrInitModelUnitBias()
{if(NULL == muBias){mtx_bias.lock();muBias = new ftrl_model_unit(piece_num, 0, 0, 0, 0);mtx_bias.unlock();}return muBias;
}double ftrl_model::get_uTx(const vector<pair<string, double> >& x, ftrl_model_unit& muBias, vector<ftrl_model_unit*>& theta, int f)
{double result = 0;result += muBias.u[f];for(int i = 0; i < x.size(); ++i){result += theta[i]->u[f] * x[i].second;}return result;
}double ftrl_model::get_wTx(const vector<pair<string, double> >& x, ftrl_model_unit& muBias, vector<ftrl_model_unit*>& theta, int f)
{double result = 0;result += muBias.w[f];for(int i = 0; i < x.size(); ++i){result += theta[i]->w[f] * x[i].second;}return result;
}double ftrl_model::get_uTx(const vector<pair<string, double> >& x, ftrl_model_unit& muBias, unordered_map<string, ftrl_model_unit*>& theta, int f)
{double result = 0;result += muBias.u[f];for(int i = 0; i < x.size(); ++i){result += get_uif(theta, x[i].first, f) * x[i].second;}return result;
}double ftrl_model::get_wTx(const vector<pair<string, double> >& x, ftrl_model_unit& muBias, unordered_map<string, ftrl_model_unit*>& theta, int f)
{double result = 0;result += muBias.w[f];for(int i = 0; i < x.size(); ++i){result += get_wif(theta, x[i].first, f) * x[i].second;}return result;
}**// 计算得分**
double ftrl_model::getScore(const vector<pair<string, double> >& x, ftrl_model_unit& muBias, unordered_map<string, ftrl_model_unit*>& theta)
{double result = 0;vector<double> uTx(piece_num);double max_uTx = numeric_limits<double>::lowest();for(int f = 0; f < piece_num; ++f){uTx[f] = get_uTx(x, muBias, theta, f);if(uTx[f] > max_uTx) max_uTx = uTx[f];}double numerator = 0.0;double denominator = 0.0;for(int f = 0; f < piece_num; ++f){uTx[f] -= max_uTx;uTx[f] = exp(uTx[f]);double wTx = get_wTx(x, muBias, theta, f);double s_wx = utils::sigmoid(wTx);numerator += uTx[f] * s_wx;denominator += uTx[f];}return numerator / denominator;
}double ftrl_model::get_uif(unordered_map<string, ftrl_model_unit*>& theta, const string& index, int f)
{unordered_map<string, ftrl_model_unit*>::iterator iter = theta.find(index);if(iter == theta.end()){return 0.0;}else{return iter->second->u[f];}
}double ftrl_model::get_wif(unordered_map<string, ftrl_model_unit*>& theta, const string& index, int f)
{unordered_map<string, ftrl_model_unit*>::iterator iter = theta.find(index);if(iter == theta.end()){return 0.0;}else{return iter->second->w[f];}
}void ftrl_model::outputModel(ofstream& out)
{out << "bias " << *muBias << endl;for(unordered_map<string, ftrl_model_unit*>::iterator iter = muMap.begin(); iter != muMap.end(); ++iter){out << iter->first << " " << *(iter->second) << endl;}
}void ftrl_model::debugPrintModel()
{cout << "bias " << *muBias << endl;for(unordered_map<string, ftrl_model_unit*>::iterator iter = muMap.begin(); iter != muMap.end(); ++iter){cout << iter->first << " " << *(iter->second) << endl;}
}bool ftrl_model::loadModel(ifstream& in)
{string line;if(!getline(in, line)){return false;}vector<string> strVec;utils::splitString(line, ' ', &strVec);if(strVec.size() != 6 * piece_num + 1){return false;}muBias = new ftrl_model_unit(piece_num, strVec);while(getline(in, line)){strVec.clear();utils::splitString(line, ' ', &strVec);if(strVec.size() != 6 * piece_num + 1){return false;}string& index = strVec[0];ftrl_model_unit* pMU = new ftrl_model_unit(piece_num, strVec);muMap[index] = pMU;}return true;
}
#endif /*FTRL_MODEL_H_*/

仔细阅读getScore发现predict 很简单，就是实现了一下mlr 的公式：
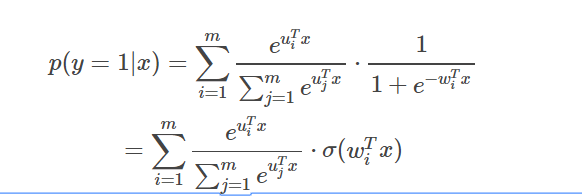
在这里插入图片描述
从公式可以看出，数据predict 时仅使用uf, wf 权重，实例截图如下：

根据以上分析，得出过滤条件uf, wf 均不为零是特征为有效特征。因此模型瘦身实现如下：

# -*- coding: utf-8 -*-
# load model and predict mlr
from __future__ import unicode_literals
#!/usr/bin/python
import sys
piece_num = int(sys.argv[3])
lite_model = open(sys.argv[2], 'w')
line_count = 0
for line in open(sys.argv[1], 'r'):if not line:breakelse:if piece_num == 1:if line.split('\t')[2] != '0':lite_model.write(line)else :line_sp = line.split()filter = Truefeature = line_sp[0]for i in xrange(piece_num):if line_sp[1+i] != '0' or line_sp[1+piece_num+i] != '0':lite_model.write(feature+"\t"+str(i)+"\t"+line_sp[1+i]+"\t"+line_sp[1+piece_num+i]+"\n")line_count+=1if line_count % 1000000 == 0:print "finishede line count:%d"%line_count# break
lite_model.close()

测试预测文件（即实现加载lite model，的predict）：

# -*- coding: utf-8 -*-
# load model and predict mlr
from __future__ import unicode_literals
#!/usr/bin/python
import sys
reload(sys)
sys.setdefaultencoding('utf-8')
import numpy as np
import math
print len(sys.argv)
if len(sys.argv)< 3:print "please input full model file name and save result file name at least!!!"exit(0)piece_num = 12
if len(sys.argv) == 4:piece_num = int(sys.argv[3])
result = open(sys.argv[2], 'w')
line_count = 0
model = {}
for line in open(sys.argv[1], 'r'):if not line:breakelse:line_sp = line.split()feature = line_sp[0]index = int(line_sp[1])u_v = float(line_sp[2])w_v = float(line_sp[3])if feature in model:model[feature][index] = [u_v, w_v]else:model[feature] = {}model[feature][index] = [u_v, w_v]line_count+=1if line_count % 1000000 == 0:print "finished line count:%d"%line_count# breakdef sigmode(x):return 1 / (1 + np.exp(-x))def get_uw_T_x(features, model):u_T_x = np.zeros(piece_num)w_T_x = np.zeros(piece_num)features.append("bias")for feature in features:u_zeros = np.zeros(piece_num)w_zeros = np.zeros(piece_num)if feature in model:for v in model[feature]:u_zeros[v] = model[feature][v][0]w_zeros[v] = model[feature][v][1]# print u_zerosu_T_x += u_zerosw_T_x += w_zerosprint u_T_xprint w_T_xu_T_x = u_T_x - np.max(u_T_x)return np.exp(u_T_x), sigmode(w_T_x)def predict(features, model):features_cal = [feature.split(":")[0] for feature in features]uTx, wTx = get_uw_T_x(features_cal, model)dim = 0.0re = 0.0for x, y in zip(uTx, wTx):re += x*ydim += xreturn re/dimfor line in sys.stdin:if not line:breakelse:# print modelline_sp = line.split("\t")line_news = "\t".join(line_sp[1:-1])label = line_sp[0]feature_line = line_sp[-1]# print feature_linefeatures = feature_line.split()# print features# breakscore = predict(features, model)print label+"\t"+str(score)+"\t"+line_newsresult.write(label+"\t"+str(score)+"\t"+line_news)break

满篇code实在难受，如若不想关心如何实现，直接使用，请关注git:
https://github.com/liguoyu1/alphaPLM/tree/master/src/scripts


http://chatgpt.dhexx.cn/article/PdWHAFNH.shtml

相关文章

推荐系统与深度学习（十五）——LS-PLM（MLR）模型原理

推荐系统与深度学习（十五）——LS-PLM（MLR）模型原理

公众号后台回复“图书“&#xff0c;了解更多号主新书内容 作者&#xff1a;livan 来源&#xff1a;数据Python与算法 模型原理 CTR预估的发展过程中&#xff0c;LR模型是比较常用的方法&#xff0c;因为其计算量小容易并行&#xff0c;工业上应用非常广泛&#xff0c;同时也引…
阅读更多...
基于R语言中的mlr以及Python中的sklearn的逻辑回归算法实战

基于R语言中的mlr以及Python中的sklearn的逻辑回归算法实战

逻辑回归算法在Python和R语言中的实现 基于R语言中的mlr、tidyverse进行逻辑回归算法实战逻辑回归是什么&#xff1f; 建立一个逻辑回归模型特征工程与特征选择数据可视化 对缺失值进行处理输出混淆矩阵 准确率、查准率、召回率、f1值、fpr、fnr上述逻辑回归模型总结&#xff1…
阅读更多...
多元线性回归MLR多变量预测模型，多变量输入结构，可以拟合出方程，评价指标包括:R2、MAE、MSE、RMSE等，代码质量极高，方便学习和替换数据。

多元线性回归MLR多变量预测模型，多变量输入结构，可以拟合出方程，评价指标包括:R2、MAE、MSE、RMSE等，代码质量极高，方便学习和替换数据。

%% 清空环境变量 warning off % 关闭报警信息 close all % 关闭开启的图窗 clear % 清空变量 clc % 清空命令行 %% %% 导入数据 resxlsread(数据集.xlsx); %% 数据分析 num_size 0.7; …
阅读更多...
深度学习与推荐系统（十五）——LS-PLM（MLR）模型

深度学习与推荐系统（十五）——LS-PLM（MLR）模型

CTR预估的发展过程中&#xff0c;LR模型是比较常用的方法&#xff0c;因为其计算量小容易并行&#xff0c;工业上应用非常广泛&#xff0c;同时也引发了各位大佬基于LR模型的优化改进&#xff0c;这一改进通常有两个方向&#xff0c;一个是走融合路&#xff0c;即GBDTLR样式&am…
阅读更多...
MLIR (Multi-Level Intermediate Representation)

MLIR (Multi-Level Intermediate Representation)

MLIR 意思为&#xff1a;多级中间表示&#xff0c;是一种新的IR表示。MLIR 是 LLVM 项目的子项目。 MLIR 是一种新型的编译器框架&#xff0c;其设计中参考了已有的编译器优点&#xff0c;规避了一些缺陷。包括了中间表示的定义、转换以及优化等功能&#xff0c;极大地方便了新…
阅读更多...
回归算法总结——SLR、MLR、PCR、PLS

回归算法总结——SLR、MLR、PCR、PLS

PCR参考链接&#xff1a;【建模应用】PCA主成分分析原理详解 - pigcv - 博客园 PLS参考链接&#xff1a;【建模应用】PLS偏最小二乘回归原理与应用 - pigcv - 博客园
阅读更多...
PCA-APCA-MLR

PCA-APCA-MLR

全称 principal component analysis-absolute principal component score-multiple linear regression 原理 绝对因子分析/多元线性回归受体模型（APCS—MLR）的基本原理是将因子分析的主因子得分转化为绝对主因子得分（APCS），各指标含量再分别对所有的APCS进行多元线性回…
阅读更多...
回归预测 | MATLAB实现MLR多元线性回归预测（多指标评价）

回归预测 | MATLAB实现MLR多元线性回归预测（多指标评价）

回归预测 | MATLAB实现MLR多元线性回归预测（多指标评价） 目录 回归预测 | MATLAB实现MLR多元线性回归预测（多指标评价）预测效果基本介绍模型描述程序设计参考资料预测效果 基本介绍 回归预测 | MATLAB实现MLR多元线性回归预测（多指标评价） 模型描述 多元线性回归（Multip…
阅读更多...
【ML】机器学习模型之PMML--概述

【ML】机器学习模型之PMML--概述

机器学习模型的应用一般会经历两个主要过程&#xff1a; 1、离线开发2、线上部署 离线部分负责模型训练和导出模型&#xff0c;线上部分负责导入模型并且做预测。 以上图片来自&#xff1a;https://zhuanlan.zhihu.com/p/30378213 一、PMML简要介绍 PMML&#xff08;Predic…
阅读更多...
基于 mlr 包的逻辑回归算法介绍与实践

基于 mlr 包的逻辑回归算法介绍与实践

逻辑回归是基于概率分类的有监督学习算法，它依赖于直线方程，产生的模型非常容易解释和交流。在其最简单的形式中，逻辑回归被用来预测二分类问题，但算法的变体也可以处理多个类。 逻辑回归算法通常应用于二分类问题，称为二项逻辑回归 (binomial logistic regression)，当处…
阅读更多...
利用R语言中的tidyverse和mlr建立分类算法-KNN

利用R语言中的tidyverse和mlr建立分类算法-KNN

基于相似性的k近邻分类 KNN&#xff08;K-Nearest Neighbors&#xff09;算法是一种基本的分类和回归算法&#xff0c;它是一种非参数算法&#xff0c;可以用于分类和回归问题。它的基本思想是利用已有的数据集对新的数据进行分类或回归。 在分类问题中&#xff0c;KNN算法通…
阅读更多...
MLR原理及deepctr组网实现MLR

MLR原理及deepctr组网实现MLR

文章目录 MLRdeepctr实现MLR MLR https://zhuanlan.zhihu.com/p/100532677 https://blog.csdn.net/fyneru_xiaohui/article/details/106390266 deepctr实现MLR import os, warnings, time, sys import pickle import matplotlib.pyplot as plt import pandas as pd, numpy a…
阅读更多...
R手册(Machine Learning)--mlr (Part 2)

R手册(Machine Learning)--mlr (Part 2)

文章目录 Configuration (配置)Parallelization (并行)Imputation (插补)Feature Extraction (特征提取)1. Feature filtering(特征筛选)2. Feature selection(特征选择) Benchmarking (基准点)Visualization (可视化)Wrappers (封装器)Nested Resampling (嵌套重采样)Ensemble…
阅读更多...
R手册(Machine Learning)--mlr(Part 1)

R手册(Machine Learning)--mlr(Part 1)

文章目录 IntroductionPreprocessing data (预处理)Task and Learner1. Create a task2. Making a learner Training & Testing (训练和测试)1. Setting hyperparameters (设置超参数)2. Train a model and predict (训练模型和预测)3. Measuring performance (模型评估质量…
阅读更多...
基于EEMD+GRU+MLR的时间序列预测

基于EEMD+GRU+MLR的时间序列预测

0、前言 文章《基于 EEMD-GRU-MLR 的短期电力负荷预测》中&#xff0c;通过构建集合经验模态分解(ensemble empirical modedecomposition&#xff0c;EEMD)以及门控循环单元神经网络(gated recurrent unit neural network&#xff0c;GRU)和多元线性回归(multiplelinear regres…
阅读更多...
机器学习的R实现（mlr包）

机器学习的R实现（mlr包）

目录 Machine Learning with MLR Package 1. 获取数据 2. 探索数据 3. 缺失值填补 4. 特征工程 5. 机器学习 1. 二次判别分析&#xff0c;Quadratic Discriminant Analysis (QDA). 2.逻辑回归 Logistic Regression 3. 决策树-Decision Tree 4. 随机森林&#xff0c;Ra…
阅读更多...
机器学习之MLR

机器学习之MLR

线性回归&#xff08;Linear regression&#xff09;是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为一元回归&#xff0c;大于一个自变量情…
阅读更多...
MLR（mixed logistic regression）模型

MLR（mixed logistic regression）模型

基本形式 MLR模型是阿里巴巴12年提出&#xff08;17年发表&#xff09;点击率预估模型&#xff0c;它利用分段方式对数据进行拟合&#xff0c;相比LR模型&#xff0c;能够学习到更高阶的特征组合。其基本表达式如下 p ( y 1 ∣ x ) g ( ∑ j 1 m σ ( u j T x ) η ( w j …
阅读更多...
MLR（mixed logistic regression）算法原理及实现

MLR（mixed logistic regression）算法原理及实现

MLR&#xff08;mixed logistic regression&#xff09;算法 参考https://zhuanlan.zhihu.com/p/77798409?utm_sourcewechat_session 盖坤ppt : https://wenku.baidu.com/view/b0e8976f2b160b4e767fcfdc.html 原文&#xff1a;《Learning Piece-wise Linear Models from Large…
阅读更多...
多元线性回归MLR

多元线性回归MLR

多元线性回归(MLR) 文章目录 多元线性回归(MLR)由极大似然估计(MLE, Maximum likelihood estimation)推导MSE简单导数知识推导解析解( θ ( X T X ) − 1 X T Y \theta (X^TX)^{-1}X^TY θ(XTX)−1XTY)来个例子试一试吧 不用解析解, 用梯度下降求解 θ \theta θ梯度下降法另…
阅读更多...
推荐文章

Copyright @ 2022~2023