逻辑回归算法在Python和R语言中的实现
- 基于R语言中的mlr、tidyverse进行逻辑回归算法实战
- 逻辑回归是什么?
- 建立一个逻辑回归模型
- 特征工程与特征选择
- 数据可视化
- 对缺失值进行处理
- 输出混淆矩阵
- 准确率、查准率、召回率、f1值、fpr、fnr
- 上述逻辑回归模型总结:
- 省略变量Fare重新建模
- 对name一列进行特征提取与特征构造
- 将新构造的特征加入模型
- 对新数据进行训练以及10折交叉验证
- 输出混淆矩阵
- 下面对泰坦尼克号数据集中的测试集进行预测
- 调用训练好的模型进行预测
- 输出预测值
- 基于Python的逻辑回归分类算法实践
- 建模
- 使用10折交叉验证评估模型
- Python与R中的mlr进行对比
基于R语言中的mlr、tidyverse进行逻辑回归算法实战
逻辑回归是什么?
首先逻辑回归是一个二分类算法,线性回归于逻辑回归算法的区别在于:
前者是学习预测变量与连续结果变量之间的关系,而后者学习预测变量与分类结果变量之间的关系。
确切的说,在线性回归中,我们最后要拟合的曲线为: y = w x + b y= wx+b y=wx+b,而在逻辑回归中,我们需要拟合的是 y = 1 1 + e − ( w x + b ) y= \dfrac{1}{1+e^{-(wx+b)}} y=1+e−(wx+b)1,后者的函数又称[sigmoid函数]{.underline},而sigmoid函数又是神经网络中很重要的激活函数,所有逻辑回归算法在联系机器学习算法和深度学习算法中具有重要的作用。
在逻辑回归算法中涉及到的统计学知识为最大似然估计,即根据样本结果去估计统计学参数 w , b w,b w,b,依据独立性假设条件,假设样本被预测为正例的概率为 p = 1 1 + e − ( w x + b ) p=\dfrac{1}{1+e^{-(wx+b)}} p=1+e−(wx+b)1,则样本被预测为反例的概率为: 1 − p 1-p 1−p,我们将上面两个部分简化一下得到: p ( y i ∣ x i , w , b ) = p y i ( 1 − p ) 1 − y i p(y_i|x_i,w,b)=p^{y_i}(1-p)^{1-y_i} p(yi∣xi,w,b)=pyi(1−p)1−yi
当 y i = 1 y_i=1 yi=1时, p ( y i ∣ x i , w , b ) = p p(y_i|x_i,w,b)=p p(yi∣xi,w,b)=p,否则, p ( y i ∣ x i , w , b ) = 1 − p p(y_i|x_i,w,b)=1-p p(yi∣xi,w,b)=1−p,假设我们有 n n n个样本,根据极大似然估计的原理,为了估计参数 w , b w,b w,b,我们需要极大化下面的函数: ∏ i = 1 n p y i ( 1 − p ) 1 − y i \prod_{i=1}^np^{y_i}(1-p)^{1-y_i} i=1∏npyi(1−p)1−yi
通常在处理极大似然估计时,为了计算方便,我们需要将上面的公示取对数,这是因为对数函数是单调的,且取了对数之后,连乘变为连加,会降低计算难度,即 max w , b ∑ i = 1 n [ y i l o g p + ( 1 − y i ) l o g ( 1 − p ) ] \max_{w,b}\sum_{i=1}^n [y_ilog p+(1-y_i)log(1-p)] w,bmaxi=1∑n[yilogp+(1−yi)log(1−p)]
将 p = 1 1 + e − ( w x + b ) p=\dfrac{1}{1+e^{-(wx+b)}} p=1+e−(wx+b)1带入上式最终得到: max w , b ∑ i = 1 n { y i l o g ( 1 1 + e − ( w x i + b ) ) + ( 1 − y i ) l o g ( 1 − 1 1 + e − ( w x i + b ) ) } \max_{w,b}\sum_{i=1}^n \{y_ilog(\dfrac{1}{1+e^{-(wx_i+b)}})+(1-y_i)log(1-\dfrac{1}{1+e^{-(wx_i+b)}})\} w,bmaxi=1∑n{yilog(1+e−(wxi+b)1)+(1−yi)log(1−1+e−(wxi+b)1)},i.e. max w , b ∑ i = 1 n { y i ( w x i + b ) − l o g ( 1 + e w x i + b ) } \max_{w,b}\sum_{i=1}^n \{y_i(wx_i+b)-log(1+e^{wx_i+b})\} w,bmaxi=1∑n{yi(wxi+b)−log(1+ewxi+b)}
i.e. min w , b f ( w , b ) = min w , b ∑ i = 1 n { l o g ( 1 + e w x i + b ) − y i ( w x i + b ) } \min_{w,b} f(w,b)=\min_{w,b}\sum_{i=1}^n \{log(1+e^{wx_i+b})-y_i(wx_i+b)\} w,bminf(w,b)=w,bmini=1∑n{log(1+ewxi+b)−yi(wxi+b)}
可验证 f ( w , b ) f(w,b) f(w,b) 是一个凸函数:定义域为整个欧式空间,且 f ′ ′ ( w , b ) = f ′ ′ ( β ) = ∑ i = 1 n x i x i T e β x i ( 1 + e β x ) 2 ≥ 0 f^{''}(w,b)=f^{''}(\beta)=\sum_{i=1}^n\dfrac{x_ix_i^Te^{\beta x_i}}{(1+e^{\beta x})^2}\geq0 f′′(w,b)=f′′(β)=∑i=1n(1+eβx)2xixiTeβxi≥0
因此,由凸优化理论知:该函数是一个凸函数,且存在全局的最优解 w , b w,b w,b;对于参数寻优的建模问题,我们一般选择梯度下降算法进行迭代,包括:批量梯度下降(GD)、随机梯度下降(SGD)、小批量梯度下降(batchsize GD)。
我们以梯度下降算法为例,首先求解 ∇ β f ( β ) = ∑ i = 1 n { 1 1 + e − β T x i − y i x i } = ∑ i = 1 n { s i g m o i d ( β T x i ) − y i x i } \nabla_{\beta} f(\beta)=\sum_{i=1}^n\{\dfrac{1}{1+e^-{\beta^Tx_i}}-y_ix_i\}=\sum_{i=1}^n\{sigmoid(\beta^Tx_i)-y_ix_i\} ∇βf(β)=∑i=1n{1+e−βTxi1−yixi}=∑i=1n{sigmoid(βTxi)−yixi}
因此在每次迭代时,参数 β \beta β的更新方式为:
β i + 1 = β i − l . ∇ β f ( β ) = β i − l . ∑ i = 1 n { 1 1 + e − β T x i − y i x i } \beta_{i+1}=\beta_i-l.\nabla_\beta f(\beta)=\beta_i-l.\sum_{i=1}^n\{\dfrac{1}{1+e^-{\beta^Tx_i}}-y_ix_i\} βi+1=βi−l.∇βf(β)=βi−l.i=1∑n{1+e−βTxi1−yixi}
其中 l l l为学习速率,一般为0.001、0.01等小数
建立一个逻辑回归模型
library(mlr)
library(tidyverse)
#install.packages("titanic") #加载
data(titanic_train,package = "titanic") #加载泰坦尼克号的数据集
tatanicTib <- as_tibble(titanic_train)
tatanicTib
特征工程与特征选择
在对泰坦尼克号数据集进行特征工程和特征选择之前,有必要了解一下什么是特征工程、特征选择。
特征工程是指通过对数据进行处理和转换,构建出更加有用、有代表性的特征,以提高模型的预测性能。通常情况下,原始数据中包含的特征可能过于复杂或者过于冗余,需要进行一系列的处理,包括特征选择、特征提取、特征变换、特征创造等等。
特征选择是指从原始特征中挑选出最具有代表性、最相关的特征,并剔除无用或冗余的特征。特征选择可以提高模型的泛化能力和鲁棒性,减少过拟合的风险,同时也可以降低计算成本和存储空间的开销。
-
特征工程:
- 特征提取:从原始数据中提取出有用的信息,比如文本数据的词频、TF-IDF特征、图像数据的颜色、纹理和形状等。
- 特征变换:通过一系列的变换,将原始特征转换成更具有代表性的新特征,比如主成分分析(PCA)、线性判别分析(LDA)、核变换(Kernel Trick)等。
- 特征创造:通过对原始特征进行组合、衍生或者交叉,构建出新的特征,以增强模型的表达能力。
-
特征选择:
- 过滤式特征选择:通过统计学方法或者相关系数,选择与目标变量最相关的特征。
- 包裹式特征选择:将特征选择看作是一个搜索问题,从特征子集中选择最优的子集,以最小化目标函数。
- 嵌入式特征选择:将特征选择嵌入到模型训练的过程中,比如正则化方法,以减少过拟合的风险
过滤式特征选择、包裹式特征选择、嵌入式特征选择都是特征选择的常用方法。
- 过滤式特征选择:
过滤式特征选择是通过对每个特征与目标变量之间的相关性进行评估,来选择最相关的特征。常用的方法包括:
- 方差选择:选择方差较大的特征,可以用于去除低方差特征。
- 互信息选择:选择与目标变量相关性较高的特征,可以用于处理离散变量。
- 卡方检验:选择与目标变量显著相关的特征,可以用于处理分类问题。
- 相关系数:选择与目标变量相关性较高的特征,可以用于处理连续变量。
- 包裹式特征选择:
包裹式特征选择是将特征选择看作是一个搜索问题,从特征子集中选择最优的子集,以最小化目标函数。常用的方法包括:
- 递归特征消除(RFE):通过反复训练模型,每次去掉最不重要的特征,来选择最优的特征子集。
- 遗传算法:模拟生物进化过程,通过交叉、变异、选择等操作来不断优化特征子集。
- 基于模型的优化:通过训练一个模型,将预测误差作为目标函数,从而选择最优的特征子集。
- 嵌入式特征选择:
嵌入式特征选择是将特征选择嵌入到模型训练的过程中,通过正则化等方法来减少过拟合的风险。常用的方法包括:
- L1正则化(Lasso):通过L1正则化,将一些不重要的特征的系数缩小到零,从而实现特征选择。
- L2正则化(Ridge):通过L2正则化,将特征系数限制在一个较小的范围内,从而减少过拟合的风险。
- 弹性网络(Elastic Net):综合L1和L2正则化的优点,可以同时实现特征选择和过拟合控制。
总之,不同的特征选择方法适用于不同的问题和数据集,需要根据具体情况进行选择和应用。
tatanicTib <- tatanicTib[tatanicTib$Embarked!="",]#删除Embarked所在列值为空的行
colSums(is.na(tatanicTib))
facts <- c("Survived","Sex","Pclass","Embarked") #这四个变量是类别变量
titanic_Clean <- tatanicTib %>%mutate_at(.vars = facts,.funs = factor) %>% #将facts变量转化为类别变量 factormutate(FamSize = SibSp+Parch) %>% #构建新的特征为家庭总人数select(Survived,Pclass,Sex,Age,Fare,FamSize,Embarked) #选择以上七个特征进行预测
数据可视化
titanicUntidy <- gather(titanic_Clean,key = "Variable",value = "Value",-Survived) # 该函数就是将所有的自变量的名称都放在一列,-Survived表示除了Survived这一列以外都进行这个操作
# 为每个连续变量创建子图
titanicUntidy %>%filter(Variable != "Pclass"&Variable !="Sex" & Variable !="Embarked" )%>% #首先过滤掉类别变量ggplot(aes(x=Survived,y=as.numeric(Value)))+facet_wrap(~ Variable,scales = "free_y")+#按照Variable变量进行分组,free_y代表纵轴刻度可以自动调整geom_violin(draw_quantiles = c(0.25,0.5,0.75))+# 小提琴图形显示了数据沿着y轴的密度分布,三个线条分别代表第一四分位数、中位数、第三四分位数geom_point(alpha=0.05,size=3)+theme_bw()
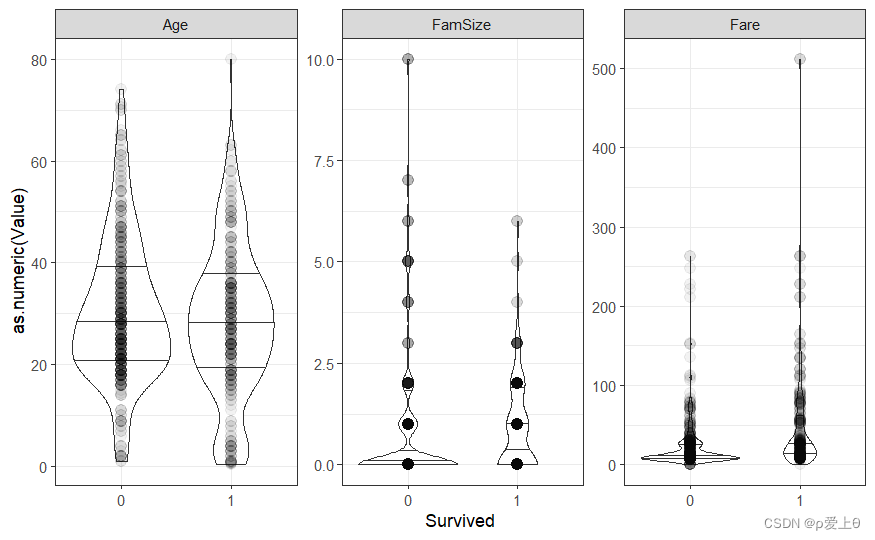
# 为每个分类变量创建子图
titanicUntidy %>%filter(Variable=="Pclass"| Variable=="Sex" | Variable=="Embarked")%>%ggplot(aes(x=Value,fill=Survived))+ #fill表示填充颜色变量,生成一个堆积柱状图facet_wrap(~ Variable,scales = "free_x")+geom_bar(position = "stack")+theme_bw()
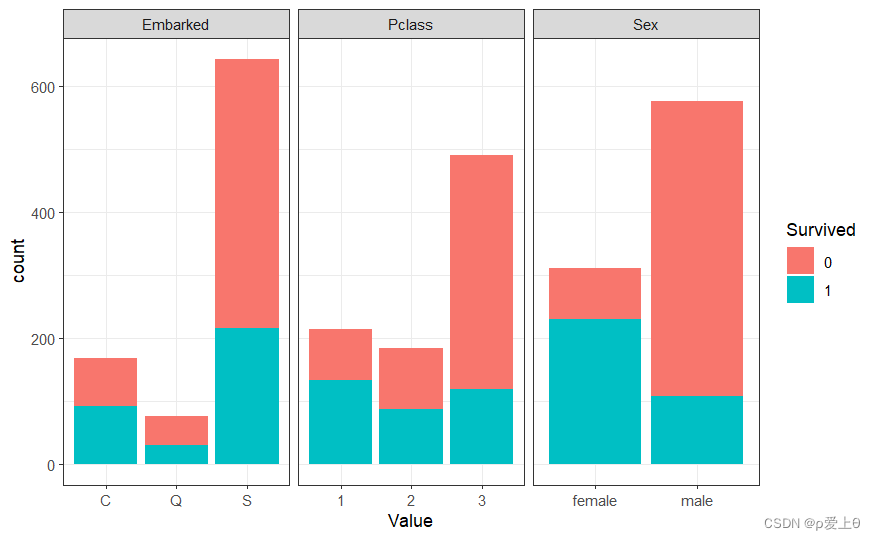
对缺失值进行处理
# 首先检查titanic_Clean 数据框有哪几列含有缺失值
colSums(is.na(titanic_Clean)) # 显示Age列有177个缺失值
# 现在对缺失值进行补充
imp <- impute(titanic_Clean,cols = list(Age=imputeMean()))#对缺失值填充平均值# 对缺失值处理后的数据进行ML建模,使用逻辑回归算法
TitanicTask <-makeClassifTask(data = imp$data,target = "Survived")#定义分类任务
LogReg <- makeLearner("classif.logreg",predict.type = "prob")#定义学习器# 使用交叉验证进行模型的训练与评估
LogRegwrapper <- makeImputeWrapper("classif.logreg",cols = list(Age = imputeMean())) #对学习器和插补方法进行封装
kFold <- makeResampleDesc(method="RepCV",folds = 10,reps = 50,stratify = TRUE) #十折交叉验证,并且重复50次,采用分层抽样法
LogwithImpute <- resample(learner = LogRegwrapper,task = TitanicTask,resampling = kFold,measures = list(acc,fpr,fnr))输出混淆矩阵
calculateConfusionMatrix(LogwithImpute$pred,relative = TRUE)
准确率、查准率、召回率、f1值、fpr、fnr
- 精确率(Precision) 精确率是指分类模型预测为正例的样本中,实际为正例的比例。精确率越高,表示模型预测的结果中真正为正例的比例越高,模型的误判率越低。但是,当样本中正例的比例较低时,精确率可能会高,但模型的实际预测效果并不好。
- 准确率(Accuracy) 准确率是指分类模型预测正确的样本数量占总样本数量的比例。准确率越高,表示模型预测的结果中正确的比例越高,模型的整体效果越好。但是,当样本中正例的比例较低时,准确率可能会高,但模型的实际预测效果并不好。
- 召回率(Recall) 召回率是指分类模型正确预测为正例的样本数量占实际为正例的样本数量的比例。
- FPR(False Positive Rate) FPR是指分类模型将负例错误预测为正例的比例,即实际为负例的样本中,被模型错误预测为正例的比例.
- FNR(False Negative Rate) FNR是指分类模型将正例错误预测为负例的比例,即实际为正例的样本中,被模型错误预测为负例的比例。
上述逻辑回归模型总结:
尽管我们的模型在整体的准确率(accuracy)为80%,但是该模型将百分之三十的死亡乘客预测成了幸存乘客;而将百分之十三的幸存乘客预测成了死亡乘客。由此可知,我们上面的模型并没有将数据集中的有效信息完全挖掘出来,因此,准确率并不是最重要的性能度量指标,尤其是在因变量分布不均衡时。
由于模型最后预测的是对数几率: ln p 1 − p = β 0 + β 1 x 1 + β 2 x 2 + ⋯ + β k x k \ln \dfrac{p}{1-p}=\beta_0+\beta_1x_1+\beta_2x_2+\cdots+\beta_kx_k ln1−pp=β0+β1x1+β2x2+⋯+βkxk,其中 p p p代表预测为正例的概率,在本案例中: p p p代表逻辑回归模型预测乘客为幸存者的概率,预测变量有 x 1 = P c l a s s , x 2 = S e x , x 3 = A g e , x 4 = F a r e , x 5 = F a m S i z e , x 6 = E m b a r k e d x_1 = Pclass,x_2= Sex,x_3 = Age,x_4 = Fare,x_5 = FamSize,x_6 = Embarked x1=Pclass,x2=Sex,x3=Age,x4=Fare,x5=FamSize,x6=Embarked,我们可以coef()函数将每个自变量前的系数打印出来:
LogModel <- train(LogReg,task = TitanicTask)
logRegModelData <- getLearnerModel(LogModel)
coef(logRegModelData)
下面我们将对数几率 ln p 1 − p \ln \dfrac{p}{1-p} ln1−pp转换为几率比 p 1 − p \dfrac{p}{1-p} 1−pp,由关系式可以知道,将对数几率比取个指数即可:
exp(cbind(Odds_Ratio = coef(logRegModelData),confint(logRegModelData)))
# confint()函数可以计算95%的置信区间,可以帮助确定每个变量的预测值的可信度有多大
对于分类变量:我们以Sexmale为例,该变量的几率比为0.06,即 p m a l e 1 − p m a l e = 0.06 \dfrac{p_{male}}{1-p_{male}}=0.06 1−pmalepmale=0.06,也就是说男性的存活概率相对于女性是0.06,更通俗的讲:女性的存活概率是男性的 1 0.06 = 16.7 \frac{1}{0.06}=16.7 0.061=16.7倍
对于连续变量,可以将几率比解释为:变量每增加一个单位,乘客幸存的可能性就会增加多少。以FamSize为例:在取指数之前,Famsize对于对数几率比的参数值是负数,说明,家庭总人口数量每增加一人,存活的概率就会减少20%
95%的置信区间表示每个变量的预测值的可信度。几率比为1表示几率相等,变量对预测没有影响,因此如果置信区间包括值1,就说明该变量在模型的预测中不起什么作用,例如变量Fare
省略变量Fare重新建模
titanicNoFare <- select(titanic_Clean,-Fare)
titanincNoFareTask <- makeClassifTask(data = titanicNoFare,target = "Survived")
LogRegNoFare <- resample(learner = LogRegwrapper,task = titanincNoFareTask,resampling = kFold,measures = list(acc,fpr,fnr))
去掉Fare变量发现相关的度量性能都小幅度下降,但差异不大,这也进一步证实了上面的参数分析过程。
对name一列进行特征提取与特征构造
# 首先要从name变量中提取问候语 Mr、Mrs、Dr、Master、Miss、Rev,将不是以上称谓的赋值为other
surnames <- map_chr(str_split(tatanicTib$Name,"\\."),1)#对每个姓名以.进行分割,并取分割后的第一个元素salutations <- map_chr(str_split(surnames,", "),2)#对第一步分割的字符再以", "分割,最后取第二个元素salutations[!(salutations %in% c("Mr","Mrs","Dr","Master","Miss","Rev"))]<- "other"
将新构造的特征加入模型
factsWithSal <- c("Survived","Sex","Pclass","Embarked","Salutations") #这五个变量是类别变量
titanicWithSal <- tatanicTib %>%mutate(FamSize = SibSp+Parch,Salutations = salutations) %>% #构建新的特征为家庭总人数以及名称mutate_at(.vars = factsWithSal,.funs = factor) %>% #将facts变量转化为类别变量 factorselect(Survived,Pclass,Sex,Age,Fare,FamSize,Embarked,Salutations) #选择以上八个特征进行预测
titanicUntidySal <- gather(titanicWithSal,key = "Variable",value = "Value",-Survived) # 该函数就是将所有的自变量的名称都放在一列,-Survived表示除了Survived这一列以外都进行这个操作
# 为每个分类变量创建子图
titanicUntidySal %>%filter(Variable=="Pclass"| Variable=="Sex" | Variable=="Embarked"|Variable =="Salutations")%>%ggplot(aes(x=Value,fill=Survived))+ #fill表示填充颜色变量,生成一个堆积柱状图facet_wrap(~ Variable,scales = "free_x")+geom_bar(position = "stack")+theme_bw()
对新数据进行训练以及10折交叉验证
# 模型的训练
newtask <- makeClassifTask(data = titanicWithSal,target = "Survived") #定义新的分类任务
newLogWrapper <- makeImputeWrapper("classif.logreg",cols= list(Age=imputeMean())) #定义新的学习器,使用makeImputeWrapper函数对逻辑回归学习器以及缺失值处理方法进行封装
newLogModel <- train(learner = newLogWrapper,task = newtask)
# 10折交叉验证-对模型进行评估
KFold <- makeResampleDesc(method = "RepCV",folds=10,reps=50,stratify = TRUE)
LogWithSal <- resample(learner = newLogWrapper,task = newtask,resampling = KFold,measures = list(acc,fpr,fnr))
输出混淆矩阵
calculateConfusionMatrix(LogWithSal$pred,relative = TRUE)
总结:增加了新的特征Salutations后发现:无论是accuracy还是fnr、fpr都有了显著改进,也就是说该列特征有益于改进模型的性能。
下面对泰坦尼克号数据集中的测试集进行预测
data(titanic_test,package = "titanic")
titanicNew <- as_tibble(titanic_test)
titanicNew <- titanicNew[titanicNew$Embarked!="",]
testsurnames <- map_chr(str_split(titanicNew$Name,"\\."),1)
testSalutations <- map_chr(str_split(testsurnames,", "),2)testSalutations[!(testSalutations %in% c("Mr","Mrs","Dr","Master","Miss","Rev"))]<- "other"
factsSal <- c("Sex","Pclass","Embarked","Salutations")
titanicNew_Clean <- titanicNew %>%mutate(FamSize=SibSp+Parch,Salutations=testSalutations)%>%mutate_at(.vars = factsSal,.funs = factor)%>%select(Pclass,Sex,Age,Fare,FamSize,Embarked,Salutations)
调用训练好的模型进行预测
y_pre<-predict(newLogModel,newdata= titanicNew_Clean)
输出预测值
getPredictionResponse(y_pre)
注意:在机器学习算法中,train过程和K-折交叉验证大部分是同时进行的。train过程是指使用一个训练集(training-set)来拟合模型,从而得到一个可以用于预测的模型。在train过程中,通常会使用特定的算法和模型参数对训练集进行训练,得到一个最优的模型。
k-折交叉验证是一种模型评估方法,它将数据集分成k个子集,每次选取其中的一个子集作为验证集,剩下的k-1个子集作为训练集,进行k次训练和验证,从而得到一个可靠的模型评估结果。k-折交叉验证可以帮助我们评估模型的泛化能力,即模型对新数据的预测能力。
需要注意的是,k-折交叉验证不同于train过程,它只是用于模型评估的一种方法。在实际应用中,train过程和k-折交叉验证通常会多次重复进行,以得到更加准确和可靠的结果。同时,选择合适的算法、模型参数和评估指标也是非常重要的。
下面我们使用Python中的sklearn对上面的数据进行建模。
基于Python的逻辑回归分类算法实践
为了方便,我们只对上面最后一种情形中的数据进行建模,首先我们将数据导入csv文件。
#write_csv(titanicWithSal,file = "Titanic_train.csv")
#write_csv(titanicNew_Clean,file="Titanic_test.csv")
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import f1_score,classification_report,accuracy_score,confusion_matrixtrain = pd.read_csv("Titanic_train.csv")
train.info()
# 现在对缺失值进行处理
train['Age'] = train['Age'].fillna(train["Age"].mean())
train.info()
# 将性别这一列的变量值转变为数字 0:female 1:male
sex_map ={"female":0,"male":1}
train["Sex"]=train["Sex"].map(sex_map)
#train.head(5)
# 现在对类别变量进行独热编码
df_Embarked = pd.DataFrame()
df_Embarked = pd.get_dummies(train["Embarked"],prefix="Embarked")
df_Sal = pd.DataFrame()
df_Sal = pd.get_dummies(train["Salutations"],prefix="Salu")
# 现在将独热编码之后的表格与原表格整理在一起,同时删除掉独热编码之前的列
train = pd.concat([train,df_Embarked],axis=1)
train = pd.concat([train,df_Sal],axis=1)
train.drop('Embarked',axis=1,inplace=True)
train.drop('Salutations',axis=1,inplace=True)
train.info()
建模
LogModel = LogisticRegression(max_iter=2000)
y_train = train["Survived"]
x_train = train.drop("Survived",axis=1,inplace=False)
x_train = x_train.values
y_train = y_train.values
LogModel.fit(x_train,y_train)
使用10折交叉验证评估模型
from sklearn.model_selection import KFold
k = 10
# 初始化KFold对象
kf = KFold(n_splits=k, shuffle=True, random_state=42)
# 定义一个空列表,用于存储每次模型评估的结果
acc = []
Fpr = []
Fnr = []
for train_index,test_index in kf.split(x_train):X_train,X_test = x_train[train_index],x_train[test_index]Y_train,Y_test = y_train[train_index],y_train[test_index]# 初始化逻辑回归模型myLogModel = LogisticRegression(max_iter=1000)# 训练myLogModel.fit(X_train,Y_train)# 预测y_pre = myLogModel.predict(X_test)cm = confusion_matrix(Y_test, y_pre)# 计算fpr和fnrtn, fp, fn, tp = cm.ravel()fpr = fp / (tn + fp)fnr = fn / (tp + fn)print(accuracy_score(y_pre,Y_test))acc.append(accuracy_score(y_pre,Y_test))Fpr.append(fpr)Fnr.append(fnr)
print(sum(acc)/k)
print(sum(Fpr)/k)
print(sum(Fnr)/k)Python与R中的mlr进行对比
| 性能度量指标 | Python | R |
|---|---|---|
| accuracy | 0.8245 | 0.8247 |
| fpr | 0.1222 | 0.26 |
| fnr | 0.2634 | 0.1227 |
: Python与R语言在性能度量的对比