文章来源：“万维钢·精英日课4——排序不等式”

“排序不等式”描述了无限制系统的“效率”和“公平”的本质关系。给我在如何分配资源上带来了很好的启发，这里记录一下大概内容，方便自已临时翻阅。

1.什么是排序不等式？

大数乘大数加上小数乘小数，大于大数乘小数加小数乘大数，这就叫排序不等式。

当有两组数字Xn和Yn，我们按从小到大分别排序如下：

 

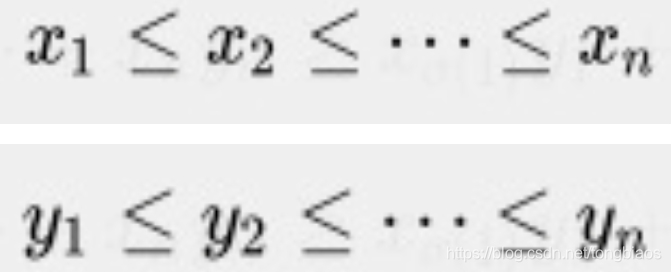
那么有如下结论：

简单说就是按照从小到大的“顺序”相乘的和最大；按照相反顺序，也就是“逆序”相乘的和最小；混乱顺序则处于二者之间。

2.资源配置的“零阶道理”

排序不等式，是资源配置的“零阶道理”。是最底层的“不平等关系”。而正是因为这个逻辑，“效率”和“公平”本质上是矛盾的。

案例1：

案例2：

所以最好的资源应该用在最赚钱的地方，最厉害的人员应该放在最关键的岗位。最好的电影应该乘以最好的导演再乘以最好的演员、然后给最多的院线排期。

这就是为什么好东西总爱扎堆，有志向的年轻人非得去大城市。这也是为什么会有马太效应，为什么人人都想跟最好的合作。这也是为什么市场总是让财富分布不平等。

3.不同系统的资源配置

常见的3种系统：不设限系统、上限系统、下限系统。

如果你是一个系统的运行者，你必须清楚判断这是一个不设限系统，还是一个有上限或者下限的系统，然后再看排序不等式是否适合该系统。

个人感觉文章中的上限系统的资源配置我没有理解得太清楚，后面有新想法再补充。

1.不设限系统（总量型）

公司在乎的是总收入，本质上是个不设限的系统、排序不等式告诉我们这样的系统应该狠抓“长板”，因为长板最能提高总量。

2.下限系统（防守型）

关注各个相加项的大小有一个下限。

①如福利系统，在贫困山区建设通讯基站效率不高，但是贫困山区需要通讯基站。福利系统解决的是公平问题。这种系统有时候会把最好的官员排到最贫困的地区去，并不指望他们创造什么效益，只是希望提高那些地区的下限。而既然是为了公平，那就必然牺牲了效率。

②安全系统也强调下限。只要是防守，我们最关心的一定是最薄弱的地方，要把最好的资源和人手放在那个地方。

3.上限系统（平均型）

很多系统对组成部分的要求是有上限的。你造一个大桥，不会重点打造其中一个桥墩，如果别的地方出问题这个桥墩再好也没用。汽车上的零件也不是越“好”越好，最理想的情况是所有难以更换的零件的磨损寿命是一样的。

<-------------------------------------------------------------------------------------->

都不记得上次在CSDN上是什么时候写东西了，感觉是比原来方便了很多啊！还是熟悉的味道！