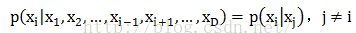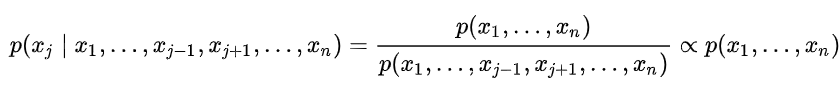Bayesian Linear Regression

考虑只有一个自变量(independent variable)的线性回归的情况，拟合数据对$(y_i,x_i),i=1,2,\dots ,N$，需要找出后验分布中的截距(intercept)${\beta }_0$和斜率/梯度(gradient)以及精度$\tau$(方差的倒数，the reciprocal of the variance)，模型可以表示为
$$y_i\sim \mathcal{N}({\beta }_0+{\beta }_1{x}_i,1/\tau )$$
或者等价的
$$y_i={\beta }_0+{\beta }_1{x}_i+\epsilon ,\epsilon \sim \mathcal{N}(0,1/\tau )$$
模型的似然函数可以被表示为$N$个i.i.d观测点的乘积
$$L(y_1,\dots ,y_N,x_1,x_2,\dots ,x_N\mid {\beta }_0,{\beta }_1,\tau )=\prod _{i=1}^N\mathcal{N}({\beta }_0+{\beta }_1{x}_i,1/\tau )$$
希望设置${\beta }_0,{\beta }_1,\tau$得到共轭先验, conjugate priors
$$\{\begin{array}{rl}& {\beta }_0\sim \mathcal{N}({\mu }_0,1/{\tau }_0)\\ & {\beta }_1\sim \mathcal{N}({\mu }_1,1/{\tau }_1)\\ & \tau \sim \Gamma (\alpha ,\beta )\end{array}$$

Gibbs Sampling

吉布斯采样的工作流程如下，假设我们有两个参数${\theta }_1$和${\theta }_2$以及一些数据$x$，目标是找到后验分布$p({\theta }_1,{\theta }_2\mid x)$.

To do this in a Gibbs sampling regime, we need to work out the conditional distributions $p({\theta }_1\mid {\theta }_1,x)$ and $p({\theta }_2\mid {\theta }_1,x)$.

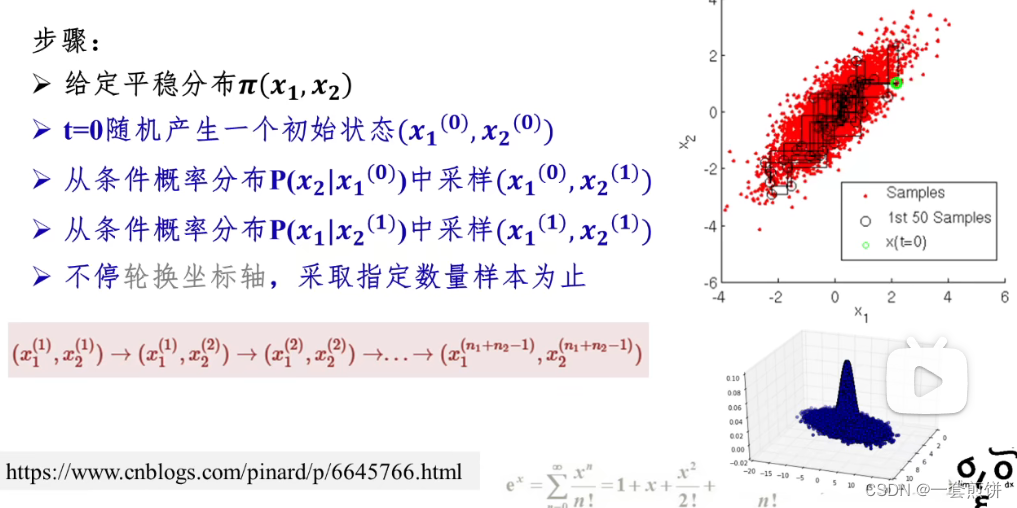
采样算法流程如下：

1. 选择初始参数${\theta }_2^{(i+1)}$
2. 采样${\theta }_1^{(i+1)}\sim p({\theta }_1\mid {\theta }_2^{(i)},x)$
3. 采样${\theta }_2^{i+1}\sim p({\theta }_2\mid {\theta }_1^{(i+1)},x)$
   流程重复$K$轮，可以采集到$K$个样本.

The key thing to remember in Gibbs sampling is to always use the most recent parameter values for all samples (e.g. sample ${\theta }_2^{(i+1)}\sim p({\theta }_2\mid {\theta }_1^{(i+1)},x)$ and not ${\theta }_2^{i+1}\sim p({\theta }_2\mid {\theta }_1^{(i)},x)$ provided ${\theta }_1^{(i+1)}$ has already been sampled).
The massive advantage of Gibbs sampling over other MCMC methods (namely Metropolis-Hastings) is that no tuning parameters are required.

Derving a Gibbs sampler

推导步骤如下

1. Write down the posterior conditional density in log-form
2. Throw away all terms that don’t depend on the current sampling variable
3. Pretend this is the density for your variable of interest and all other variables are fixed. What distribution does the log-density remind of?

Update for ${\beta }_0$

由贝叶斯公式可以得到
$$p({\beta }_0\mid {\beta }_1,\tau ,y,x)\propto p(y,x\mid {\beta }_0,{\beta }_1,\tau )p({\beta }_0)$$
其中$p(y,x\mid {\beta }_0,{\beta }_1,\tau )$是似然函数.
如果变量$x$服从期望为$\mu$，精度为$\tau$的正态分布，关于$x$的对数项（the log-dependence on x）为
$$\frac{\tau }{2}(x-\mu {)}^2\propto -\frac{\tau }{2}{x}^2+\tau \mu x$$
对数形式下关于${\beta }_0$的项为
$$-\frac{{\tau }_0}{2}({\beta }_0-{\mu }_0{)}^2-\frac{\tau }{2}\sum _{i=1}^N(y_i-{\beta }_0-{\beta }_1{x}_i{)}^2$$

Although it is perhaps not obvious, this expression is quadratic in ${\beta }_0$, meaning the conditional sampling density for ${\beta }_0$ will also be normal. A bit of algebra(dropping all terms that do not involve ${\beta }_0$) is

$$-\frac{{\tau }_0}{2}{\beta }_0^2+{\tau }_0{\mu }_0{\beta }_0-\frac{\tau }{2}N{\beta }_0^2-\tau \sum _{i=1}^N(y_i-{\beta }_1{x}_i){\beta }_0$$
即可以知道
${\beta }_0$的系数为${\tau }_0{\mu }_0+\tau {\sum }_i(y_i-{\beta }_1{x}_i)$
${\beta }_0^2$的系数为$-\frac{{\tau }_0}{2}-\frac{\tau }{2}N$
表示${\beta }_0$的条件采样分布(conditional sampling distribution)为
$${\beta }_0\mid {\beta }_1,\tau ,{\tau }_0,{\mu }_0,x,y\sim \mathcal{N}(\frac{{\tau }_0{\mu }_0+\tau {\sum }_i(y_i-{\beta }_1{x}_i)}{{\tau }_0+\tau N},1/({\tau }_0+\tau N))$$

def sample_beta_0(y, x, beta_1, tau, mu_0, tau_0):assert len(x)==len(y)N = len(y)precision=tau_0 + tau*Nmean = tau_0*mu_0+tau*np.sum(y-beta_1*x)mean /= precisionreturn random.normal(mean, 1/np.sqrt(precision)) # 得到beta_0采样

Update for ${\beta }_1$

条件对数后验方程中关于${\beta }_1$的项为
$$\frac{{\tau }_1}{2}({\beta }_1-{\mu }_1{)}^2-\frac{\tau }{2}\sum _{i=1}^N(y_i-{\beta }_0-{\beta }_1{x}_i{)}^2$$
展开得到
$$-\frac{{\tau }_1}{2}{\beta }_1^2+{\tau }_1{\mu }_1{\beta }_1-\frac{\tau }{2}\sum _i{x}_i^2{\beta }_1^2+\tau \sum _i(y_i-{\beta }_0)x_i{\beta }_1$$
${\beta }_1$的系数为 ${\tau }_1{\mu }_1+\tau {\sum }_i(y_i-{\beta }_0)x_i$，${\beta }_1^2$的系数为$-\frac{{\tau }_1}{2}-\frac{\tau }{2}{\sum }_i{x}_i^2$，所以${\beta }_1$的条件采样密度为
$${\beta }_0\mid {\beta }_1,\tau ,{\tau }_0,{\mu }_0,x,y\sim \mathcal{N}(\frac{{\tau }_0{\mu }_0+\tau {\sum }_i(y_i-{\beta }_1{x}_i)}{{\tau }_0+\tau N},1/({\tau }_0+\tau N))$$

def sample_beta_1(y, x, beta_0, tau, mu_1, tau_1):assert len(x)==len(y)precision=tau_1+tau*np.sum(x*x)mean=tau_1*mu_1+tau*np.sum((y-beta_0)*x)mean/=precisionreturn random.normal(mean, 1/np.sqrt(precision)) 

Update for $\tau$

需要在non-Gaussian distributions下完成对$\tau$值得更新，引入$\Gamma (\alpha ,\beta )$分布
$$p(x;\alpha ,\beta )\propto (\alpha -1)\log x-\beta x$$
带回方程得到
$$p(\tau \mid {\beta }_0,{\beta }_1,y,x)\propto p(y,x\mid {\beta }_0)p(\tau )$$
密度函数为
$$\prod _{i=1}^N\mathcal{N}(y_i\mid {\beta }_0+{\beta }_1{x}_i;1/\tau )\times \Gamma (\tau \mid \alpha ,\beta )$$
有概率密度函数的对数形式可以知道
$$\frac{N}{2}\log \tau -\frac{\tau }{2}\sum _i(y_i-{\beta }_0-{\beta }_1{x}_i{)}^2+(\alpha -1)\log \tau -\beta \tau$$
根据系数可以知道
$$\tau \mid {\beta }_0,{\beta }_1,\alpha ,\beta ,x,y\sim \Gamma (\alpha +\frac{N}{2},\beta +\sum _i\frac{(y_i-{\beta }_0-{\beta }_1{x}_i{)}^2}{2})$$

Synthetic data

设置${\beta }_0=-1,{\beta }_1=2,\tau =1$为真实参数

def synthetic_data():beta_0_true=-1beta_1_true=2tau_true=1N=50x=random.uniform(low=0, high=4, size=N)y=random.normal(beta_0_true+beta_1_true*x, 1/np.sqrt(tau_true))syn_plt=plt.plot(x, y, 'o')plt.xlabel('x(uni. dist.)')plt.ylabel('y(normal dist.)')plt.grid(True)plt.show()

Gibbs sampler

设置${\beta }_0,{\beta }_1$服从先验为$\mathcal{N}(0,1)$，$\tau$服从先验$\Gamma (2,1)$

x, y, N = synthetic_data()# 设置参数起点
init={'beta_0':0, 'beta_1':0, 'tau':2}
# 超参数
hypers={'mu_0': 0, 'tau_0':1, 'mu_1':0, 'tau_1':1, 'alpha':2, 'beta': 1}def gibbs(y, x, iters, init, hypers):assert len(x)==len(y)beta_0, beta_1, tau=init['beta_0'], init['beta_1'], init['tau']param_rec = np.zeros((iters, 3)) # 记录参数的变化for i in range(iters):beta_0=sample_beta_0(y, x, beta_1, tau, hypers['mu_0'], hypers['tau_0'])beta_1=sample_beta_1(y, x, beta_0, tau, hypers['mu_1'], hypers['tau_1'])tau = sample_tau(y, x, beta_0, beta_1, hypers['alpha'], hypers['beta'], N)param_rec[i, :]=np.array((beta_0, beta_1, tau))param_rec = DataFrame(param_rec)param_rec.columns=['beta_0', 'beta_1', 'tau']return param_recdef params():iters=1000 # 设置迭代轮数param_rec = gibbs(y, x, iters, init, hypers)it = [*range(1, iters+1)]beta_0 = param_rec['beta_0'].valuesbeta_1 = param_rec['beta_1'].valuestau = param_rec['tau'].valuesplt.plot(it, beta_0, '-.', color='b', linewidth=1, label='beta_0')plt.plot(it, beta_1, '-.', color='r', linewidth=1, label='beta_1')plt.plot(it, tau, '-.', color='g', linewidth=1, label='tau')plt.grid(True)plt.legend(loc='best')plt.show()params()

得到采样参数变化路径如下
从采样结果可以发现，开始采样时，参数波动比较大，后来逐渐在真实值附近波动.

Even if it is obvious that the variables converge early it is convention to define a burn-in period where we assume the parameters are still converging, which is typically half of iterations. Therefore, we could check the final 500 iterations called trace_burnt

考察采样后半部分的参数

def trace_burnt():iters=1000param_rec = gibbs(y, x, iters, init, hypers)[500:-1]print(param_rec.median()) # 采样得到参数的中位数print(param_rec.std())    # 采样得到参数的标准差hist_plot = param_rec.hist(bins=30, layout=(1, 3))plt.show()

code downlaod

Gibbs sampling python code

References

seaborn画图
Bayesian Data Analysis
Gibbs Sampling
Gibbs sampling for Bayesian linear regression
Markov Chain Monte Carlo(MCMC)
Gibbs采样完整解析与理解