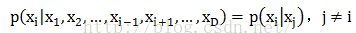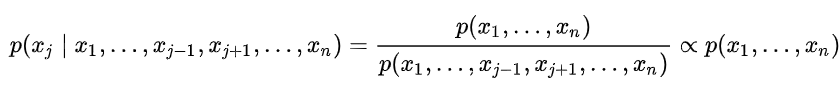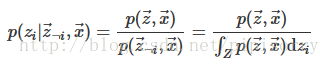
问题
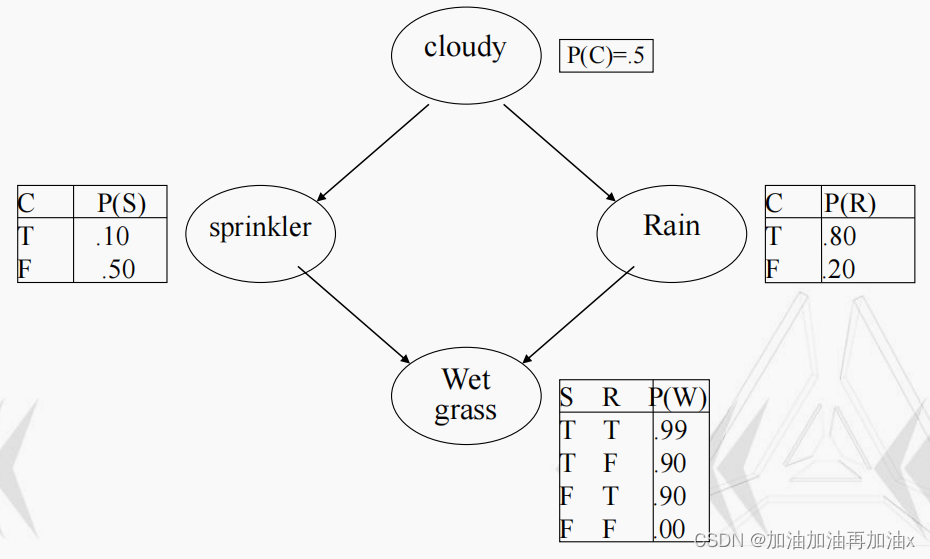
现要求通过吉布斯采样方法,利用该网络进行概率推理(计算 P(R=T|S=F, W=T)、P2(C=F|W=T)的概率值)。
原理
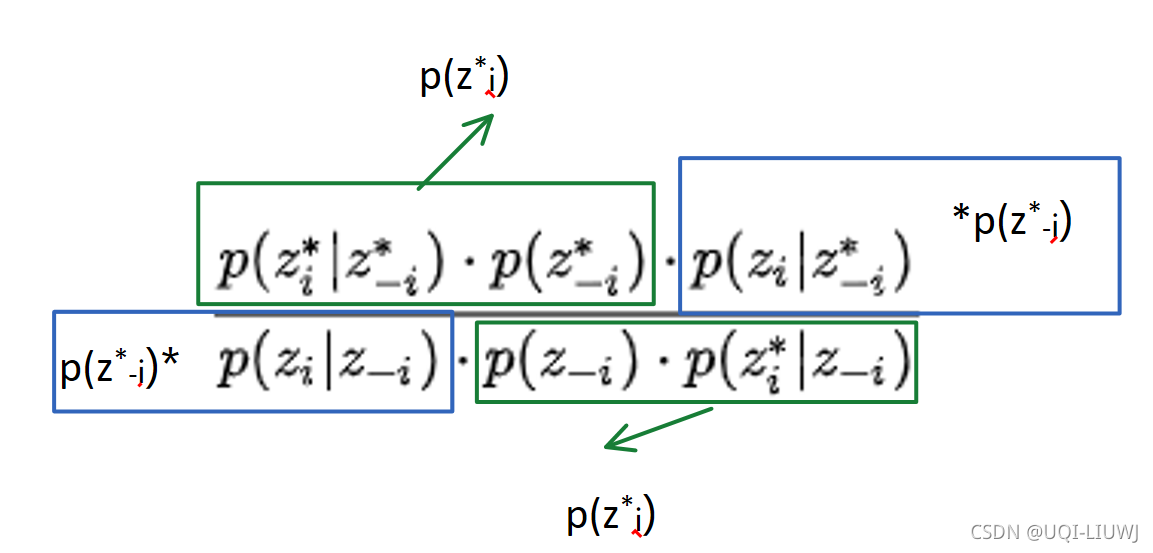
吉布斯采样的核心思想为一维一维地进行采样,采某一个维度的时候固定其他的维度,在本次实验中,假定上一个采样的样本为<C(True)、S(False)、R(True)、W(False)>,此时对C维度进行采样,吉布斯采样将会利用 P(C|S=False,R=True,W=False)的分布得到一个新的 C的值(False),并将该值代替原先的值产生一个新的样本<C(False)、S(False)、R(True)、W(False)>。
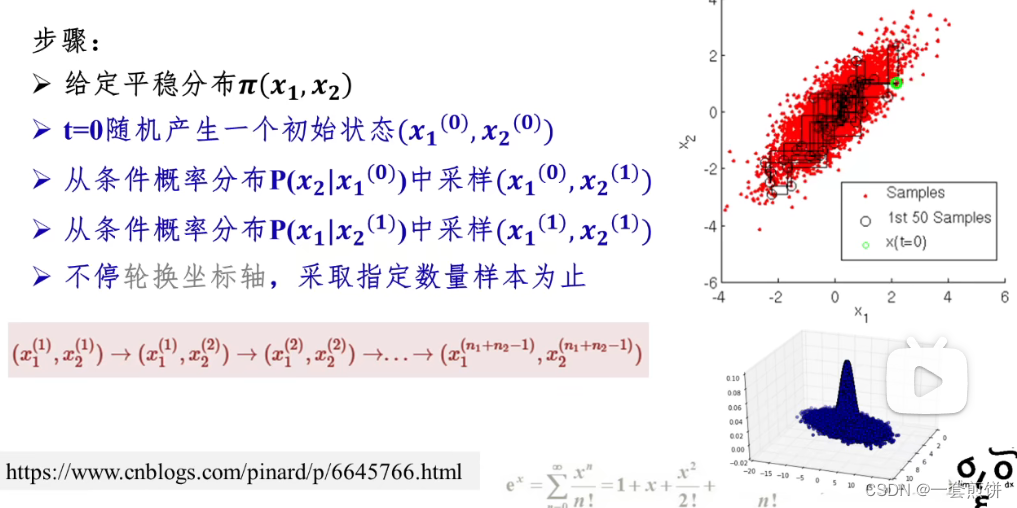
给定分布π(C,S,R,W)
step 1. t=0 时刻产生一个初始状态<C0,S0,R0,W0>,count = 0,采样序列 x=[<C0,S0,R0,W0>]
step 2. 从条件概率分布 P(C|S0,R0)采样得到<C1,S0,R0,W0>,加入到 x[C 已知跳转下一步]
step 3. 从条件概率分布 P(S|C1,R0,W0)采样得到<C1,S1,R0,W0>,加入到 x[S 已知跳转下一步]
step 4. 从条件概率分布 P(R|C1,S1,W0)采样得到<C1,S1,R1,W0>,加入到 x[R 已知跳转下一步]
step 5. 从条件概率分布 P(W|S1,R1)采样得到<C1,S1,R1,W1>,加入到 x[W 已知跳转下一步]
step 6. count = count + 1,如果 count < 指定采样次数跳转到 step2
step 7. 在采样序列中统计满足条件的样本数量,除以总采样数即为所求。
数据结构使用一个 4*2*2*2*2 的矩阵 M 用于存储条件概率分布。如 M[0,:,0,0,0]即表示
P(C|S=False,R=False,W=False)的分布,M[0,:,1,0,0]表示P(C|S=True,R=False,W=False)的分布。该矩阵可通过给定的贝叶斯网络进行构建。
解答
# -*- coding:utf-8 -*-# Gibbs samplingimport numpy as np
import copyclass Gibbs:def __init__(self,query_id=1):self.x = []self.query_id = query_idassert query_id == 1 or query_id ==2self.tran_matrix = np.zeros((4,2,2,2,2))# 0 : C Cloudy# 1 : S Sprinkler# 2 : R Rain# 3 : W Wet grass# 计算条件概率分布# P(C) = 0.5self.tran_matrix[0] = 0.5 # P(C) = 0.5# P(S|C=T) = 0.1,P(S|C=F) = 0.5self.tran_matrix[1,1,0,:,:] = self.tran_matrix[0,1,0,:,:] * (1-0.1)self.tran_matrix[1,1,1,:,:] = self.tran_matrix[0,1,1,:,:] * 0.1self.tran_matrix[1,0,0,:,:] = self.tran_matrix[0,0,0,:,:] * (1-0.5)self.tran_matrix[1,0,1,:,:] = self.tran_matrix[0,0,1,:,:] * 0.5# P(R|C=T) = 0.8,P(R|C=F) = 0.2self.tran_matrix[2,1,:,0,:] = self.tran_matrix[1,1,:,0,:] * (1-0.8)self.tran_matrix[2,1,:,1,:] = self.tran_matrix[1,1,:,1,:] * 0.8self.tran_matrix[2,0,:,0,:] = self.tran_matrix[1,0,:,0,:] * (1-0.2)self.tran_matrix[2,0,:,1,:] = self.tran_matrix[1,0,:,1,:] * 0.2# P(W|S=T,R=T) = 0.99, P(W|S=T,R=F) = 0.9# P(W|S=F,R=T) = 0.9, P(W|S=F,R=F) = 0self.tran_matrix[3,:,1,1,0] = self.tran_matrix[2,:,1,1,0] * (1-0.99)self.tran_matrix[3,:,1,1,1] = self.tran_matrix[2,:,1,1,1] * 0.99self.tran_matrix[3,:,1,0,0] = self.tran_matrix[2,:,1,0,0] * (1-0.9)self.tran_matrix[3,:,1,0,1] = self.tran_matrix[2,:,1,0,1] * 0.9self.tran_matrix[3,:,0,1,0] = self.tran_matrix[2,:,0,1,0] * (1-0.9)self.tran_matrix[3,:,0,1,1] = self.tran_matrix[2,:,0,1,1] * 0.9self.tran_matrix[3,:,0,0,0] = self.tran_matrix[2,:,0,0,0] * (1-0)self.tran_matrix[3,:,0,0,1] = self.tran_matrix[2,:,0,0,1] * 0self.tran_matrix[0] = self.tran_matrix[3] / (self.tran_matrix[3].sum(axis=0,keepdims=True) + 1e-9)self.tran_matrix[1] = self.tran_matrix[3] / (self.tran_matrix[3].sum(axis=1,keepdims=True) + 1e-9)self.tran_matrix[2] = self.tran_matrix[3] / (self.tran_matrix[3].sum(axis=2,keepdims=True) + 1e-9)self.tran_matrix[3] = self.tran_matrix[3] / (self.tran_matrix[3].sum(axis=3,keepdims=True) + 1e-9)# 初始化样本if self.query_id == 1:# P(R=T|S=F,W=T)self.ignore_var_idx = [1,3] # S=F,W=Tself.x.append([True,False,True,True])else:# P(C=F|W=T)self.ignore_var_idx = [3] # W=Tself.x.append([True,False,True,True])self._sample_axis = 0self._var_num = 4def sample(self,sample_num:int):for _ in range(sample_num * (self._var_num - len(self.ignore_var_idx))):last_x = copy.copy(self.x[-1])sample_axis = self._next_sample_axis()last_x[sample_axis]=Truesample_prob = self.tran_matrix[sample_axis,int(last_x[0]),int(last_x[1]),\int(last_x[2]),int(last_x[3])]if np.random.rand() < sample_prob:last_x[sample_axis] = Trueelse:last_x[sample_axis] = Falseself.x.append(last_x)self.x = self.x[::self._var_num - len(self.ignore_var_idx)]def _next_sample_axis(self):self._sample_axis += 1self._sample_axis %= self._var_numwhile self._sample_axis in self.ignore_var_idx:self._sample_axis += 1self._sample_axis %= self._var_numreturn self._sample_axisdef calculate_ans(self):count = 0for x in self.x:if x[2] and self.query_id==1: count += 1if not x[0] and self.query_id==2: count += 1return count / len(self.x)def reset(self):self.x = self.x[:1]gibbs = Gibbs(1)
gibbs.sample(100)
ans = gibbs.calculate_ans()
gibbs.reset()
print('P(R=T|S=F,W=T)采样100次,结果为:',ans)
gibbs.sample(500)
ans = gibbs.calculate_ans()
gibbs.reset()
print('P(R=T|S=F,W=T)采样500次,结果为:',ans)
gibbs.sample(1000)
ans = gibbs.calculate_ans()
gibbs.reset()
print('P(R=T|S=F,W=T)采样1000次,结果为:',ans)gibbs = Gibbs(2)
gibbs.sample(100)
ans = gibbs.calculate_ans()
gibbs.reset()
print('P(C=F|W=T)采样100次,结果为:',ans)
gibbs.sample(500)
ans = gibbs.calculate_ans()
gibbs.reset()
print('P(C=F|W=T)采样500次,结果为:',ans)
gibbs.sample(1000)
ans = gibbs.calculate_ans()
gibbs.reset()
print('P(C=F|W=T)采样1000次,结果为:',ans)运行结果
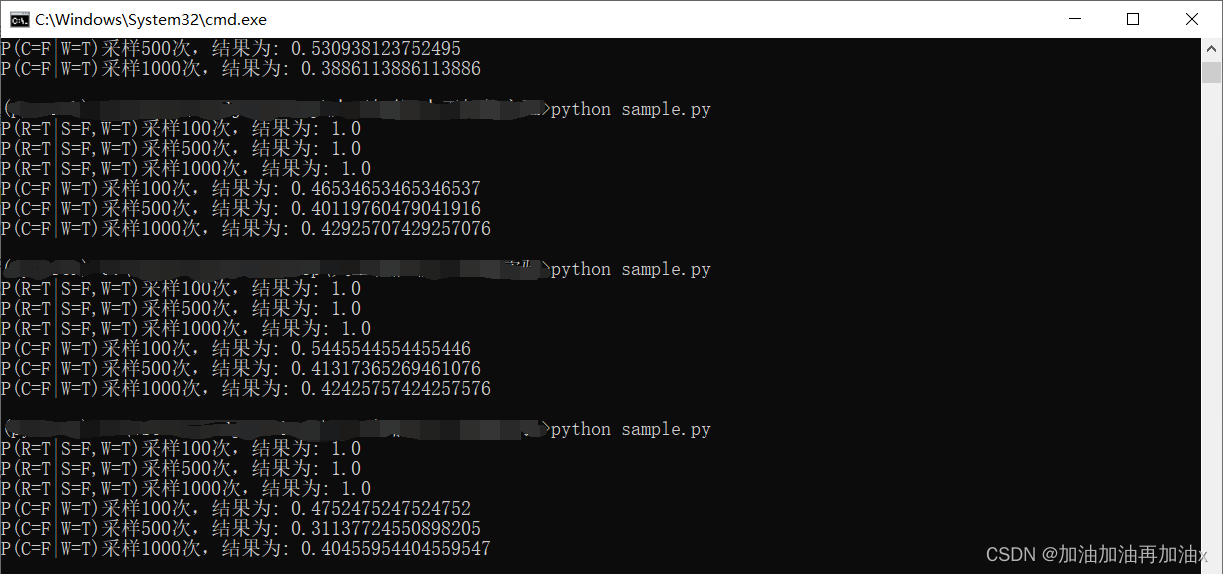
P(R=T|S=F, W=T)≈1
P(C=F|W=T)≈0.41