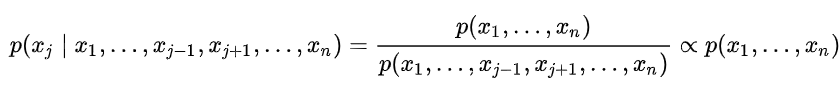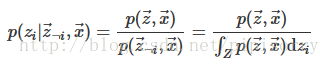吉布斯采样是用条件概率得到联合概率分布。
其实是得到我们想要东西的近似解

1 蒙特卡罗

蒙特卡洛方法是为了解决一些不太好求解的求和或者积分问题。

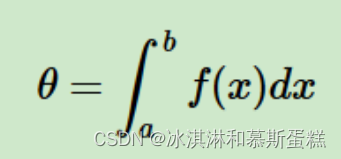
其实就是一个近似方法，通过采样的多个样本代替原本的连续函数，帮助我们把这个式子解出来。
对于一些常见的概率分布p（x），如正态分布等，我们先通过一些公式将其转换为0-1之间的数，（均一化处理嘛，）然后进行采样。
对于不太常见的概率分布f(x)，我们用一个常见的概率分布（如高斯分布）q(x)把他蒙上，就是让 f(x)<=k*q(x),k是常数。
然后对p(x)进行采样得到z₀,，对0到kq(z₀)之间均匀分布采样得到y0,要求接受的样本点（z₀,y₀）不能落在f(z0)和kq(z0)之间，就是下图灰色区域，灰色是拒绝区域。（图来自参考链接）
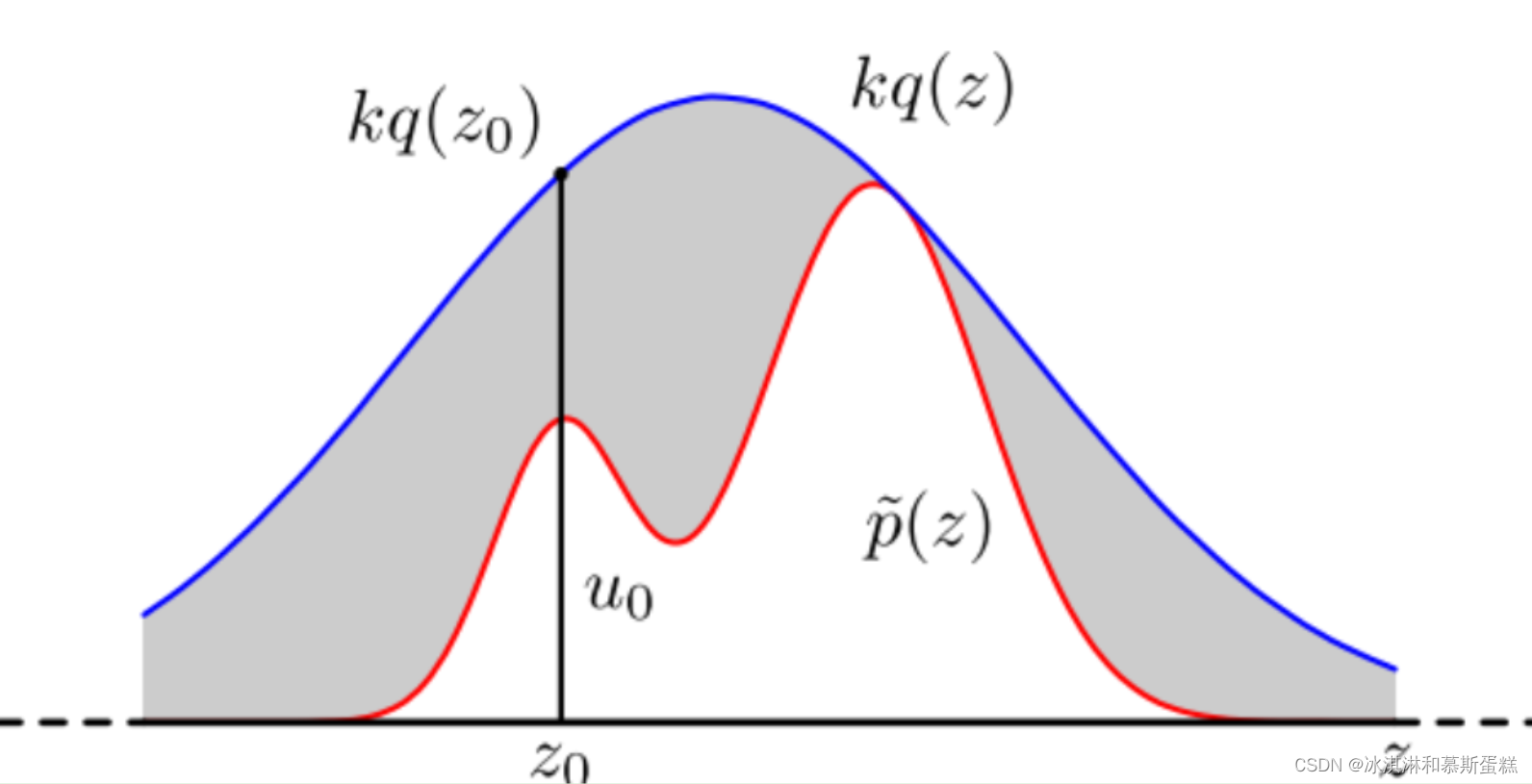这里其实我还是不太理解怎么就可以用不断的接受拒绝q来模拟p了，
最终的结果公式：（蒙特卡洛一般形式 p是概率分布，f是要求积分的公式，n是采样n次）

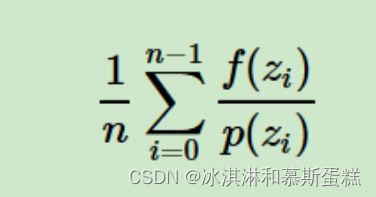
参考：MCMC(一)蒙特卡罗方法

2 马尔科夫链

马尔科夫链接触过很多次了，就是说下一个时刻的状态只依赖于前一个时刻的状态。
马尔科夫状态转移矩阵P，我们假设其中p(i,j)是状态i到状态j转移的概率，比如状态i是吃饭，状态j是拉肚子，那么p(i,j)==0.35就是吃饭后拉肚子的概率是0.35.
马尔科夫链的一个性质是，经过非常多次状态转换后，我们得到的最终的状态分布和初始状态分布关系不大，只和状态转移矩阵有关，最终的状态概率分布比较稳定。

要求：
非周期的马尔科夫链，如果是周期的不会收敛。
任意两个状态是联通的，就是通过有限个步骤可以到达的。
马尔科夫链的状态数可以是有限的或者是无限的（无限的比如连续函数）
如果上一个状态向量T，则最终稳定时的状态分布 TP=T，T为马尔科夫链的平稳分布。

马尔科夫链的采样：
1.得到状态转移矩阵P，采样（任意简单概率分布都可以）得到初始状态概率分布x0，设置状态转移次数阈值n1，需要的样本个数n2；
2.for t =0 to n1+n2-1 ，从条件概率分布p(x|x_t)中采样得到样本x _t+1;
我们需要的平稳分布对应的样本集就是（x_n1,x_n1+1,x_n1+2,…x _n1+n2-1）

就是要通过这些样本集，进行蒙特卡洛模拟，得到马尔科夫链中的平稳分布，就是TP中的T。

这里我不太理解，为什么需要蒙特卡洛模拟 ，这里最终采样得到的X应该都接近于T了，也就是说，只要把所有的样本累加除以n2就可以了吧？
这里如果带入蒙特卡洛一般公式的话这里的p是谁呢?怎么得到呢？

参考：MCMC(二)马尔科夫链

3.MCMC采样

MCMC采样是想要通过马尔科夫链的平稳分布获得马尔可夫链的转移矩阵。

MCMC算法过程如下：
1.获得平稳分布T，任意选定的转移矩阵Q，采样（任意简单概率分布）得到初始状态概率分布x0，设置状态转移次数阈值n1，需要的样本个数n2；
2.for t =0 to n1+n2-1 ，
从 条件概率分布Q(x|x_t) 中采样得到样本x_t+1;
从均匀分布（0，1）采样u
如果u< $\alpha$（x_t,x_*）, 其中$\alpha$（x_t,x_*）=T（x_*）Q（x _* , x_t），
则接受转移 x_t -> x_* 就是 x_t+1=x_*,
否则不接受转移， x_t+1=x_t
样本集就是（xn1,xn1+1,xn1+2,…x n1+n2-1）
这里的接受拒绝也没看懂，就是为什么要用u来进行比较，这里的u进行多次采样，采样本身应该是符合高斯分布的。只能大概有这个感觉。

链接：MCMC(三)MCMC采样和M-H采样

4 MH采样

MH采样解决了MC接受率过低的问题。
对上面的 $\alpha$（x_t,x_*）进行了改进，
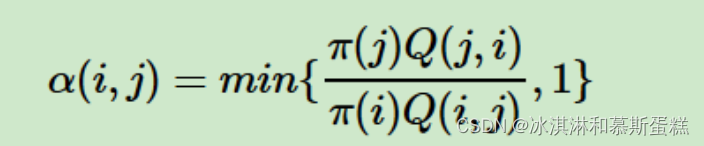这样的话就是让u更容易小于$\alpha$，更容易被接受，其余和 MCMC没有区别

5 吉布斯采样

定义：
吉布斯采样（英语：Gibbs sampling）是统计学中用于马尔科夫蒙特卡洛（MCMC）的一种算法，用于在难以直接采样时从某一多变量概率分布中近似抽取样本序列。该序列可用于近似联合分布、部分变量的边缘分布或计算积分（如某一变量的期望值）。某些变量可能为已知变量，故对这些变量并不需要采样。
来源：维基百科定义

吉布斯采样程序的每一步都涉及用某个变量相对于其他变量的条件概率分布中抽样得出的值代替该变量的值。

具体方法
  首先随便初始化一个组合,i.e. 学习+晚上+刮风，
  然后依条件概率改变其中的一个变量。
  具体说，假设我们知道晚上+刮风，我们给E生成一个变量，比如，学习-》吃饭。我们再依条件概率改下一个变量，根据学习+刮风，把晚上变成上午。类似地，把刮风变成刮风（当然可以变成相同的变量）。这样学习+晚上+刮风-》吃饭+上午+刮风。
  同样的方法，得到一个序列，每个单元包含三个变量，也就是一个马尔可夫链。然后跳过初始的一定数量的单元（比如100个），然后隔一定的数量取一个单元（比如隔20个取1个）。这样sample到的单元，是逼近联合分布的。
  
来源：csdn_吉布斯采样（Gibbs Sampling）

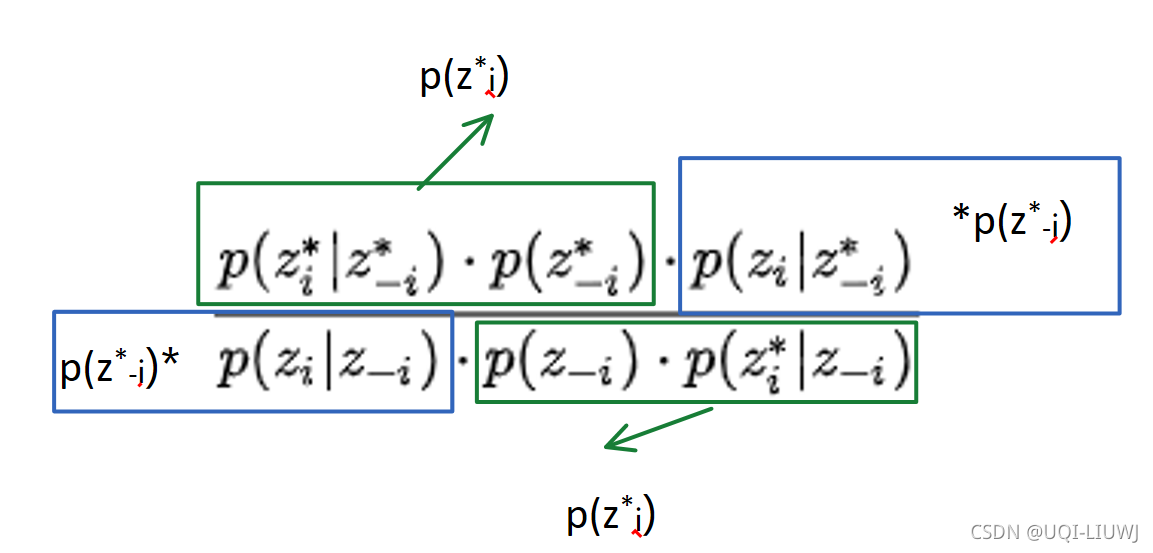
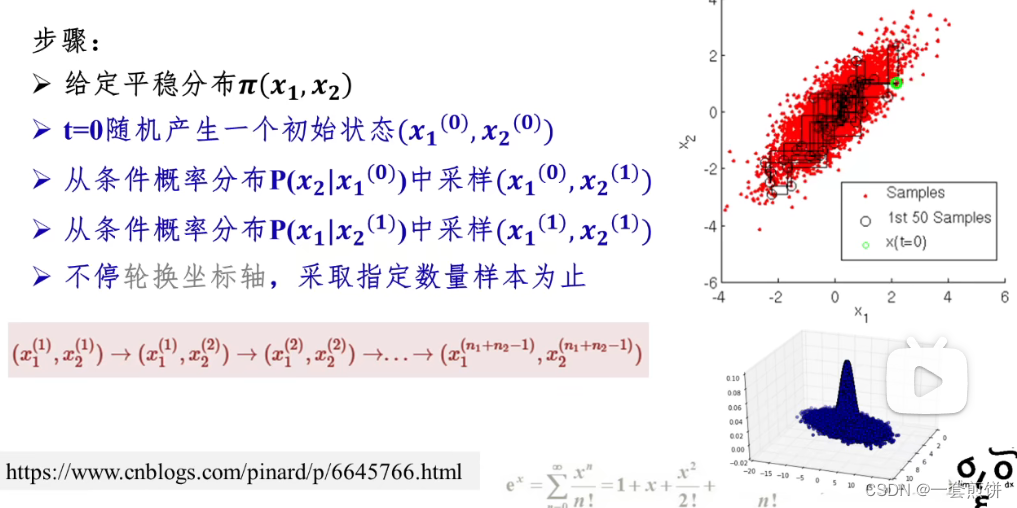
也就是，吉布斯采样采用的是坐标轴轮换（维度轮换）的思维进行采样，每次固定某个轴a，以其他轴为 条件 进行采样，预测a在t+1时刻的值。
参考：MCMC(四)Gibbs采样