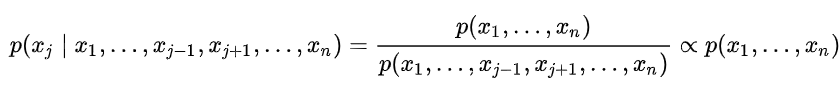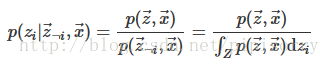原文来自：https://victorfang.wordpress.com/2014/04/29/mcmc-the-gibbs-sampler-simple-example-w-matlab-code/

【注】评论区有同学指出译文理论编码有误，请参考更官方的文献，个人当时仅验证过红色字体部分理论与维基百科中二位随机变量吉布斯采样的结果是否对应，其余部分有意见希望可以详细指出，大家互相交流。

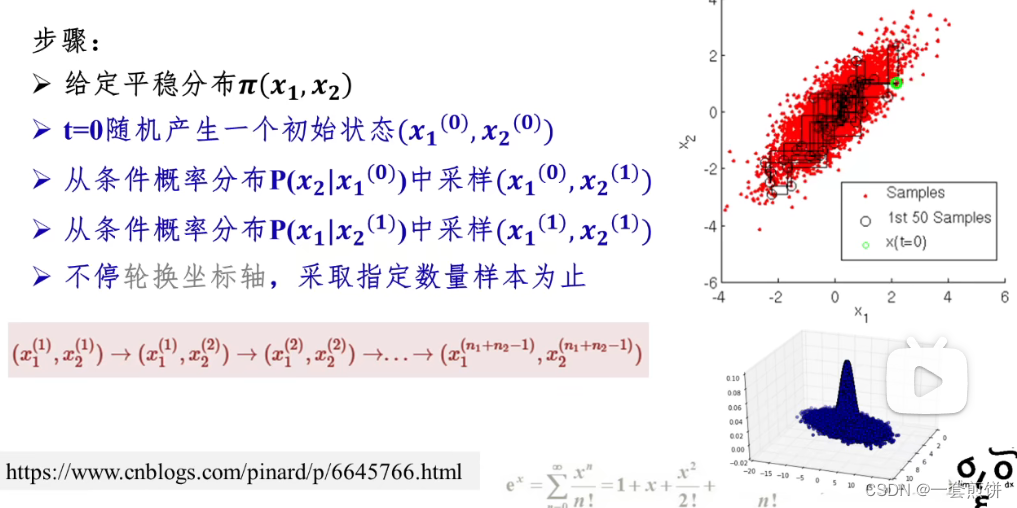
MCMC(马尔可夫链蒙特卡洛方法)：the Gibbs Sampler(吉布斯采样)

在之前的博客中，我们对比了在一个多元概率分布p(x)中，分别采用分组(block-wise)和分成分(component-wise)实现梅特罗波利斯哈斯廷斯算法。对于多元变量问题中的MCMC算法，分成分更新权重比分组更新更有效，因为通过使每一个成分/维度独立于其他成分/维度，我们将更可能去接受一个提议采样【注，这个proposed sample应该就是前面博客里面提到的转移提议分布】。然而，提议采样仍然可能被拒绝，导致有些多余的计算，因为他们被拒绝了，计算了但是一直未使用。吉布斯采样是另外一种比较受欢迎的MCMC采样技术，提供了避免这种多余计算的方法。就像分成分实现Metropolis Hastings算法，吉布斯仍然使用分成分更新。然而，不像Metropolis Hastings采样，所有的提议采样将被接受，因此不会有多余的计算。

基于两个标准，吉布斯采样使用某些类别的问题。给定一个目标分布p(x)，其中

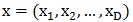，第一个标准是以其它所有变量联合起来的联合分布为条件的每一个变量的条件分布有解析(数学)表达式。在形式上，如果目标分布p(x)是D维的，我们必须有D个独立的表达式：

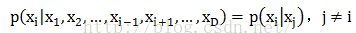
每一个表达式都定义了在知道其他j(j≠i)维的数值的情况下第i维的概率。具有每一个变量的条件分布代表我们不需要像Metropolis Hastings算法需要提议分布或者接受/拒绝标准。因此，当其他变量固定的时候，我们可以简单的从每一个条件中去采样。第二个标准就是我们必须能够从每一个条件分布中去采样。如果我们想要去实现一个算法，这个附加条件是非常明显的。

吉布斯采样的工作方法与分成分Metropolis Hastings算法很像，除了取缔借鉴每一个维度的提议分布