本专栏包含信息论与编码的核心知识，按知识点组织，可作为教学或学习的参考。markdown版本已归档至【Github仓库：information-theory】，需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。

霍夫曼编码

最佳变长编码

• 最佳码: 对于某一信源和某一码符号集来说,若有一唯一可译码,其平均码长小于所有其他唯一可译码的平均长度。
• 紧致码
  • 香农(Shannon)
  • 费诺(Fano）
  • 霍夫曼(Huffma )

霍夫曼编码

在霍夫曼编码算法中, 固定长度的信源输出分组将映射成可变长度的二进制分组。该过程称为定长到变长编码。

其思想是将频繁出现的固定长度序列映射成较短的二进制序列, 而将出现频率较低的固定长度序列映射成较长的二进制序列。

平均码长
$$\overline{\mathbf{K}}=E[L]=\sum _{x\in \Xi }p(x)l(x)$$
一种最优的信源编码方法是信源的平均码长接近或者等于信源的信息熵H(X) 。

霍夫曼编码的步骤

1. 将信源消息符号按其出现的概率大小依次排列 $p(x_1)\ge p(x_2)\ge \dots \ge p(x_n)$
2. 取两个概率最小的字母分别配以 0 和 1 两码元, 并将这两个概率相加作为一个新字母的概率, 与未分配的二进 符号的字母重新排队。
3. 对重排后的两个概率最小符号重复步骤(2)的过程。
4. 不断继续上述过程,直到最后两个符号配以 0 和 1 为止
5. 从最后一级开始,向前返回得到各个信源符号所对应的码元序列, 即相应的码字。

Example：试为如下信源设计霍夫曼编码

$$\left[\begin{array}{l}\mathrm{A}\\ P\end{array}\right]=\left[\begin{array}{ccccc}A1& A2& A3& A4& A5\\ 1/2& 1/4& 1/8& 1/16& 1/16\end{array}\right]$$

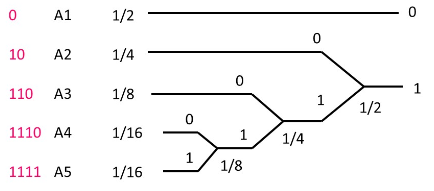
上例中, 平均码长为
$$\begin{array}{l}\bar{K}=E(L)=1\times 1/2+2\times 1/4+3\times 1/8+2\times 4\times 1/16\\ =1.875\\ H(X)=1.875=E(L).\end{array}$$
霍夫曼编码的平均码长满足如下不等式
$$H(X)\le \overline{\mathbf{K}}<H(X)+1$$
如果对长度为n的信源字符序列进行霍夫曼编码(信源的 n 次扩展信源) 而不是对单信源字符的编码, 则有

$$H(X^n)\le {\overline{\mathbf{K}}}_n<H(X^n)+1$$

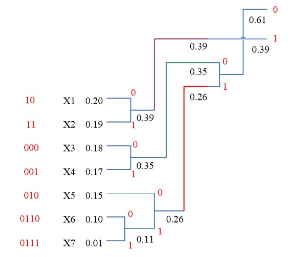
例 设单符号离散无记忆信源如下. 要求对信源编二进制霍夫曼码。
$$\left[\begin{array}{l}X\\ p(x)\end{array}\right]=\left[\begin{array}{ccccccc}{x}_l& x_2& x_3& x_4& x_5& x_6& x_7\\ 0.20& 0.19& 0.18& 0.17& 0.15& 0.10& 0.01\end{array}\right]$$

熵
$$\begin{array}{l}H(X)\\ \begin{array}{rl}=-0.2& \log 0.2-0.19\log 0.19-0.18\log 0.18-0.17\log 0.17\\ & -0.15\log 0.15-0.10\log 0.10-0.01\log 0.01\\ =& 2.61\end{array}\end{array}$$
平均码长为
$$\begin{array}{l}\bar{K}={\sum }_{i=1}^{7}p\left(x_i\right)K_i\\ =0.2\times 2+0.19\times 2+0.18\times 3+0.17\times 3+0.15\times 3+0.10\times 4+0.01\times 4=2.72\end{array}$$
编码效率
$$\eta =\frac{H(X)}{R}=\frac{H(X)}{\bar{K}}=\frac{2.61}{2.72}=96\%$$

霍夫曼的编法并不唯一。每次对缩减信源两个概率最小的符号分配“0”和“1”码元是任意的,所以可得到不同的码字。只要在各次缩减信源中保持码元分配的一致性,即能得到可分离码字。不同的码元分配,得到的具体码字不同,但码长$K_i$不变,平均码长也不变,所以没有本质区别;

缩减信源时,若合并后的新符号概率与其他符号概率相等，从编码方法上来说,这几个符号的次序可任意排列,编出的码都是正确的,但得到的码字不相同。

不同的编法得到的码字长度$K_i$也不尽相同。

例 单符号离散无记忆信源

[ X P ( X ) ] = { x 1 , x 2 , x 3 , x 4 , x 5 0.4 0.2 0.2 0.1 0.1 } [\begin{array}{c} X \\ P(X) \end{array}]=\{\begin{array}{lllll} x_{1}, & x_{2}, & x_{3}, & x_{4}, & x_{5} \\ 0.4 & 0.2 & 0.2 & 0.1 & 0.1 \end{array}\} [XP(X)​]={x1​,0.4​x2​,0.2​x3​,0.2​x4​,0.1​x5​0.1​}

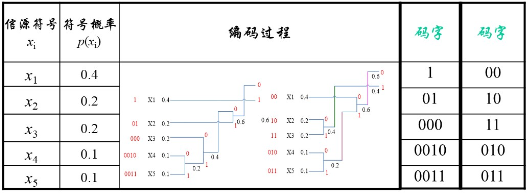
单符号信源编二进制哈夫曼码,编码效率主要决定于信源熵和平均码长之比。

对相同的信源编码, 其熵是一样的, 采用不同的编法, 得到的平均码长可能不同。

平均码长越短,编码效率就越高。

编法一的平均码长为
$$\overline{K_1}=\sum _{i=1}^{5}p\left(x_i\right)K_i=0.4\times 1+0.2\times 2+0.2\times 3+0.1\times 4\times 2=2.2$$
编法二的平均码长为
$$\overline{K_2}=\sum _{i=1}^{5}p\left(x_i\right)K_i=0.4\times 2+0.2\times 2\times 2+0.1\times 3\times 2=2.2$$
两种编法的平均码长相同,所以编码效率相同。

哪种方法更好?

定义码字长度的方差 ${\sigma }^2$ :
$$\begin{array}{c}{\sigma }^2=E\left[{\left(K_i-\bar{K}\right)}^2\right]={\sum }_{i=1}^{5}p\left(x_i\right){\left(K_i-\bar{K}\right)}^2\\ {\sigma }_1^2=0.4(1-2.2{)}^2+0.2(2-2.2{)}^2+0.2(3-2.2{)}^2+0.1(4-2.2{)}^2\times 2=1.36\\ {\sigma }_2^2=0.4(2-2.2{)}^2+0.2(2-2.2{)}^2\times 2+0.1(3-2.2{)}^2\times 2=0.16\end{array}$$
第二种编码方法的码长方差要小许多。第二种编码方法的码长变化较小, 比较接近于平均码长。

第一种方法编出的5个码字有4种不同的码长;第二种方法编出的码长只有两种不同的码长;第二种编码方法更简单、更容易实现,所以更好。

结论:

在霍夫曼编码过程中,对缩减信源符号按概率由大到小的顺序重新排列时,应使合并后的新符号尽可能排在靠前的位置, 这样可使合并后的新符号重复编码次数减少,使短码得到充分利用。

例: 一信源模型如下, 试对信源符号进行 Huffman编码, 并计算平均码长和编码效率 。若对其2次扩展信源进行编码, 结果如何

$$\left[\begin{array}{l}S\\ p\end{array}\right]=\left[\begin{array}{ccccc}{s}_1& s_2& s_3& s_4& s_5\\ 0.4& 0.2& 0.2& 0.1& 0.1\end{array}\right]$$
解: (1) 不做扩展, 进行单符号Huffuman编码时 编码结果为:
$$\begin{array}{ccc}{s}_1& 1& \\ s_2& 01& H(S)=2.122bit/sym\\ s_3& 000& \bar{l}=2.2\text{ 码元 }/\text{ sym }\\ s_4& 0010& \eta =H(S)/\bar{l}=0.965\\ s_5& 0011& \end{array}$$
（2）二次扩展信源 ${\mathrm{S}}^2$ , 共有 $5^2=25$ 个信源符号, 为
$$\begin{array}{l}{s}_1{s}_1,s_1{s}_2,s_1{s}_3,s_1{s}_4,s_1{s}_5,s_2{s}_1,s_2{s}_2,s_2{s}_3,s_2{s}_4,s_2{s}_5\\ s_3{s}_1,s_3{s}_2,s_3{s}_3,s_3{s}_4,s_3{s}_5,s_4{s}_1,s_4{s}_2,s_4{s}_3,s_4{s}_4,s_4{s}_5\\ s_5{s}_1,s_5{s}_2,s_5{s}_3,s_5{s}_4,s_1{s}_5\end{array}$$
双应的概率为: $0.16,0.08,0.08,0.04,0.04\cdots 0.01$ 可得编码结果为

$$\begin{array}{l}{s}_1{s}_1(01),s_4{s}_2(001),s_1{s}_3(1001),s_1{s}_4(0001),s_4{s}_5(10111),\\ s_2{s}_1(1000),s_2{s}_2(11001),s_2{s}_3(11010),s_2{s}_4(111010),s_2{s}_5(111011)\\ s_3{s}_1(1010),s_3{s}_2(11011),s_3{s}_3(11100),s_3{s}_4(111110),s_3{s}_5(111111),\\ s_4{s}_1(10110),s_4{s}_2(111100),s_4{s}_3(000000),s_4{s}_4(00001000),s_4{s}_5(0000101),\\ s_5{s}_1(11000),s_5{s}_2(111101),s_5{s}_3(000001),s_5{s}_4(0000110),s_5{s}_5(0000111)\\ \bar{l}=2.16\text{ 码无/sym }\\ \eta =0.982\end{array}$$
结论：N 越大, 编码效率越大。

某DMS信源如式: $\left[\begin{array}{l}\mathrm{X}\\ \mathrm{P}\end{array}\right]=\left[\begin{array}{ccc}{x}_1& x_2& x_3\\ 1/2& 1/3& 1/6\end{array}\right]$ , 则其二次扩展信源为

$$\begin{array}{l}\left[\begin{array}{c}{X}^2\\ P\end{array}\right]=\left[\begin{array}{ccccccccc}{x}_1{x}_1& x_1{x}_2& x_1{x}_3& x_2{x}_1& x_2{x}_2& x_2{x}_3& x_3{x}_1& x_3{x}_2& x_3{x}_3\\ 1/4& 1/6& 1/12& 1/6& 1/9& 1/18& 1/12& 1/18& 1/36\end{array}\right]\end{array}$$
请分别对DMS信源: $\left[\begin{array}{l}\mathrm{X}\\ \mathrm{p}\end{array}\right]=\left[\begin{array}{ccc}{x}_1& x_2& x_3\\ 1/2& 1/3& 1/6\end{array}\right]$ , 及其二次扩展信源进行二进制霍夫曼编码，并计算平均码长。

DMS信源: $x_1-1;x_2-01;x_3-00$ 。平均码长 =1.5

扩展信源:

$\begin{array}{ccccccccc}{x}_1{x}_1& x_1{x}_2& x_1{x}_3& x_2{x}_1& x_2{x}_2& x_2{x}_3& x_3{x}_1& x_3{x}_2& x_3{x}_3\\ 1/4& 1/6& 1/12& 1/6& 1/9& 1/18& 1/12& 1/18& 1/36\\ 01& 111& 001& 110& 100& 1000& 1011& 0011& 0010\end{array}$

平均码长 =107 / 36; 平均每符号码长 =107 / 72=1.486;

该信源信息熵 =1.459 bit/sym。

L-Z编码

将信源序列分成一系列以前未出现而且最短的字符串或词组。如，将信源序列列1011010100010…分成1，0，11，01，010，00，10，…注意，每个词组具有如下性质:

• 每个词组有一个前缀在前面出现过;
• 每个词组的长度比其前缀长一个字符。
• 对词组进行如下编码:给出前缀在词组序列中的位置号和最后一个字符的值。L-Z编码先将信源分成不等长的词组然后编码。

设c(n)为信源序列所分成的词组的个数，那么描述词组的前缀的位置需要logc(n) bit, 而词组的最后一个符号需要1bit。上例中，词组的个数为7，那么描述词组的前缀的位置需要3bit。所对应的编码序列为（000，1)，（000，0)(001，1) , (010，1) ,（100，0) , (010，0)，(001，0)。其中每个括号内的第一个数字表示该词组的前缀的位置序号，第二个数字是该词组的最后一个符号。

L-Z算法主要包括两步:

1. 将序列分组，计算词组个数c(n)和描述前缀的位置需要的比特数logc(n);
2. 对每个词组，计算前缀位置，构成码字。前缀位置的编码可以是等长码，也可以是变长码。通常在起始位置需要的位数少，而随着词组序号的增长，前缀位置的编码的位数也不断增加。L-Z编码一般用在信源序列长度较大是才有效。

总结

• 编码的基本概念
• 无失真信源编码:译码错误概率任意小。
• 香农无失真信源编码定理:存在压缩编码的极限。
• 霍夫曼编码:是一种最优的信源编码，某些信源概率分布条件下，可以达到香农信源编码的极限。

参考文献：

1. Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
2. Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
3. 周炯槃. 通信原理（第3版）[M]. 北京：北京邮电大学出版社, 2008.
4. 樊昌信, 曹丽娜. 通信原理（第7版） [M]. 北京：国防工业出版社, 2012.