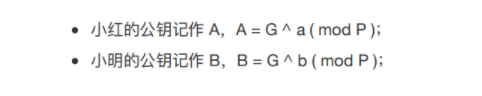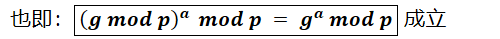DH 算法是 Diffie和Hellman于1976年提出了一种的密钥交换协议。这种加密算法主要用于密钥的交换，可以在非安全信道下为双方创建通信密钥，通讯双方可以使用这个密钥进行消息的加密、解密，并且能够保证通讯的安全。

换而言之，算法希望实现这样的一个效果：

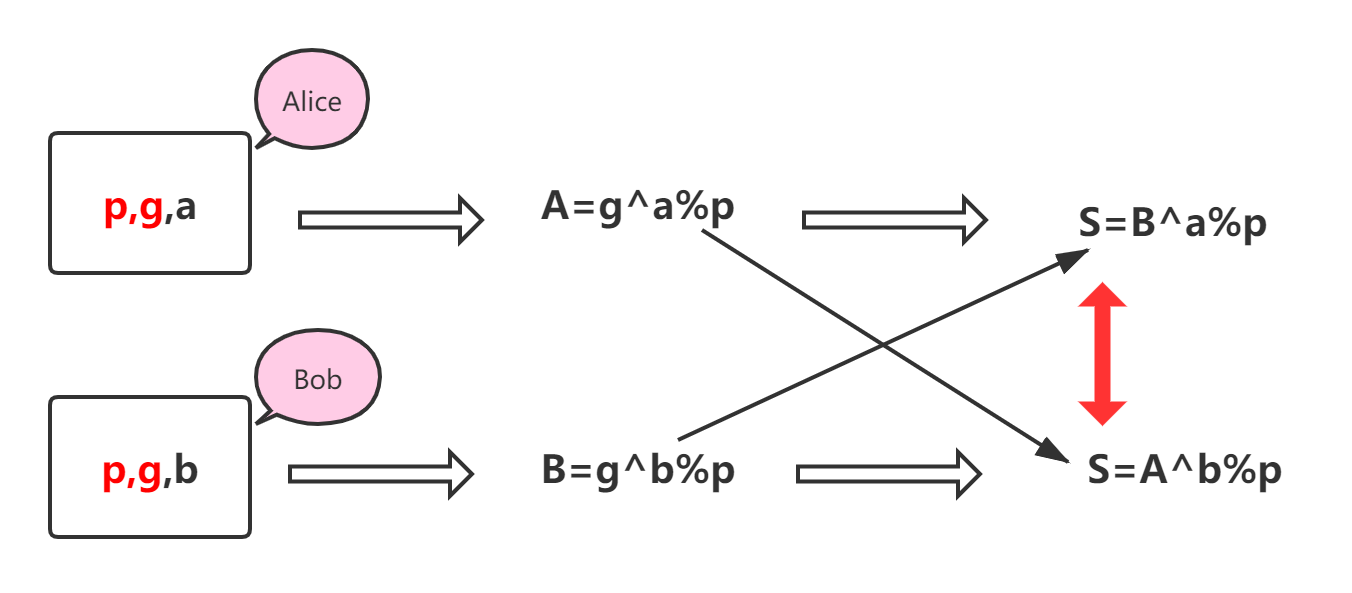
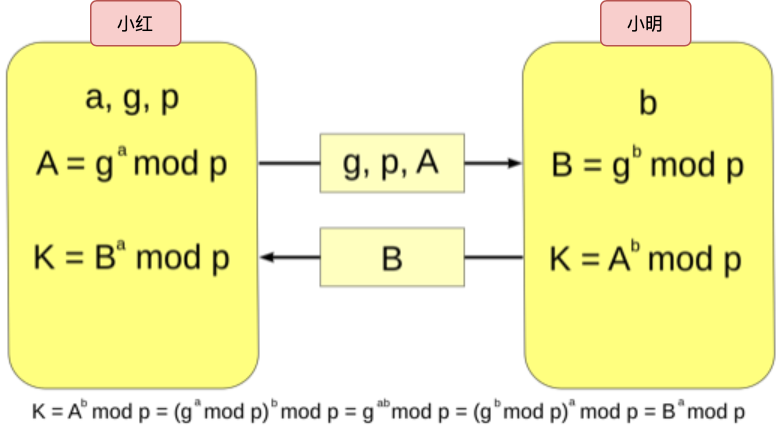
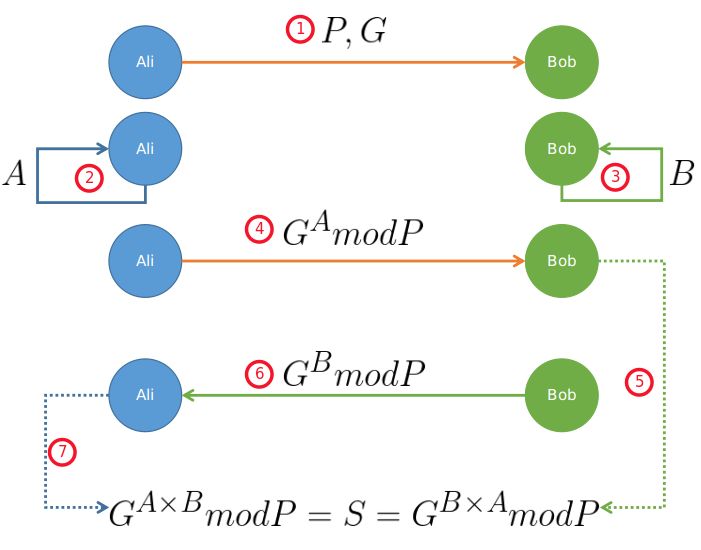
通信方A和B首先各自生成密钥$D_a$和$D_b$，然后通过某种计算获得各自的公钥$P_a$和$P_b$，接下来，A和B互相交换公钥$P_a$和$P_b$。现在，A持有自己的密钥$D_a$和B的公钥$P_b$，B持有自己的密钥$D_b$和A的公钥$P_a$，$D_a$与$P_b$、$D_b$与$P_a$经过某种数学运算，都能生成一个相同的加密密钥S用于通信。正在监听通信的第三方由于只得到了$P_a$和$P_b$，是无法计算得出密钥S的。

具体的过程如下图所示：

公钥$P_a$和$P_b$由函数$f_1$计算得出，共享密钥由$f_2$计算得出。这两个函数的破解难度直接影响到整个密钥交换算法的强度。

不妨选择函数为$f_2(a,b)=ab$，也就是说我们需要让等式$D_a{P}_b=D_b{P}_a$成立（否则无法生成相同的密钥）。现在我们随便选择一个常量因子F，令函数$f_1(x)=F\cdot x$，则有$D_{a}F{D}_b=D_{b}F{D}_a$，等式$D_a{P}_b=D_b{P}_a$成立了。

现在我们得出了一个简单的密钥交换策略：双方都先约定好一个常数F，假设为100好了，然后A和B各自随机生成一个密钥，假设$D_a=3$，$D_b=4$，按照函数$f1$生成公钥$P_a=300$，$P_b=400$，然后互相交换。现在A知道$D_a$和$P_b$，一乘起来就是1200，B那边也是，$D_b\cdot P_a=1200$，这个1200就是他们的共享密钥S。

如果只得知双方交换的公钥，是无法得出密钥S的，但是F被第三方得知的话，通信加密就会立刻被破坏。首先，这个常数F不能固定写在程序内，因为程序一旦发布，这个固定的常数就有暴露的风险，更糟糕的是，F暴露之后所有使用这个常数的会话都变得不安全了。而每次会话随机选择一个常数F，面临的问题则是双方如何在不安全信道交换F。

上述简单策略不能实现密钥交换的原因是算法过于简单并且可逆。若是只是简单的使用加减乘除进行多项式计算，基本都是可逆且能够快速计算出来的。因此，如何防止别人利用从公钥$P_a$、$P_b$根据函数$f_1$进行逆向分解得出A或B的密钥，即不可逆，同时又可以让A和B根据公钥生成公共的密钥成了关键。（就算函数$f_1$不出现在网络中，但在最坏的情况下函数$f_1$会暴露）。

生成公钥的$f_1$有两种实现方式：基于离散对数难题的最早版本的DH算法，和结合了椭圆曲线问题的加强版算法ECDH。

基于离散对数难题的DH算法

要实现不可逆的目标，其实也就是令函数$f_1$没有反函数，例如$f(x)=x^2$在定义域$R$上没有反函数。当然，只是没有反函数的话强度是不够的，$y=x^2$中的y只有两种可能的x取值，稍微用密文试试手就知道x和-x谁才是密钥了。一个y最好对应无穷个x的值，例如$y=x\mathrm{m}\mathrm{o}\mathrm{d}p$，但是这样还不够，仍存在被暴力破解的风险。

$f_1$实现如下，它利用了离散对数问题的难解性：

选择一个二元组$(g,p)$，定义函数$f_1(x)=g^x\mathrm{m}\mathrm{o}\mathrm{d}p$，其中$x\in (1,p)$且为整数，作为公钥生成的函数。

这其中g和p都是一个常数。假设窃听者得知了公钥$P_a$，想要计算$D_a$的话，不妨设$n\in N$，然后有：
$$g^{D_a}=n\cdot p+P_a\to D_a={\log }_g(n\cdot p+P_a)$$
想要解答上述算式存在时间上的问题，对于精心挑选的的g和p而言，没有多项式时间的经典算法可用于破解它们。

如何选择二元组(g,p)

如果并不关心算法参数的具体实现，这一节内容可以跳过。

二元组需要满足什么条件，才不会被轻易破解呢？

假设我们选择了一个二元组(2,7)，不妨使用函数$f_1$计算一下：
$$\begin{gathered} 2^1\mathrm{m}\mathrm{o}\mathrm{d}7=2 \\ {2}^2\mathrm{m}\mathrm{o}\mathrm{d}7=4 \\ {2}^3\mathrm{m}\mathrm{o}\mathrm{d}7=1 \\ {2}^4\mathrm{m}\mathrm{o}\mathrm{d}7=2 \end{gathered}$$
$2^x\mathrm{m}\mathrm{o}\mathrm{d}7$的值存在一个循环，这可不是什么好消息，攻击者无需遍历1~p就有可能猜出密钥！

上面的循环，我们专门用阶来定义这种概念。

阶的定义：m为正整数，若$(a,m)=1$，使得$a^d\mathrm{m}\mathrm{o}\mathrm{d}m=1$成立的最小正整数d，被称为a对模m的阶，记作$or{d}_m(a)$。$(a,m)$的含义为a与m互质。

我们可以证明，$a,a^2,\cdots a^{or{d}_m(a)}$mod $m$的值两两不相等（或者说它们互不同余）。那么要想加强算法的强度，阶d最好应当等于m-1，这样意味着$a^d\mathrm{m}\mathrm{o}\mathrm{d}m$的取值范围为$[1,m-1]$，达到了最大化。

想要达到这个目的，我们还得回答一个问题：$$a^d\mathrm{m}\mathrm{o}\mathrm{d}m$$中，对于任意一个m而言，a存在某个值，使得其阶d等于m-1吗？

要回答这个问题，需要引入欧拉函数的概念：

对于正整数n，欧拉函数$\phi (x)$是小于n的正整数中与n互质的数的数目。

例如$\phi (10)=4$，与它互质的数分别为1、3、7、9。而$\phi (7)=6$，对于质因数x而言，$\phi (x)=x-1$。

下面的欧拉定理能部分回答我们的问题：
$$若a,m均为正整数,(a,m)=1,则a^{\phi (m)}\mathrm{m}\mathrm{o}\mathrm{d}m=1$$

上面的定理实际上告诉了我们a对模m的阶的最大值至多为$\phi (m)$。例如对于模15来说，不管如何选择底数a，它的阶最大也只可能是$\phi (15)=8$，而不可能是我们期望的最好的值14。要想达到最好的效果，模m就必须选择一个奇质数（2是质数但它太小了），这样$\phi (m)=m-1$，才有希望取到最大的阶。

不过问题还没回答完，对于某个确定的模m（比如说7），真的存在一个数a，它的阶是$\phi (m)$吗？请不要把这个问题和上面的欧拉定理混淆，虽然$a^{\phi (m)}\mathrm{m}\mathrm{o}\mathrm{d}m=1$（欧拉定理）必定成立，但是不代表值$\phi (m)$是a的阶啊！

举一个很明显的例子，假设a=2，p=7，我们很容易得知$\phi (7)=6$，而$2^6\mathrm{m}\mathrm{o}\mathrm{d}7=1$，欧拉定理确实是成立的，但重新再看看上面举的例子，我们发现$2^3\mathrm{m}\mathrm{o}\mathrm{d}7=1$，也就是说2对7的阶为3，并不是6！

让我们计算一下3对7的阶：
$$\begin{gathered} 3^1\mathrm{m}\mathrm{o}\mathrm{d}7=3 \\ {3}^2\mathrm{m}\mathrm{o}\mathrm{d}7=2 \\ {3}^3\mathrm{m}\mathrm{o}\mathrm{d}7=6 \\ {3}^4\mathrm{m}\mathrm{o}\mathrm{d}7=4 \\ {3}^5\mathrm{m}\mathrm{o}\mathrm{d}7=5 \\ {3}^6\mathrm{m}\mathrm{o}\mathrm{d}7=1 \end{gathered}$$
3的阶是6，也就是说对于7而言，存在一个数3的阶为$\phi (7)$。那么如何称呼满足这种性质的数a呢？我们再给出一个原根的定义：
$$若a,m均为正整数,(a,m)=1,令a^d\mathrm{m}\mathrm{o}\mathrm{d}m=1成立的最小正整数d，其满足d=\phi (m)的话，则称a是模m的原根$$
可以证明，若p是奇质数，则模p的原根存在，而合数就不一定了，例如15就没有原根。

根据上面的推导，选择二元组的要求呼之欲出：在$(g,p)$中，p应当是一个大质数，g应当为p的一个原根，这样一来想要计算出密钥$D_a$是一件相当困难的事情。

生成共同密钥

生成共同密钥的函数$f_2$应当保证两边生成的密钥都是一样的，具体实现为：
$$\begin{gathered} 对于A:S=f_2(D_a,P_b)=P_b^{D_a}\mathrm{m}\mathrm{o}\mathrm{d}p \\ 对于B:S=f_2(D_b,P_a)=P_a^{D_b}\mathrm{m}\mathrm{o}\mathrm{d}p \end{gathered}$$
其中p就是函数$f_1$中的二元组中的p。其实我们把函数$f_1$的参数扩展为两位：$f(D,g)=g^D\mathrm{m}\mathrm{o}\mathrm{d}p$，函数$f_1$和$f_2$的形式是完全一致的。 我们需要证明$f(D_b,f(D_a,g))=f(D_a,f(D_b,g))$成立。以下是证明：

令$t=f(D,g)=g^D\mathrm{m}\mathrm{o}\mathrm{d}p$，则有$g^D=kp+t$，反过来，$t=g^D-kp$，其中k是整数。既然$t=f(D,g)=g^D-kp$，那么有$f(D_a,f(D_b,g))=(t{)}^{D_a}\mathrm{m}\mathrm{o}\mathrm{d}p=(g^{D_b}-kp{)}^{D_a}\mathrm{m}\mathrm{o}\mathrm{d}p$

根据二项式法则展开$(g^{D_b}-kp{)}^{D_a}$，不带有$kp$的项只有一个$g^{D_b{D}_a}$，其他带有$kp$的项计算$\mathrm{m}\mathrm{o}\mathrm{d}p$的结果都为0，因此$$(g^{D_b}-kp{)}^{D_a}\mathrm{m}\mathrm{o}\mathrm{d}p=g^{D_b{D}_a}\mathrm{m}\mathrm{o}\mathrm{d}p$$基于对称性的思想，可以立刻列出$$f(D_b,f(D_a,g))=(g^{D_a}-kp{)}^{D_b}\mathrm{m}\mathrm{o}\mathrm{d}p=g^{D_a{D}_b}\mathrm{m}\mathrm{o}\mathrm{d}p$$所以，$f(D_b,f(D_a,g))=f(D_a,f(D_b,g))$成立。