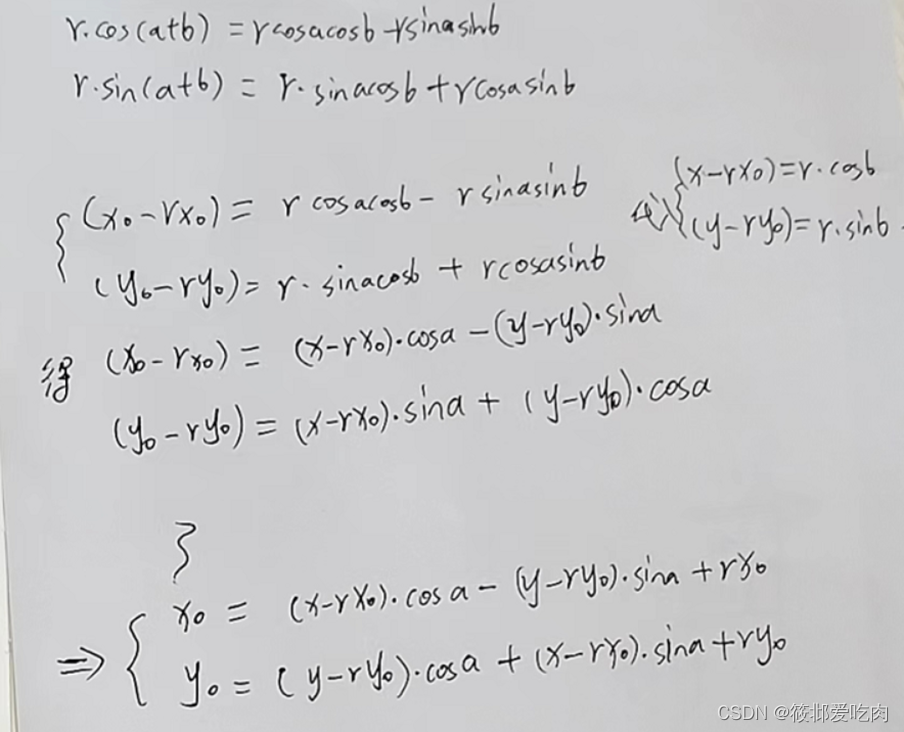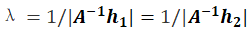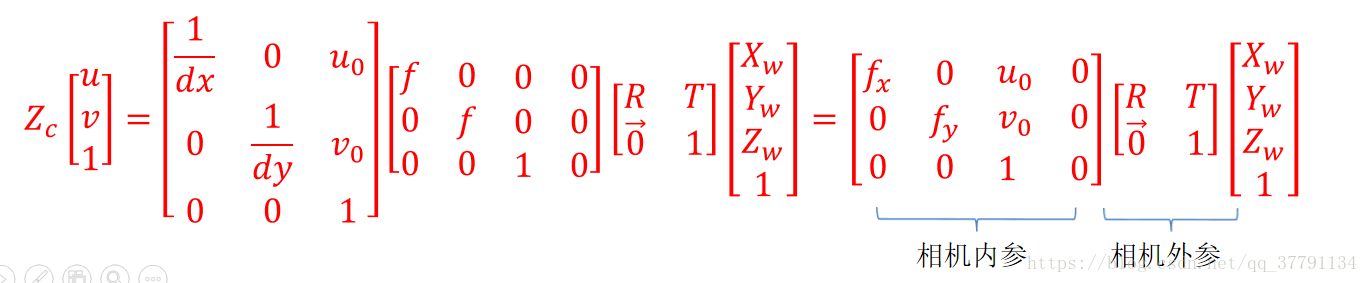相机标定的概念

a. 相机标定的定义

b. 相机标定的目的

相机标定的过程

a. 标定板选择

b. 标定板摆放及拍摄

c. 标定板角点提取

张正友标定法

a. 反解相机矩阵

b.反解畸变系数

使用Python进行相机标定

a. 安装OpenCV

b. 准备标定板图片

c. 利用OpenCV进行角点检测

d. 求解单应矩阵

e. 内外矩阵参数的计算

f. 畸变矫正系数求解

g. 相机标定程序的实现

h. 主函数求解

相机标定的误差

a. 误差来源

b. 误差分析

c. 误差修正

参考文章

相机标定的概念

a. 相机标定的定义

相机标定是指确定相机的内部参数和外部参数的过程。

内部参数包括相机的焦距、像素尺寸、主点位置等；
外部参数包括相机的位置、朝向等。

通过相机标定，可以将像素坐标与实际物理坐标建立对应关系，从而实现机器视觉应用，例如三维重建、姿态估计、目标跟踪等。相机标定的目的是获得准确的相机参数，从而保证图像处理算法的精度和鲁棒性。

b. 相机标定的目的

相机标定的主要目的是获得相机的内部参数和外部参数，建立像素坐标与实际物理坐标之间的对应关系，以实现机器视觉应用。具体来说，相机标定的目的包括以下几个方面：

精确测量：通过相机标定可以精确地测量物体的尺寸、形状、位置和姿态等信息。

三维重建：通过相机标定可以获得三维场景中物体的坐标信息，从而实现三维重建。

目标跟踪：通过相机标定可以将像素坐标与实际物理坐标建立对应关系，实现目标在不同帧之间的跟踪。

机器人导航：通过相机标定可以获取机器人相对于环境的位置和姿态信息，从而实现机器人的导航和控制。

自动化生产：通过相机标定可以实现自动化生产线中的物体检测、计量和分拣等功能。

总之，相机标定的目的是为了准确地获取相机内部参数和外部参数，从而实现机器视觉应用，提高生产效率和产品质量。再直白点就是相机标定的目的是为了获得相机矩阵和畸变系数。

相机标定的过程

a. 标定板选择

在相机标定中，选择合适的标定板是非常重要的。

在尺寸方面，应该根据相机的视场角和最小像素大小来选择，通常标定板至少填满相机视场角的80%；在形状方面有矩形、原型、棋盘格等，这里我们采用的是棋盘格，它可以提供足够的标定点，标定位置也相对于比较容易确定。

b. 标定板摆放及拍摄

标定板的摆放和拍摄过程对相机标定的精度和可靠性有着很大的影响。

在摆放位置上，在相机的视场角内摆放，并要保证标定板的平整度和稳定性，避免标定板出现扭曲、弯曲等情况。同时，标定板应该与相机光轴垂直放置。在拍摄角度上，标定板应该以不同的角度拍摄，包括俯视、仰视、左右侧视等。同时，标定板拍摄时要避免出现阴影和反光等情况，保证标定板表面光滑和均匀。在拍摄数量上，通常情况下，至少需要拍摄10张不同角度和位置的标定板照片来进行相机标定。在拍摄条件上，标定板拍摄时要保证拍摄环境的稳定性，避免光线变化、物体移动等因素对标定结果产生影响。同时，拍摄时要保证相机的曝光、对焦等设置一致。

c. 标定板角点提取

这里我们采用的Python中OpenCV的方法，使用cv2.findChessboardCorners()函数来自动提取标定板的角点。

其技术路线如下所示：

图像预处理：在进行角点提取之前，通常需要对标定板的图像进行预处理，包括灰度化、平滑处理、二值化等。这些处理可以提高角点提取的准确度和稳定性。
标定板参数设置：在使用cv2.findChessboardCorners()函数时，需要设置标定板的参数，包括标定板大小、每行每列的角点数量等。这些参数需要根据实际情况进行设置，以确保角点提取的准确度和稳定性。
角点提取算法选择：OpenCV中提供了多种角点提取算法，包括Harris、Shi-Tomasi、FAST等。在进行相机标定时，通常选择适合于标定板的角点提取算法，以提高角点提取的准确度和稳定性。
角点坐标优化：cv2.findChessboardCorners()函数可以自动提取标定板的角点坐标，但是这些坐标可能存在一定的误差。为了提高标定精度，可以对角点坐标进行优化处理，例如使用cv2.cornerSubPix()函数对角点进行亚像素级别的优化。

所以，在进行标定板角点提取时需要注意预处理、参数设置、算法选择和坐标优化等问题，以确保角点提取的准确度和稳定性。

张正友标定法

张正友标定法是相机标定的经典方法，这里我们从数学的角度来推理它。

a. 反解相机矩阵

在不考虑畸变的情况下，对图像中标定板进行角点检测，得到角点像素坐标值 $[u \quad v \quad 1]^{T}$ ，根据棋盘格的大小，转换到世界坐标系下标定板角点的坐标。

$[^{W}X\quad ^{W}Y\quad ^{W}Z\quad 1]^{T}$

这样我们就可以得到这样的一个式子:

$\left [ \begin {array}{ccc}\hat{u} \\ \hat{v}\\ 1 \end{array}\right ]^{T}=K[^{C}_{W}R \quad ^{C}P_{w_{0}}]\left [ \begin {array}{ccc}^{W}X \\ ^{W}Y\\ ^{W}Z\\1 \end{array}\right ]^{T}$

但为了方便计算，我们常常会让标定板处于 $^{W}Z=0$ ，简单点来说就是将标定板放置在X—Y平面中。

这个式子久简化为了：

$\left [ \begin {array}{ccc}\hat{u} \\ \hat{v}\\ 1 \end{array}\right ]^{T}=K[r_{1}\quad r_{2} \quad p ]\left [ \begin {array}{ccc}^{W}X \\ ^{W}Y\\1 \end{array}\right ]^{T}$

这里的 $r_{1}$ 和 $r_{2}$ 是旋转矩阵 $^{C}_{W}R$ 的前两列，设从标定板到成像平面的单应性矩阵为

$H=\left [ \begin {array}{ccc} h_{11} \quad h_{12} \quad h_{13} \\ h_{21} \quad h_{22} \quad h_{23} \\ h_{31} \quad h_{32} \quad h_{33} \\ \end {array} \right ]= [h_{1} \quad h_{2} \quad h_{3} ]$

$H$ 是一个非奇异3×3矩阵，并且含有比例因子。

基于已知的 $H$ 反解内参数矩阵 $K$ ，代入 $h_{i}=Kr_{i}(i=1,2)$ 可知

$\small \left\{\begin{matrix} h_{1}^{T}Qh_{2}=0\\ h_{1}^{T}Qh_{1}=h_{2}^{T}Qh_{2}=1 \end{matrix}\right.$

其中对称矩阵 $\small Q=K^{-T}K^{-1}$ ，矩阵 $K$ 包含5个元素，需要3组 $H$ 方程可解出 $K$ 的唯一封闭解，因此在标定时需要拍摄三组以上的图片。由 $K$ 可计算出相应的外参矩阵。

$h_{i}^{T}Qh_{j}=[ h_{1} \quad h_{2} \quad h_{3} ]\left [ \begin {array}{ccc} q_{1} \quad q_{2} \quad q_{3} \\ q_{2} \quad q_{4} \quad q_{5} \\ q_{3} \quad q_{4} \quad q_{5} \\ \end {array} \right ]= \left[ \begin {array}{ccc} h_{1} \\ h_{2} \\ h_{3} \end {array} \right ]=v_{ij}^{T}q$

可以改写为

$\left [ \begin {array}{ccc} v_{12}^{T} \\ v_{11}^{T} -v_{22}^{T} \ \end {array} \right ]q=0$

其中矩阵 $V$ 完全由已知的 $H$ 导出， $q$ 为 $Q$ 的向量形式。由于一个 $H$ 最多只能贡献两个线性方程，因此确定内参矩阵至少要3张标定板(工程上一般取10~20张为宜)，这些方程共同构成 $V_{q}=0$ ，使用单应性矩阵估计的归一化直接线性变换解算，解出来就是相机内参矩阵。

上述计算中，忽略了相机畸变的影响（当然这也是最开始给出的条件下），对内外参应用最小二乘法估计实际存在的径向畸变的畸变系数（忽略切向畸变），最后是通过极大似然估计法进行优化，得出较高精度的值。

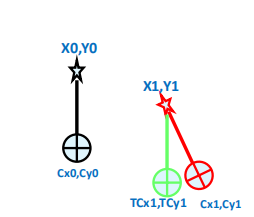
b.反解畸变系数

（张正友标定法只考虑了径向畸变，没有考虑切向畸变）用求得的内参矩阵反解畸变参数。

设：

无畸变像素坐标为 $[\hat{u} \quad \hat{v}]^{T}$
成像平面坐标为 $[\hat{x} \quad \hat{y}]^{T}$
畸变像素坐标为 $[u \quad v]^{T}$
成像平面坐标为 $[x \quad y]^{T}$
内参 $s=0$

则有：

$\begin{cases} u=f_{u}x+c_{u}\\ v=f_{v}y+c_{v} \end{cases}$ $\begin{cases} \hat{u}=f_{u}\hat{x}+c_{u}\\ \hat{v}=f_{v}\hat{y}+c_{v} \end{cases}$

两式相减，并代入 $f_{u}x=u-c_{u}$ 、 $f_{v}y=v-c_{v}$ 以及径向畸变公式

$\begin{cases} \hat{x}=x(1+k_{1}r^{2}+k_{2}r^{4})\\ \hat{y}=y(1+k_{1}r^{2}+k_{2}r^{4}) \end{cases}$

得出

$\left [ \begin {array}{ccc} (u-c_{u})r^{2} \quad (u-c_{u})r^{4}\\ (v-c_{v})r^{2} \quad (v-c_{v})r^{4} \\ \end {array} \right ]\left [ \begin {array}{ccc} k_{1} \\ k_{2} \\ \end {array} \right ]=\left [ \begin {array}{ccc} \hat{u}-u \\ \hat{v}-v \\ \end {array} \right ]$

但由于

$\left [ \begin {array}{ccc}\hat{u} \\ \hat{v}\\ 1 \end{array}\right ]^{T}=K[^{C}_{W}R \quad ^{C}P_{w_{0}}]\left [ \begin {array}{ccc}^{W}X \\ ^{W}Y\\ ^{W}Z\\1 \end{array}\right ]^{T}$

对于 $M$ 幅标定板图片，每张图片取 $N$ 个角点，则可构造非齐次线性方程。

$D_{2MN\times 2}k=d_{2MN\times 1}$

其中 $k=[k_{1}\quad k_{2}]^{T}$ 为畸变系数。最后通过最小二乘法进行回归

$k=(D^{T}D)^{-1}D^{T}d$

使用Python进行相机标定

a. 安装OpenCV

首先需要安装OpenCV库，可以使用pip进行安装：

pip install opencv-python
pip install opencv-contrib-python

b. 准备标定板图片

这一部分是针对没有购买标定板的情况，可以使用代码生成，然后打印拍照。

import cv2
import numpy as np# 定义棋盘格的尺寸
size = 140
# 定义标定板尺寸
boardx = size * 10
boardy = size * 7canvas = np.zeros((boardy, boardx, 1), np.uint8) # 创建画布
for i in range(0, boardx):for j in range(0, boardy):if (int(i/size) + int(j/size)) % 2 != 0: # 判定是否为奇数格canvas[j, i] = 255
cv2.imwrite("chessboard.png", canvas)

这里生成的图片大小为1400*980。如果你想要修改大小，使用ps进行修改是最简单的方法。

c. 利用OpenCV进行角点检测

在进行相机标定时，需要检测标定板上的角点，并将其用于后续的标定计算。OpenCV提供了一个函数 'findChessboardCorners' 来进行角点检测。

下面是一个使用OpenCV进行角点检测的示例代码：

import cv2
import numpy as nppic_name='chessboard.png'
img = cv2.imread(pic_name)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 设置棋盘格尺寸和数量
board_size = (6, 9)
# 找到棋盘格角点
_, corners = cv2.findChessboardCorners(gray, board_size, None)if _:# 提取亚像素角点criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)corners = cv2.cornerSubPix(gray, corners, (11, 11), (-1, -1), criteria)# 在图像上绘制角点img = cv2.drawChessboardCorners(img, board_size, corners, _)cv2.imwrite('corners.png', img)
else:print(f'Unable to find corners in the {pic_name} image.')

这个是单独的一个检测的效果，但在实际拍摄的棋盘格照片中，效果不是很好，暂待改进。

d. 求解单应矩阵

下面的代码是参考了Eating Lee大佬的博客，这里我给出仔细地讲解与分析，尽量保证我是有在这篇博客中添加了自己的东西。

#homography.pyimport numpy as np
from scipy import optimize as opt# 求输入数据的归一化矩阵
def normalizing_input_data(coor_data):x_avg = np.mean(coor_data[:, 0])y_avg = np.mean(coor_data[:, 1])sx = np.sqrt(2) / np.std(coor_data[:, 0])sy = np.sqrt(2) / np.std(coor_data[:, 1])norm_matrix = np.matrix([[sx, 0, -sx * x_avg],[0, sy, -sy * y_avg],[0, 0, 1]])return norm_matrix# 求取初始估计的单应矩阵
def get_initial_H(pic_coor, real_coor):# 获得归一化矩阵pic_norm_mat = normalizing_input_data(pic_coor)real_norm_mat = normalizing_input_data(real_coor)M = []for i in range(len(pic_coor)):# 转换为齐次坐标single_pic_coor = np.array([pic_coor[i][0], pic_coor[i][1], 1])single_real_coor = np.array([real_coor[i][0], real_coor[i][1], 1])# 坐标归一化pic_norm = np.dot(pic_norm_mat, single_pic_coor)real_norm = np.dot(real_norm_mat, single_real_coor)# 构造M矩阵M.append(np.array([-real_norm.item(0), -real_norm.item(1), -1,0, 0, 0,pic_norm.item(0) * real_norm.item(0), pic_norm.item(0) * real_norm.item(1),pic_norm.item(0)]))M.append(np.array([0, 0, 0,-real_norm.item(0), -real_norm.item(1), -1,pic_norm.item(1) * real_norm.item(0), pic_norm.item(1) * real_norm.item(1),pic_norm.item(1)]))# 利用SVD求解M * h = 0中h的解U, S, VT = np.linalg.svd((np.array(M, dtype='float')).reshape((-1, 9)))# 最小的奇异值对应的奇异向量,S求出来按大小排列的，最后的最小H = VT[-1].reshape((3, 3))H = np.dot(np.dot(np.linalg.inv(pic_norm_mat), H), real_norm_mat)H /= H[-1, -1]return H# 返回估计坐标与真实坐标偏差
def value(H, pic_coor, real_coor):Y = np.array([])for i in range(len(real_coor)):single_real_coor = np.array([real_coor[i, 0], real_coor[i, 1], 1])U = np.dot(H.reshape(3, 3), single_real_coor)U /= U[-1]Y = np.append(Y, U[:2])Y_NEW = (pic_coor.reshape(-1) - Y)return Y_NEW# 返回对应jacobian矩阵
def jacobian(H, pic_coor, real_coor):J = []for i in range(len(real_coor)):sx = H[0] * real_coor[i][0] + H[1] * real_coor[i][1] + H[2]sy = H[3] * real_coor[i][0] + H[4] * real_coor[i][1] + H[5]w = H[6] * real_coor[i][0] + H[7] * real_coor[i][1] + H[8]w2 = w * wJ.append(np.array([real_coor[i][0] / w, real_coor[i][1] / w, 1 / w,0, 0, 0,-sx * real_coor[i][0] / w2, -sx * real_coor[i][1] / w2, -sx / w2]))J.append(np.array([0, 0, 0,real_coor[i][0] / w, real_coor[i][1] / w, 1 / w,-sy * real_coor[i][0] / w2, -sy * real_coor[i][1] / w2, -sy / w2]))return np.array(J)# 利用Levenberg Marquart算法微调H
def refine_H(pic_coor, real_coor, initial_H):initial_H = np.array(initial_H)final_H = opt.leastsq(value,initial_H,Dfun=jacobian,args=(pic_coor, real_coor))[0]final_H /= np.array(final_H[-1])return final_H# 返回微调后的H
def get_homography(pic_coor, real_coor):refined_homographies = []error = []for i in range(len(pic_coor)):initial_H = get_initial_H(pic_coor[i], real_coor[i])final_H = refine_H(pic_coor[i], real_coor[i], initial_H)refined_homographies.append(final_H)return np.array(refined_homographies)

实现的是图像配准中的单应性变换求解。

具体来说，实现步骤：

使用归一化矩阵对输入的图像和真实坐标数据进行归一化。
构造M矩阵，并通过SVD求解M * h = 0中h的解。
对估计的单应矩阵进行微调，得到最终的单应矩阵。

对于这一部分，可以结合着上面反解相机矩阵的公式理解。

e. 内外矩阵参数的计算

#InExparam.pyimport numpy as np# 返回每一幅图的外参矩阵[R|t]
def get_ex_param(H, intrinsics_param):ex_param = []inv_intrinsics_param = np.linalg.inv(intrinsics_param)for i in range(len(H)):h0 = (H[i].reshape(3, 3))[:, 0]h1 = (H[i].reshape(3, 3))[:, 1]h2 = (H[i].reshape(3, 3))[:, 2]scale_factor = 1 / np.linalg.norm(np.dot(inv_intrinsics_param, h0))r0 = scale_factor * np.dot(inv_intrinsics_param, h0)r1 = scale_factor * np.dot(inv_intrinsics_param, h1)t = scale_factor * np.dot(inv_intrinsics_param, h2)r2 = np.cross(r0, r1)R = np.array([r0, r1, r2, t]).transpose()ex_param.append(R)return ex_param# 返回pq位置对应的v向量
def create_v(p, q, H):H = H.reshape(3, 3)return np.array([H[0, p] * H[0, q],H[0, p] * H[1, q] + H[1, p] * H[0, q],H[1, p] * H[1, q],H[2, p] * H[0, q] + H[0, p] * H[2, q],H[2, p] * H[1, q] + H[1, p] * H[2, q],H[2, p] * H[2, q]])# 返回相机内参矩阵A
def get_in_param(H):# 构建V矩阵V = np.array([])for i in range(len(H)):V = np.append(V, np.array([create_v(0, 1, H[i]), create_v(0, 0, H[i]) - create_v(1, 1, H[i])]))# 求解V*b = 0中的bU, S, VT = np.linalg.svd((np.array(V, dtype='float')).reshape((-1, 6)))# 最小的奇异值对应的奇异向量,S求出来按大小排列的，最后的最小b = VT[-1]# 求取相机内参w = b[0] * b[2] * b[5] - b[1] * b[1] * b[5] - b[0] * b[4] * b[4] + 2 * b[1] * b[3] * b[4] - b[2] * b[3] * b[3]d = b[0] * b[2] - b[1] * b[1]alpha = np.sqrt(w / (d * b[0]))beta = np.sqrt(w / d ** 2 * b[0])gamma = np.sqrt(w / (d ** 2 * b[0])) * b[1]uc = (b[1] * b[4] - b[2] * b[3]) / dvc = (b[1] * b[3] - b[0] * b[4]) / dreturn np.array([[alpha, gamma, uc],[0, beta, vc],[0, 0, 1]])

get_ex_param实现了从单应矩阵H计算出每张图片的外参矩阵[R|t]，其中R表示旋转矩阵，t表示平移向量。

具体实现流程如下：

首先对相机内参矩阵进行求逆，记为inv_intrinsics_param。

对于每张图片的单应矩阵H，提取出三个列向量h0、h1、h2。

计算缩放因子scale_factor，其计算方法为将inv_intrinsics_param与h0相乘的2范数的倒数。

根据缩放因子计算旋转矩阵R的三列r0、r1、r2，其中r0和r1分别为inv_intrinsics_param与h0、h1相乘并乘以缩放因子，r2通过向量叉积计算得到。

计算平移向量t，其计算方法为inv_intrinsics_param与h2相乘并乘以缩放因子。

将R和t拼接成外参矩阵[R|t]，并将其添加到列表ex_param中。

对于所有的单应矩阵H都完成以上计算后，返回ex_param列表。

create_v给定一个单应性矩阵H和两个点p、q的下标，计算出这两个点在图像上对应的特征向量v。这里的特征向量v是由两个点在图像上的位置关系所决定的，它反映了两个点之间的几何信息，例如旋转、平移、尺度等。

具体来说，这段代码实现了以下步骤：

将H矩阵重构为3x3的形式；

根据p、q的下标计算出特征向量v，其中v是一个6维向量；

将v返回。

get_in_param实现了从多幅图像的单应性矩阵中估计相机的内部参数矩阵A，其中A是一个3x3的矩阵，包含相机的焦距、主点位置和相机的畸变参数等。

主要流程如下：

根据输入的单应矩阵 H ，构建 V 矩阵， V 的大小为 2n 行 6 列，其中 n 为输入单应矩阵 H 的个数。

对 V 进行奇异值分解，得到奇异值矩阵 S 和右奇异向量矩阵 VT 。

取 S 的最后一个奇异值对应的右奇异向量，即 VT 的最后一行，作为 Vb=0 的解 b 。

根据 b 计算相机内参矩阵 A 。

返回相机内参矩阵 A 。

f. 畸变矫正系数求解

#distortion.pyimport numpy as np# 返回畸变矫正系数k0,k1
def get_distortion(intrinsic_param, extrinsic_param, pic_coor, real_coor):D = []d = []for i in range(len(pic_coor)):for j in range(len(pic_coor[i])):# 转换为齐次坐标single_coor = np.array([(real_coor[i])[j, 0], (real_coor[i])[j, 1], 0, 1])# 利用现有内参及外参求出估计图像坐标u = np.dot(np.dot(intrinsic_param, extrinsic_param[i]), single_coor)[u_estim, v_estim] = [u[0] / u[2], u[1] / u[2]]coor_norm = np.dot(extrinsic_param[i], single_coor)coor_norm /= coor_norm[-1]# r = np.linalg.norm((real_coor[i])[j])r = np.linalg.norm(coor_norm)D.append(np.array([(u_estim - intrinsic_param[0, 2]) * r ** 2, (u_estim - intrinsic_param[0, 2]) * r ** 4]))D.append(np.array([(v_estim - intrinsic_param[1, 2]) * r ** 2, (v_estim - intrinsic_param[1, 2]) * r ** 4]))# 求出估计坐标与真实坐标的残差d.append(pic_coor[i][j, 0] - u_estim)d.append(pic_coor[i][j, 1] - v_estim)D = np.array(D)temp = np.dot(np.linalg.inv(np.dot(D.T, D)), D.T)k = np.dot(temp, d)return k

实现了摄像机的畸变矫正，返回畸变矫正系数k0和k1。

具体实现流程如下：

输入摄像机的内参矩阵(intrinsic_param)，外参矩阵(extrinsic_param)，真实的图像坐标(real_coor)和畸变图像坐标(pic_coor)。

对于每一个真实坐标(real_coor[i])[j]，将其转换为齐次坐标并利用内参矩阵和外参矩阵求出估计图像坐标(u_estim, v_estim)。

根据真实坐标的归一化坐标(coor_norm)计算半径r，并利用估计图像坐标和内参矩阵计算畸变系数D，并将其存入D数组中。

计算估计坐标与真实坐标的残差，并将其存入d数组中。

将D数组和d数组用最小二乘法求出畸变矫正系数k0和k1，返回结果。

g. 相机标定程序的实现

#refine_all.pyimport numpy as np
import math
from scipy import optimize as opt# 微调所有参数
def refinall_all_param(A, k, W, real_coor, pic_coor):# 整合参数P_init = compose_paramter_vector(A, k, W)# 复制一份真实坐标X_double = np.zeros((2 * len(real_coor) * len(real_coor[0]), 3))Y = np.zeros((2 * len(real_coor) * len(real_coor[0])))M = len(real_coor)N = len(real_coor[0])for i in range(M):for j in range(N):X_double[(i * N + j) * 2] = (real_coor[i])[j]X_double[(i * N + j) * 2 + 1] = (real_coor[i])[j]Y[(i * N + j) * 2] = (pic_coor[i])[j, 0]Y[(i * N + j) * 2 + 1] = (pic_coor[i])[j, 1]# 微调所有参数P = opt.leastsq(value,P_init,args=(W, real_coor, pic_coor),Dfun=jacobian)[0]# raial_error表示利用标定后的参数计算得到的图像坐标与真实图像坐标点的平均像素距离error = value(P, W, real_coor, pic_coor)raial_error = [np.sqrt(error[2 * i] ** 2 + error[2 * i + 1] ** 2) for i in range(len(error) // 2)]print("total max error:\t", np.max(raial_error))# 返回拆解后参数，分别为内参矩阵，畸变矫正系数，每幅图对应外参矩阵return decompose_paramter_vector(P)# 把所有参数整合到一个数组内
def compose_paramter_vector(A, k, W):alpha = np.array([A[0, 0], A[1, 1], A[0, 1], A[0, 2], A[1, 2], k[0], k[1]])P = alphafor i in range(len(W)):R, t = (W[i])[:, :3], (W[i])[:, 3]# 旋转矩阵转换为一维向量形式zrou = to_rodrigues_vector(R)w = np.append(zrou, t)P = np.append(P, w)return P# 分解参数集合，得到对应的内参，外参，畸变矫正系数
def decompose_paramter_vector(P):[alpha, beta, gamma, uc, vc, k0, k1] = P[0:7]A = np.array([[alpha, gamma, uc],[0, beta, vc],[0, 0, 1]])k = np.array([k0, k1])W = []M = (len(P) - 7) // 6for i in range(M):m = 7 + 6 * izrou = P[m:m + 3]t = (P[m + 3:m + 6]).reshape(3, -1)# 将旋转矩阵一维向量形式还原为矩阵形式R = to_rotation_matrix(zrou)# 依次拼接每幅图的外参w = np.concatenate((R, t), axis=1)W.append(w)W = np.array(W)return A, k, W# 返回从真实世界坐标映射的图像坐标
def get_single_project_coor(A, W, k, coor):single_coor = np.array([coor[0], coor[1], coor[2], 1])# '''coor_norm = np.dot(W, single_coor)coor_norm /= coor_norm[-1]# r = np.linalg.norm(coor)r = np.linalg.norm(coor_norm)uv = np.dot(np.dot(A, W), single_coor)uv /= uv[-1]# 畸变u0 = uv[0]v0 = uv[1]uc = A[0, 2]vc = A[1, 2]# u = (uc * r**2 * k[0] + uc * r**4 * k[1] - u0) / (r**2 * k[0] + r**4 * k[1] - 1)# v = (vc * r**2 * k[0] + vc * r**4 * k[1] - v0) / (r**2 * k[0] + r**4 * k[1] - 1)u = u0 + (u0 - uc) * r ** 2 * k[0] + (u0 - uc) * r ** 4 * k[1]v = v0 + (v0 - vc) * r ** 2 * k[0] + (v0 - vc) * r ** 4 * k[1]'''uv = np.dot(W, single_coor)uv /= uv[-1]# 透镜矫正x0 = uv[0]y0 = uv[1]r = np.linalg.norm(np.array([x0, y0]))k0 = 0k1 = 0x = x0 * (1 + r ** 2 * k0 + r ** 4 * k1)y = y0 * (1 + r ** 2 * k0 + r ** 4 * k1)#u = A[0, 0] * x + A[0, 2]#v = A[1, 1] * y + A[1, 2][u, v, _] = np.dot(A, np.array([x, y, 1]))'''return np.array([u, v])# 返回所有点的真实世界坐标映射到的图像坐标与真实图像坐标的残差
def value(P, org_W, X, Y_real):M = (len(P) - 7) // 6N = len(X[0])A = np.array([[P[0], P[2], P[3]],[0, P[1], P[4]],[0, 0, 1]])Y = np.array([])for i in range(M):m = 7 + 6 * i# 取出当前图像对应的外参w = P[m:m + 6]# 不用旋转矩阵的变换是因为会有精度损失'''R = to_rotation_matrix(w[:3])t = w[3:].reshape(3, 1)W = np.concatenate((R, t), axis=1)'''W = org_W[i]# 计算每幅图的坐标残差for j in range(N):Y = np.append(Y, get_single_project_coor(A, W, np.array([P[5], P[6]]), (X[i])[j]))error_Y = np.array(Y_real).reshape(-1) - Yreturn error_Y# 计算对应jacobian矩阵
def jacobian(P, WW, X, Y_real):M = (len(P) - 7) // 6N = len(X[0])K = len(P)A = np.array([[P[0], P[2], P[3]],[0, P[1], P[4]],[0, 0, 1]])res = np.array([])for i in range(M):m = 7 + 6 * iw = P[m:m + 6]R = to_rotation_matrix(w[:3])t = w[3:].reshape(3, 1)W = np.concatenate((R, t), axis=1)for j in range(N):res = np.append(res, get_single_project_coor(A, W, np.array([P[5], P[6]]), (X[i])[j]))# 求得x, y方向对P[k]的偏导J = np.zeros((K, 2 * M * N))for k in range(K):J[k] = np.gradient(res, P[k])return J.T# 将旋转矩阵分解为一个向量并返回，Rodrigues旋转向量与矩阵的变换,最后计算坐标时并未用到，因为会有精度损失
def to_rodrigues_vector(R):p = 0.5 * np.array([[R[2, 1] - R[1, 2]],[R[0, 2] - R[2, 0]],[R[1, 0] - R[0, 1]]])c = 0.5 * (np.trace(R) - 1)if np.linalg.norm(p) == 0:if c == 1:zrou = np.array([0, 0, 0])elif c == -1:R_plus = R + np.eye(3, dtype='float')norm_array = np.array([np.linalg.norm(R_plus[:, 0]),np.linalg.norm(R_plus[:, 1]),np.linalg.norm(R_plus[:, 2])])v = R_plus[:, np.where(norm_array == max(norm_array))]u = v / np.linalg.norm(v)if u[0] < 0 or (u[0] == 0 and u[1] < 0) or (u[0] == u[1] and u[0] == 0 and u[2] < 0):u = -uzrou = math.pi * uelse:zrou = []else:u = p / np.linalg.norm(p)theata = math.atan2(np.linalg.norm(p), c)zrou = theata * ureturn zrou# 把旋转矩阵的一维向量形式还原为旋转矩阵并返回
def to_rotation_matrix(zrou):theta = np.linalg.norm(zrou)zrou_prime = zrou / thetaW = np.array([[0, -zrou_prime[2], zrou_prime[1]],[zrou_prime[2], 0, -zrou_prime[0]],[-zrou_prime[1], zrou_prime[0], 0]])R = np.eye(3, dtype='float') + W * math.sin(theta) + np.dot(W, W) * (1 - math.cos(theta))return R

标定相机的目的是确定相机内参（包括焦距、像素间距、主点坐标等参数）和畸变参数（包括径向畸变和切向畸变），以便将从相机拍摄得到的图像坐标转换为真实世界坐标。

具体实现过程为：根据给定的真实世界坐标和对应的图像坐标，使用最小二乘法，通过优化算法求解相机内参、畸变参数和每幅图像的外参，得到最优的相机标定参数。其中，相机内参和畸变参数是所有图像共享的，而每幅图像的外参是单独计算的。

该程序实现了以下几个函数：

refinall_all_param：微调所有参数
compose_paramter_vector：把所有参数整合到一个数组内
decompose_paramter_vector：分解参数集合，得到对应的内参、外参和畸变矫正系数
get_single_project_coor：根据相机内参、畸变参数和外参，返回从真实世界坐标映射的图像坐标

h. 主函数求解

import cv2
import numpy as np
import osfrom parameter.homography import get_homography
from parameter.InExparam import get_ex_param,get_in_param
from parameter.distortion import get_distortion
from parameter.refine_all import refinall_all_paramdef calibrate():# 求单应矩阵H = get_homography(pic_points, real_points_x_y)# 求内参intrinsics_param = get_in_param(H)# 求对应每幅图外参extrinsics_param = get_ex_param(H, intrinsics_param)# 畸变矫正k = get_distortion(intrinsics_param, extrinsics_param, pic_points, real_points_x_y)# 微调所有参数[new_intrinsics_param, new_k, new_extrinsics_param] = refinall_all_param(intrinsics_param,k, extrinsics_param, real_points,pic_points)print("intrinsics_parm:\t", new_intrinsics_param)print("distortionk:\t", new_k)print("extrinsics_parm:\t", new_extrinsics_param)if __name__ == "__main__":file_dir = r'E:\pythonconda2\demarcate\calibration_pic'# 标定所用图像pic_name = os.listdir(file_dir)# 由于棋盘为二维平面，设定世界坐标系在棋盘上，一个单位代表一个棋盘宽度，产生世界坐标系三维坐标cross_corners = [7, 4]  # 棋盘方块交界点排列real_coor = np.zeros((cross_corners[0] * cross_corners[1], 3), np.float32)real_coor[:, :2] = np.mgrid[0:7, 0:4].T.reshape(-1, 2)real_points = []real_points_x_y = []pic_points = []for pic in pic_name:pic_path = os.path.join(file_dir, pic)pic_data = cv2.imread(pic_path)# 寻找到棋盘角点succ, pic_coor = cv2.findChessboardCorners(pic_data, (cross_corners[0], cross_corners[1]), None)if succ:# 添加每幅图的对应3D-2D坐标pic_coor = pic_coor.reshape(-1, 2)pic_points.append(pic_coor)real_points.append(real_coor)real_points_x_y.append(real_coor[:, :2])calibrate()

通过标定一组摄像机的内部参数（包括焦距、主点等）和外部参数（包括相机在空间中的位置和方向等），使得摄像机拍摄的图像能够准确地反映出真实场景的几何信息。具体实现中，程序通过找到棋盘格的角点来建立图像和真实场景之间的对应关系，并使用多个图像中的对应点来计算摄像机的内部和外部参数，同时还进行了畸变校正和参数微调等处理。

具体的流程按如下进行：

定义标定所需的文件夹路径和棋盘格角点排列方式。
创建一个3D的世界坐标系，设定每个方格的大小，生成对应的坐标。
遍历标定所用的图片文件夹，读取每一幅图像。
对于每幅图像，通过OpenCV中的findChessboardCorners函数寻找棋盘格角点，并将其存储在 pic_points 数组中。
将世界坐标系的3D坐标存储在 real_points 数组中。
将世界坐标系的x和y坐标存储在 real_points_x_y 数组中。
调用函数 calibrate() 进行标定，该函数的实现流程如下：

通过findChessboardCorners函数获取所有图片的角点坐标和对应的世界坐标系的3D坐标。
使用get_homography函数获取所有图片的单应矩阵H。
使用get_in_param函数求解内参。
使用get_ex_param函数求解每幅图像的外参。
使用get_distortion函数对图片进行畸变矫正。
使用refinall_all_param函数对内参、畸变参数和外参进行微调。
输出标定结果的内参、畸变参数和外参。