选择排序：

基本思想：

每一趟从待排序数组中选出最小的数字，按顺序放在已经排好序的数组的后面，直到全部排完。

1：简单选择排序：

基本思想：

每次选出最小的数，放在已排好数组最后。

过程：

示意图如下：

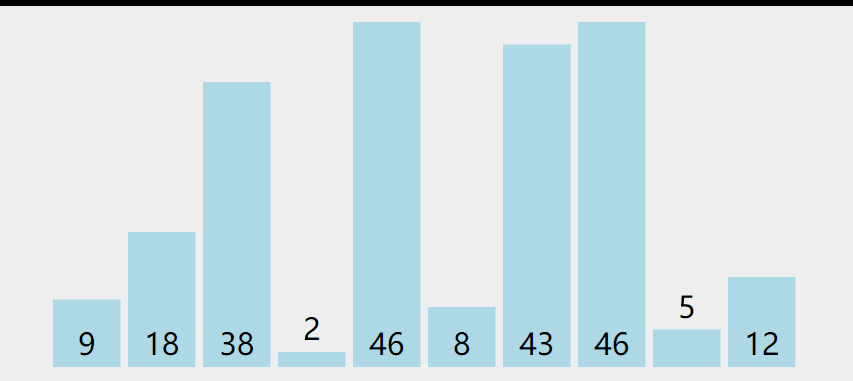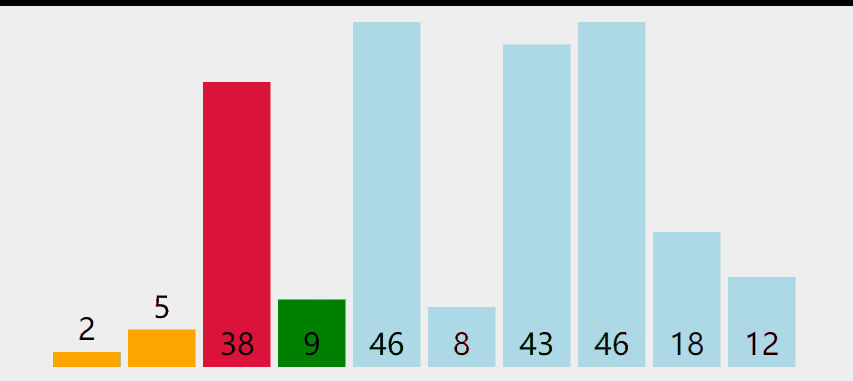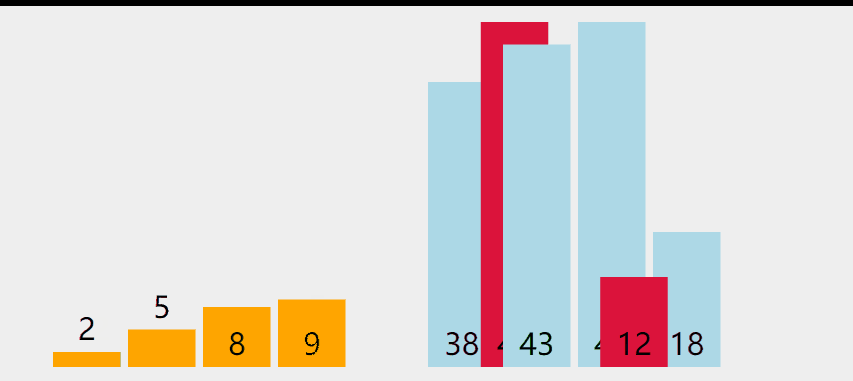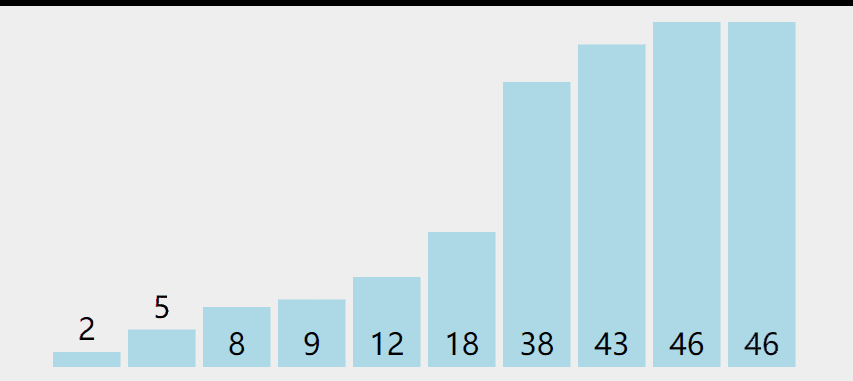
代码实现：

import java.util.Arrays;public class SimpleSelectSort {public static void main(String[] args) {int[] a={3,1,1,2,4,4,7};SelectSort2(a);System.out.println(Arrays.toString(a));}//不稳定版(常规版本)private static void SelectSort(int[] s){for(int i=0;i<s.length;i++){int k=i;//指向第一个数for (int j=i+1;j<s.length;j++){if (s[j]<s[k]){//如果有小于k所指向的数k=j;//则将该数的下标赋值给k}}if (k!=i){//如果k值发生改变，就交换[k]与[i]int temp=s[k];s[k]=s[i];s[i]=temp;}}}//辅助数组版private static void SelectSort1(int[] s){double[] temp=new double[s.length];//辅助数组tempfor (int i=0;i<s.length;i++){//把s里的值赋给temptemp[i]=s[i];}for (int i=0;i<temp.length;i++){int k=i;for (int j=0;j<temp.length;j++){if (temp[j]<temp[k]){k=j;//得到最小数}}s[i]=(int)temp[k];//赋给s的第i个位置temp[k]=1.0/0;//赋值为正无穷大}}//稳定版private static void SelectSort2(int[] s){for(int i=0;i<s.length;i++){int k=i;//指向第一个数for (int j=i+1;j<s.length;j++){if (s[j]<s[k]){//如果有小于k所指向的数k=j;//则将该数的下标赋值给k}}if (k!=i){//如果k值发生改变，将k之前的数前移一位，再把[k]赋给[i]int temp=s[k];for (int y=i;y<k;y++){s[y+1]=s[y];}s[i]=temp;}}}}

给出了三个版本，结果算出来都一样。

结果：

时间复杂度： $O(n^{2})$

空间复杂度： $O(1)$ (常规)

算法特点：

（1）:不稳定排序。（也有稳定版）

（2）:移动次数较少，当每一个数占用空间较多时，比直接插入排序快

2：堆排序：

基本思想：

利用完全二叉树的顺序存储结构，及完全二叉树中双亲结点和孩子之间的关系，在当前无序数组中选择最大数(或最小数)。（也就是利用大根堆或小根堆）

每个结点的值都大于其左孩子和右孩子结点的值，称之为大根堆。

每个结点的值都小于其左孩子和右孩子结点的值，称之为小根堆。

父结点索引：(i-1)/2

左孩子索引：2*i+1

右孩子索引：2*i+2

过程：

过程演示连接

代码实现：

import java.util.Arrays;public class HeapSort {public static void main(String[] args) {int[] a={3,1,1,2,4,4,7};Sort(a);System.out.println(Arrays.toString(a));}private static void Sort(int[] s){//第一次将原数组建立成大根堆(每个结点的值都大于其左孩子和右孩子结点的值，称之为大根堆)for (int i=(s.length-1-1)/2;i>=0;i--){//父节点为(i-1)/2，i为数组下标CreateHeap(s,i,s.length-1);//从下往上构建}for (int j=s.length-1;j>0;j--){//将堆顶[0](也就是最大值)放在[j](也就是数组最后)int temp=s[0];s[0]=s[j];s[j]=temp;//将数组下标的0到j-1重新调整为大根堆CreateHeap(s,0,j-1);}}private static void CreateHeap(int[] s,int a,int b){int temp=s[a];//2a+1为左孩子，2a+2为右孩子for(int i=2*a+1;i<=b;i=i*2+1){if (i<b&&s[i]<s[i+1]){//存在右孩子且右孩子大于左孩子i++;//让i指向大的孩子，也就是右孩子}if(s[i]>temp){//大的孩子如果大于第一个数s[a]=s[i];//大孩子上位父节点a=i;//将a锁定为大值的下标}else {//左右孩子都不大于父节点，说明已经成为大根堆，直接跳出循环break;}}s[a]=temp;//将第一个数赋给最终的大值的位置}}

结果：