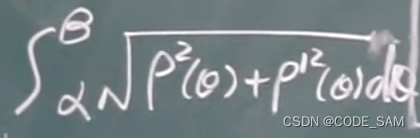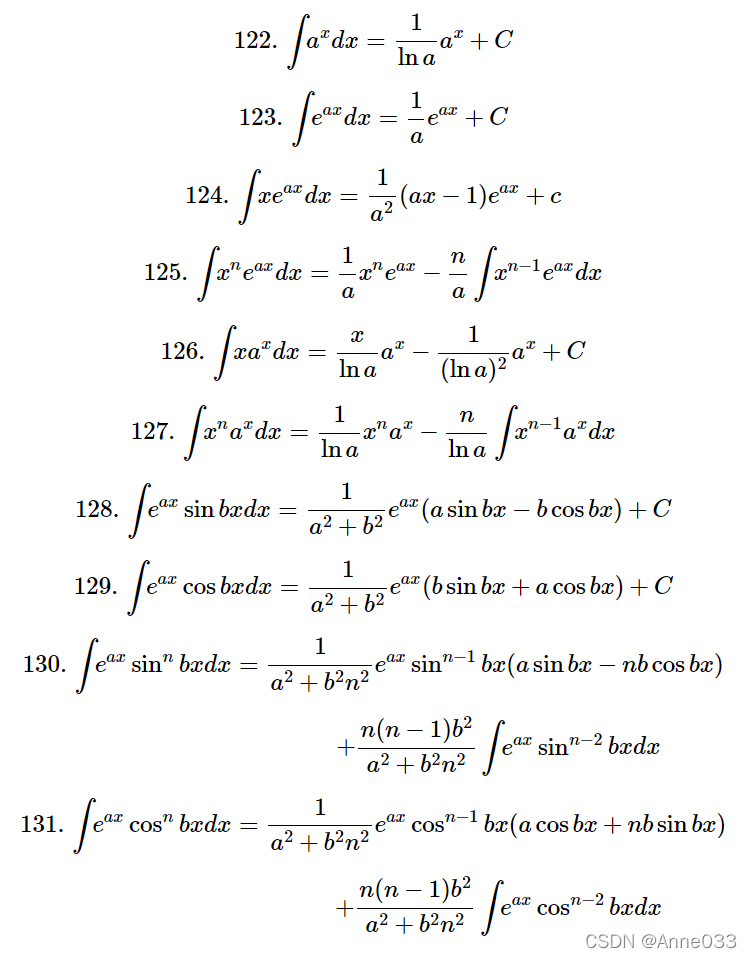【数学-常用公式】基本积分表

article/2025/9/1 10:03:30

【基本积分表】 

    1) \int dx = x + C                                               2)\int kdx = kx + C(k \neq 0)

    3) \int x^{\mu } dx = \frac {x^{\mu + 1}}{\mu + 1} + C (\mu \neq -1)                    4)\int \frac {dx}{x} = ln \left | x \right | + C (x \neq 0)

    5) \int \frac {dx}{1 + x^2} = arctan x + C                             6)\int \frac {dx}{\sqrt {1 - x^{2}}} = arcsin x + C

    7) \int cos x dx = sin x + C                                   8) \int sin x dx = - cos x + C

    9) \int \frac {dx}{cos^{2}x} = \int sec^{2}dx = tan x + C               10)\int \frac {dx}{sin^{2}x} = \int csc^{2}dx = -cot + C

    11) \int sec x tan x dx = sec x + C                         12)\int csc x cot x dx = -csc x + C

    13)\int e^{x}dx = e^{x} + C                                         14)\int a^{x}dx = \frac {a^{x}}{lna} + C (a >0, a \neq 1)

    15)\int shx dx = ch x + C                                    16)\int ch x dx = sh x + C

【基本积分表的扩充】 

    17) \int tan x dx = -ln \left| cos x \right| + C                       18) \int cot x dx = ln \left| sin x \right| + C

    19) \int sec x dx = ln \left| sec x + tan x \right| + C              20) \int csc x dx = ln \left| csc x - cot x \right| + C = ln \left| tan \frac{x}{2} \right| + C

    21)\int \frac{dx}{a^{2} + x^{2}} = \frac {1}{a}arctan \frac {x}{a} + C                      22)\int \frac {dx}{x^{2} - a^{2}} = \frac {1}{2a}ln \left| \frac {x - a}{x + a} \right| + C

    23)\int \frac {dx}{a^{2} - x^{2}} = \frac{1}{2a}ln \left| \frac {a + x}{a - x} \right| + C                 24)\int \frac {dx}{\sqrt {a^{2} - x^{2}}} = arcsin \frac {x}{a} + C

    25)\int \frac {dx}{\sqrt {x^{2} + a^{2}}} = ln(x + \sqrt {x^{2} + a^{2}}) + C       26)\int \frac {dx}{\sqrt {x^{2} - a^{2}}} = ln \left| x + \sqrt {x^{2} - a^{2}} \right| + C

 

注：来自《高等数学》（第五版）上册 同济大学数学系

 

 


http://chatgpt.dhexx.cn/article/M9kPpmCD.shtml

相关文章

【数学】定积分计算

【数学】定积分计算

目录 1.定义2.定理与性质2.1积分上限函数2.2积分中值定理2.3其它性质与定理 3.做题技巧、题型 1.定义 i f lim ⁡ x → λ ∑ i 1 n f ( ξ i ) △ x i ∃ ， 则 f ( x ) 在 [ a , b ] 上 可 积 if \lim_{x \to \lambda} \sum_{i1}^n f(\xi_i)△x_i \exists&#x…
阅读更多...
高数：定积分

高数：定积分

引入&#xff1a;曲边梯形面积 a和b中两点插入n个点&#xff0c;ax0<x1<x2...xnb&#xff0c;产生n-1个小片段x1-x0&#xff0c; x2-x1...... 取n个区间内某点的函数值&#xff0c;y0&#xff0c;y1&#xff0c;y2...yn 产生多个小长方形面积&#xff0c;sx*y 取为x1…
阅读更多...
必记的13个不定积分公式(详细推导)

必记的13个不定积分公式(详细推导)

常见积分公式 前言1 ∫ c s c x d x l n ∣ c s c x − c o t x ∣ C \int cscxdxln|cscx-cotx|C ∫cscxdxln∣cscx−cotx∣C2 ∫ s e c x d x l n ∣ s e c x t a n x ∣ C \int secxdxln|secxtanx|C ∫secxdxln∣secxtanx∣C3 ∫ d x x 2 − a 2 l n ∣ x x 2 − a…
阅读更多...
高数-定积分-公式

高数-定积分-公式

阅读更多...
微分和积分数学公式大全

微分和积分数学公式大全

一、极限公式 &#xff08;系数不为0的情况&#xff09; 二、重要公式 三、下列常用等价无穷小关系&#xff08;x->0&#xff09; 四、导数的四则运算法则 五、基本导数公式 六、高阶导数的运算法则 七、基本初等函数的n阶导数公式 八、微分公式与微分运算法则 九、微分运算…
阅读更多...
微积分常用公式

微积分常用公式

一、基本导数公式 二、导数的四则运算法则 三、高阶导数的运算法则 四、基本初等函数的n阶导数公式 五、微分公式与微分运算法则 六、微分运算法则 七、基本积分公式 八、补充积分公式 九、下列常用凑微分公式 十、分部积分法公式 十一、第二换元积分法中的三角换元公式…
阅读更多...
微分和积分公式大全

微分和积分公式大全

1 极限公式 &#xff08;系数不为0的情况&#xff09; 2 下列常用等价无穷小关系&#xff08;x->0&#xff09; 3 导数的四则运算法则 4 基本导数公式 5 高阶导数的运算法则 6 基本初等函数的n阶导数公式 7 微分公式与微分运算法则 8 微分运算法则 9 基本积分公式 10 下…
阅读更多...
微积分公式大全

微积分公式大全

PDF下载地址&#xff1a; http://pan.baidu.com/s/1i5kl3CD
阅读更多...
积分公式大全

积分公式大全

https://kexue.fm/sci/integral/ 《积分公式大全》网络版本——By BoJone 引用原作者的话&#xff1a; 本附件所有公式来自《高等数学第三版》。 　　该书信息&#xff1a;同济大学数学教研室编&#xff0c;高等教育出版社&#xff0c;1988年4月第三版&#xff0c;ISBN 7-04-0…
阅读更多...
高等数学积分公式大全

高等数学积分公式大全

高等数学积分公式大全 导数公式&#xff1a; 基本积分表&#xff1a; 三角函数的有理式积分&#xff1a; 曲率&#xff1a; 更多参见&#xff1a; http://wenku.baidu.com/view/983d572a915f804d2a16c104.html http://wenku.baidu.com/view/19a66aeef8c75fbfc77db2bf.html http…
阅读更多...
不定积分公式 定积分公式

不定积分公式 定积分公式

不定积分基本公式 第一换元法 将函数换变成自变量 第二换元法 将自变量变成函数 常用定积分公式
阅读更多...
5.2 积分基本公式

5.2 积分基本公式

在上一节中&#xff0c;我们总结了定积分的概念和性质&#xff0c;定积分的定义如下 但是我就觉得吧&#xff0c;这个定义它看着都费劲&#xff0c;让我用它计算去解决问题&#xff1f;你杀我吧。实在是因为用定义的方式计算定积分不是一件容易的事情。 所以本篇内容就来搞一个…
阅读更多...
spring源码学习之整合Mybatis原理分析

spring源码学习之整合Mybatis原理分析

本文主要解析spring是如何与mybatis进行整合&#xff0c;整合的过程中需要哪些组件的支持。以前面提到过的配置例子《spring源码学习之aop事物标签解析》 整合的过程中需要使用以下这个依赖包&#xff1a; <!-- mybatis-spring 整合 --> <dependency><groupId…
阅读更多...
MyBatis架构原理详解

MyBatis架构原理详解

1. Mybatis架构设计 MyBatis 是 Java 生态中非常著名的一款 ORM 框架&#xff0c;目前在一线互联网大厂中应用广泛&#xff0c;Mybatis已经成为了一个必会框架。 Mybatis的功能架构分为三层&#xff1a; API接口层数据处理层基础支撑层 2. API接口层 接口层&#xff1a;主要…
阅读更多...
springboot集成mybatis原理剖析

springboot集成mybatis原理剖析

前言&#xff1a;本文主要基于springboot项目&#xff0c;从springboot的拓展角度来分析mybatis是如何与springboot集成的。 1、首先搭建springboot集成mybatis环境 1.1、maven pom文件依赖 <?xml version"1.0" encoding"UTF-8"?> <project x…
阅读更多...
MyBatis原理分析（通俗易懂）

MyBatis原理分析（通俗易懂）

MyBatis原理分析 MyBatis工作流程简述原生MyBatis原理分析初始化工作解析配置文件配置类方式 执行SQLSqlSession API方式接口方式 真正掌握一个框架源码分析是少不了的~ 在讲解整合Spring的原理之前理解原生的MyBatis执行原理是非常有必要的 MyBatis工作流程简述 传统工作模…
阅读更多...
【MyBatis学习笔记九】——MyBatis原理

【MyBatis学习笔记九】——MyBatis原理

一、Mybatis工作原理图 mybatis 原理图如下所示&#xff1a; 二、工作原理解析 mybatis应用程序通过SqlSessionFactoryBuilder从mybatis-config.xml配置文件&#xff08;也可以用Java文件配置的方式&#xff0c;需要添加Configuration&#xff09;来构建SqlSessionFactory&…
阅读更多...
【mybatis原理工作原理】

【mybatis原理工作原理】

文章目录 mybatis原理&#xff1a;mybatis缓存机制 mybatis原理&#xff1a; mybatis的工作原理就是&#xff1a;先封装sql&#xff0c;接着调用jdbc操作数据库&#xff0c;最后把数据库返回的表结果封装成java类。 通过代码实现jdbc查询操作&#xff1a; mybatis-config.xm…
阅读更多...
mybatis原理(含图)

mybatis原理(含图)

上面中流程就是MyBatis内部核心流程&#xff0c;每一步流程的详细说明如下文所述&#xff1a; &#xff08;1&#xff09;读取MyBatis的配置文件。mybatis-config.xml为MyBatis的全局配置文件&#xff0c;用于配置数据库连接信息。 &#xff08;2&#xff09;加载映射文件。映…
阅读更多...
MyBatis原理分析

MyBatis原理分析

是什么? MyBatis 是一款优秀的持久层框架&#xff0c;它支持定制化 SQL、存储过程以及高级映射。MyBatis 避免了几乎所有的 JDBC 代码和手动设置参数以及获取结果集。MyBatis可以使用简单的 XML 或注解来配置和映射原生类型、接口和 Java 的 POJO&#xff08;Plain Old Java …
阅读更多...
推荐文章

Copyright @ 2022~2023