SplitChunksPlugin
SplitChunks是Webpack中一个提取或分离代码的插件,主要作用是提取公共代码,防止代码被重复打包,拆分过大的js文件,合并零散的js文件。
推荐网址:https://webpack.docschina.org/plugins/split-chunks-plugin/
webpack其他相关给、推荐
一:webpack优化相关
1:webpack优化系列一:webpack不同环境打包配置
2:webpack优化系列二:Vue配置compression-webpack-plugin实现Gzip压缩
3:webpack优化系列三:vue子目录路径更改—publicPath
4:webpack优化系列四:vue打包后生成的chunk-vendors文件过大,利用SplitChunks插件,分离chunk
demo:vue.config.js中相关配置
const ISPROD = process.env.NODE_ENV === 'production'
module.exports = {chainWebpack(config) {if (ISPROD) {config.optimization.splitChunks({cacheGroups: {common: {//commons 一般是是个人定义的name: 'chunk-common', // 打包后的文件名chunks: 'initial',minChunks: 1,maxInitialRequests: 5,minSize: 0,priority: 1,reuseExistingChunk: true},vendors: {//vendor 是导入的 npm 包name: 'chunk-vendors',test: /[\\/]node_modules[\\/]/,chunks: 'initial',maxSize: 600000,maxInitialRequests: 20,priority: 2,reuseExistingChunk: true,enforce: true},antDesignVue: {//把antDesignVue从chunk-vendors.js提取出来。当然我们也可以把mixins,vue.min.js等等也按照类似配置提取出来name: 'chunk-ant-design-vue',test: /[\\/]node_modules[\\/]ant-design-vue[\\/]/,chunks: 'initial',priority: 3,maxSize: 600000,reuseExistingChunk: true,enforce: true}}})}}
}
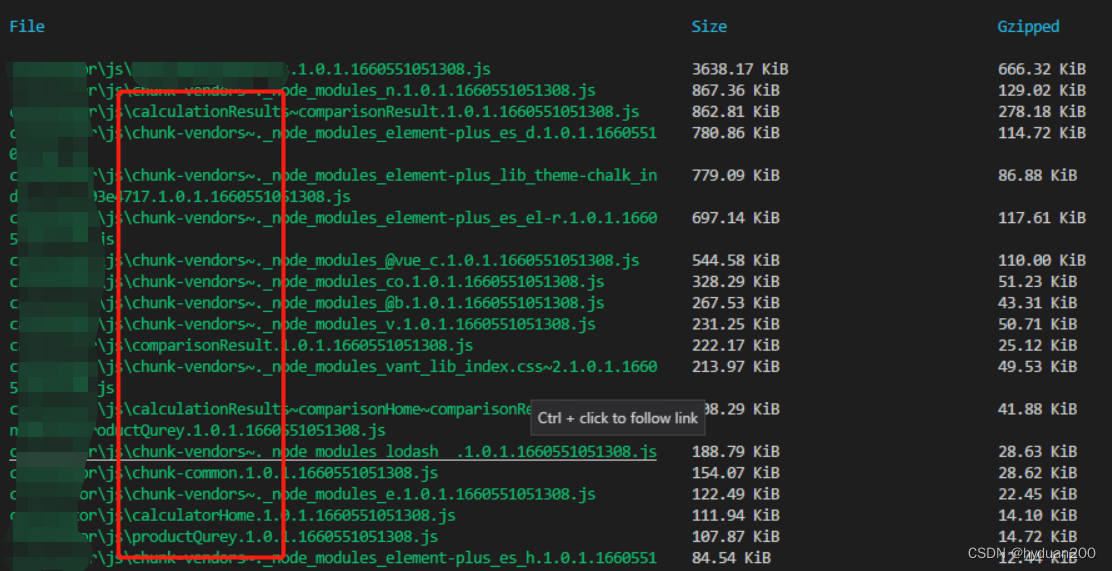
未使用前效果

使用后效果