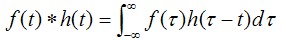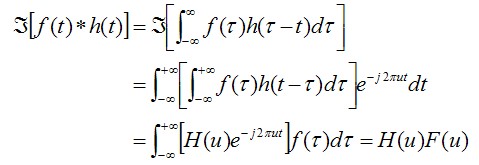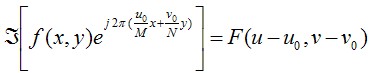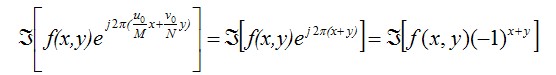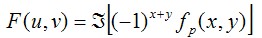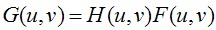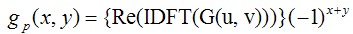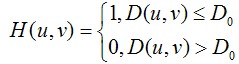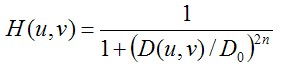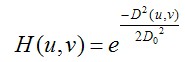1.傅里叶变换与频域
在之前的文中,我们已经进行过一些基本的图像处理。比如,使用低通滤波可以将图像模糊,也有些许降噪的作用。这些都是在空间域内进行的滤波处理,这个处理主要是依靠卷积来进行计算的。首先,从连续的一维卷积入手,如下所示。
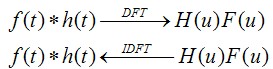
将上式进行傅里叶变换,可以得到如下结果。
从这个式子,我们可以得到一个重要的结论。也就是,函数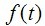
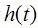
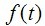
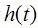
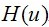
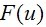
在将其扩展到二维的形况下,假设尺寸为MxN的图像,如下关系是成立的。
其实到这,基本的原理就明了的。我们所看到的图像,均为空间域内的表现形式,我们无法辨识出频域内的图像。要进行频域内的滤波器处理,首先就需要进行傅里叶变换,然后直接进行滤波处理,最后再用反傅里叶变换倒回到空间域内。
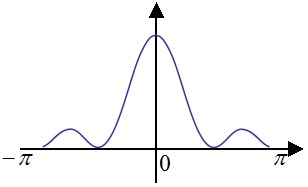
到此,已经可以开始空间域内的滤波处理了。但是,还有一点需要注意的地方。使用某个一维信号来举例子,一维信号的傅里叶变换是以2π为周期的函数。所以,我们常常使用的范围[-π,π]来表示这个信号的傅里叶变换,如下所示。
这样做的好处是,靠近0的成分就是低频,靠近-π与π的成分就表示高频。而对于图像而言,在Matlab中,我们使用fft2()这个函数来求取图像的傅里叶变换。
[plain] view plain copy

 正在上传…重新上传取消
正在上传…重新上传取消![]()
 正在上传…重新上传取消
正在上传…重新上传取消
- g = fft2(f);
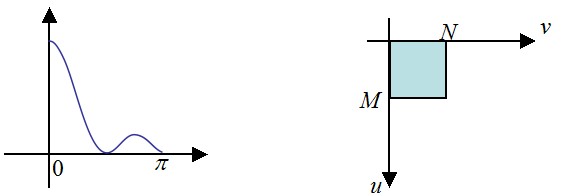
上面这个代码求取的,其实是范围[0,π]内的傅里叶变换。为了方便理解,下图画出了本行代码所求取的图像的傅里叶变换的范围(右)和与其等效的一维傅里叶变换的范围(左)。
很显然,这并不是希望的范围,下面这个代码可以求取[0,2π]内的傅里叶变换。
[plain] view plain copy

 正在上传…重新上传取消
正在上传…重新上传取消![]()
 正在上传…重新上传取消
正在上传…重新上传取消
- P = 2*M;
- Q = 2*N;
- F = fft2(f,P,Q);
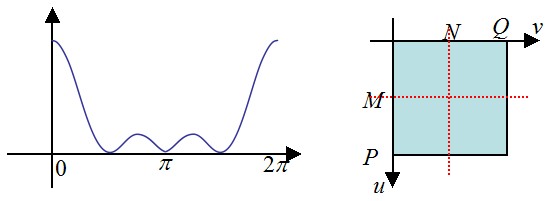
下图画出了本行代码所求取的图像的傅里叶变换的范围(右)和与其等效的一维傅里叶变换的范围(左)。所得到的图像F(u,v)的尺寸为PxQ。
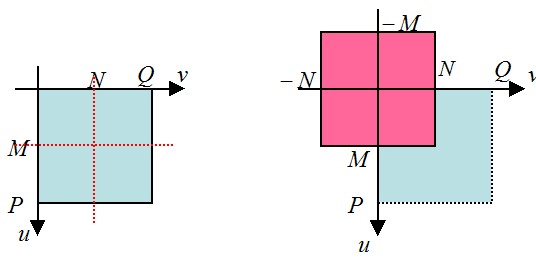
我们需要对其移动一下,如下图所示,我们需要的是粉色范围的区域。
下面,从数学上分析一下,如何获得这个部分的频谱。对于傅里叶变换,有如下性质。
这个特性称为平移特性,粉色部分的频谱,将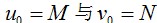
为次,我们已经得到了粉色范围的频谱。越靠近傅里叶频谱图像中间的成分,代表了低频成分。其Matlab代码如下所示。
[plain] view plain copy

 正在上传…重新上传取消
正在上传…重新上传取消![]()
 正在上传…重新上传取消
正在上传…重新上传取消
- [M,N] = size(f);
- P = 2*M;
- Q = 2*N;
- fc = zeros(M,N);
- for x = 1:1:M
- for y = 1:1:N
- fc(x,y) = f(x,y) * (-1)^(x+y);
- end
- end
- F = fft2(fc,P,Q);
代码所得到的结果,如下图所示。
接下来,我们总结一下频域滤波的步骤:
①:先将图像做频域内的水平移动,然后求原图像f(x,y)的DFT,得到其图像的傅里叶谱F(u,v)。
②:与频域滤波器做乘积,
③:求取G(u,v)的IDFT,然后再将图像做频域内的水平移动(移动回去),其结果可能存在寄生的虚数,此时忽略即可。
④:这里使用ifft2函数进行IDFT变换,得到的图像的尺寸为PxQ。切取左上角的MxN的图像,就能得到结果了。
2.低通滤波器
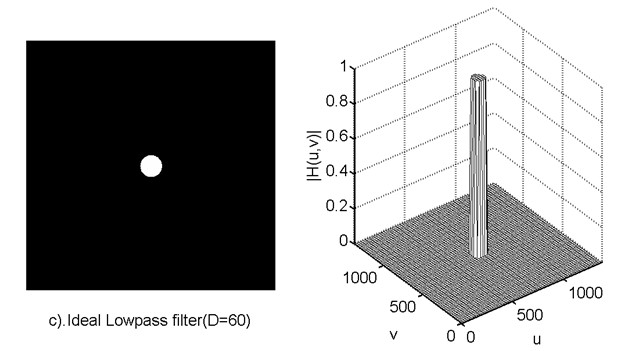
2.1理想的低通滤波器
其中,D0表示通带的半径。D(u,v)的计算方式也就是两点间的距离,很简单就能得到。
使用低通滤波器所得到的结果如下所示。低通滤波器滤除了高频成分,所以使得图像模糊。由于理想低通滤波器的过度特性过于急峻,所以会产生了振铃现象。
2.2巴特沃斯低通滤波器
同样的,D0表示通带的半径,n表示的是巴特沃斯滤波器的次数。随着次数的增加,振铃现象会越来越明显。
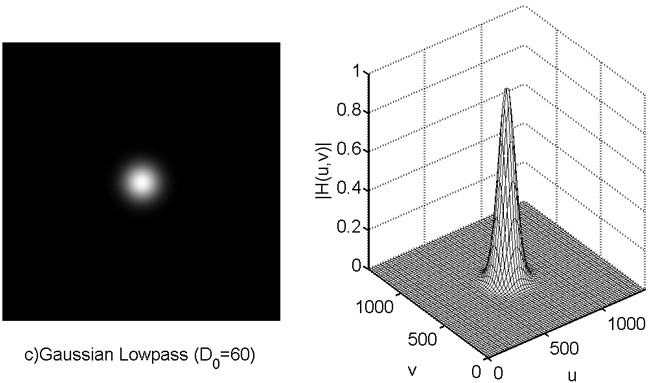
2.3高斯低通滤波器
D0表示通带的半径。高斯滤波器的过度特性非常平坦,因此是不会产生振铃现象的。
3.实现代码
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100 | close all; clear all; %% ---------Butterworth Lowpass Filters (Fre. Domain)------------ f = imread('characters_test_pattern.tif'); f = mat2gray(f,[0 255]); [M,N] = size(f); P = 2*M; Q = 2*N; fc = zeros(M,N); for x = 1:1:M for y = 1:1:N fc(x,y) = f(x,y) * (-1)^(x+y); end end F = fft2(fc,P,Q); H_1 = zeros(P,Q); H_2 = zeros(P,Q); for x = (-P/2):1:(P/2)-1 for y = (-Q/2):1:(Q/2)-1 D = (x^2 + y^2)^(0.5); D_0 = 100; H_1(x+(P/2)+1,y+(Q/2)+1) = 1/(1+(D/D_0)^2); H_2(x+(P/2)+1,y+(Q/2)+1) = 1/(1+(D/D_0)^6); end end G_1 = H_1 .* F; G_2 = H_2 .* F; g_1 = real(ifft2(G_1)); g_1 = g_1(1:1:M,1:1:N); g_2 = real(ifft2(G_2)); g_2 = g_2(1:1:M,1:1:N); for x = 1:1:M for y = 1:1:N g_1(x,y) = g_1(x,y) * (-1)^(x+y); g_2(x,y) = g_2(x,y) * (-1)^(x+y); end end %% -----show------- figure(); subplot(1,2,1); imshow(f,[0 1]); xlabel('a).Original Image'); subplot(1,2,2); imshow(log(1 + abs(F)),[ ]); xlabel('b).Fourier spectrum of a'); figure(); subplot(1,2,1); imshow(H_1,[0 1]); xlabel('c)Butterworth Lowpass (D_{0}=100,n=1)'); subplot(1,2,2); h = mesh(1:20:P,1:20:Q,H_1(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 P 0 Q 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,1); imshow(log(1 + abs(G_1)),[ ]); xlabel('d).Result of filtering using c'); subplot(1,2,2); imshow(g_1,[0 1]); xlabel('e).Result image'); figure(); subplot(1,2,1); imshow(H_2,[0 1]); xlabel('f).Butterworth Lowpass (D_{0}=100,n=3)'); subplot(1,2,2); h = mesh(1:20:P,1:20:Q,H_2(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 P 0 Q 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,1); imshow(log(1 + abs(G_2)),[ ]); xlabel('g).Result of filtering using e'); subplot(1,2,2); imshow(g_2,[0 1]); xlabel('h).Result image'); |
Butterworth_Lowpass_Filters.m
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103 | close all; clear all; clc; %% ---------Gaussian Lowpass Filters (Fre. Domain)------------ f = imread('characters_test_pattern.tif'); f = mat2gray(f,[0 255]); [M,N] = size(f); P = 2*M; Q = 2*N; fc = zeros(M,N); for x = 1:1:M for y = 1:1:N fc(x,y) = f(x,y) * (-1)^(x+y); end end F = fft2(fc,P,Q); H_1 = zeros(P,Q); H_2 = zeros(P,Q); for x = (-P/2):1:(P/2)-1 for y = (-Q/2):1:(Q/2)-1 D = (x^2 + y^2)^(0.5); D_0 = 60; H_1(x+(P/2)+1,y+(Q/2)+1) = exp(-(D*D)/(2*D_0*D_0)); D_0 = 160; H_2(x+(P/2)+1,y+(Q/2)+1) = exp(-(D*D)/(2*D_0*D_0)); end end G_1 = H_1 .* F; G_2 = H_2 .* F; g_1 = real(ifft2(G_1)); g_1 = g_1(1:1:M,1:1:N); g_2 = real(ifft2(G_2)); g_2 = g_2(1:1:M,1:1:N); for x = 1:1:M for y = 1:1:N g_1(x,y) = g_1(x,y) * (-1)^(x+y); g_2(x,y) = g_2(x,y) * (-1)^(x+y); end end %% -----show------- close all; figure(); subplot(1,2,1); imshow(f,[0 1]); xlabel('a).Original Image'); subplot(1,2,2); imshow(log(1 + abs(F)),[ ]); xlabel('b).Fourier spectrum of a'); figure(); subplot(1,2,1); imshow(H_1,[0 1]); xlabel('c)Gaussian Lowpass (D_{0}=60)'); subplot(1,2,2); h = mesh(1:20:P,1:20:Q,H_1(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 P 0 Q 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,1); imshow(log(1 + abs(G_1)),[ ]); xlabel('d).Result of filtering using c'); subplot(1,2,2); imshow(g_1,[0 1]); xlabel('e).Result image'); figure(); subplot(1,2,1); imshow(H_2,[0 1]); xlabel('f).Gaussian Lowpass (D_{0}=160)'); subplot(1,2,2); h = mesh(1:20:P,1:20:Q,H_2(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 P 0 Q 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,1); imshow(log(1 + abs(G_2)),[ ]); xlabel('g).Result of filtering using e'); subplot(1,2,2); imshow(g_2,[0 1]); xlabel('h).Result image'); |
Gaussian_Lowpass_Filters.m
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798 | close all; clear all; %% ---------Ideal Lowpass Filters (Fre. Domain)------------ f = imread('characters_test_pattern.tif'); f = mat2gray(f,[0 255]); [M,N] = size(f); P = 2*M; Q = 2*N; fc = zeros(M,N); for x = 1:1:M for y = 1:1:N fc(x,y) = f(x,y) * (-1)^(x+y); end end F = fft2(fc,P,Q); H_1 = zeros(P,Q); H_2 = zeros(P,Q); for x = (-P/2):1:(P/2)-1 for y = (-Q/2):1:(Q/2)-1 D = (x^2 + y^2)^(0.5); if(D <= 60) H_1(x+(P/2)+1,y+(Q/2)+1) = 1; end if(D <= 160) H_2(x+(P/2)+1,y+(Q/2)+1) = 1; end end end G_1 = H_1 .* F; G_2 = H_2 .* F; g_1 = real(ifft2(G_1)); g_1 = g_1(1:1:M,1:1:N); g_2 = real(ifft2(G_2)); g_2 = g_2(1:1:M,1:1:N); for x = 1:1:M for y = 1:1:N g_1(x,y) = g_1(x,y) * (-1)^(x+y); g_2(x,y) = g_2(x,y) * (-1)^(x+y); end end %% -----show------- figure(); subplot(1,2,1); imshow(f,[0 1]); xlabel('a).Original Image'); subplot(1,2,2); imshow(log(1 + abs(F)),[ ]); xlabel('b).Fourier spectrum of a'); figure(); subplot(1,2,1); imshow(H_1,[0 1]); xlabel('c).Ideal Lowpass filter(D=60)'); subplot(1,2,2); h = mesh(1:20:P,1:20:Q,H_1(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 P 0 Q 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,1); imshow(log(1 + abs(G_1)),[ ]); xlabel('d).Result of filtering using c'); subplot(1,2,2); imshow(g_1,[0 1]); xlabel('e).Result image'); figure(); subplot(1,2,1); imshow(H_2,[0 1]); xlabel('f).Ideal Lowpass filter(D=160)'); subplot(1,2,2); h = mesh(1:20:P,1:20:Q,H_2(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 P 0 Q 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,1); imshow(log(1 + abs(G_2)),[ ]); xlabel('g).Result of filtering using e'); subplot(1,2,2); imshow(g_2,[0 1]); xlabel('h).Result image'); |