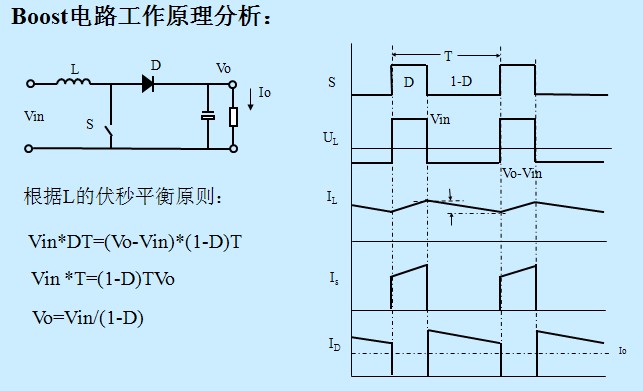
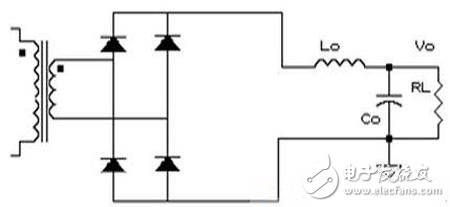
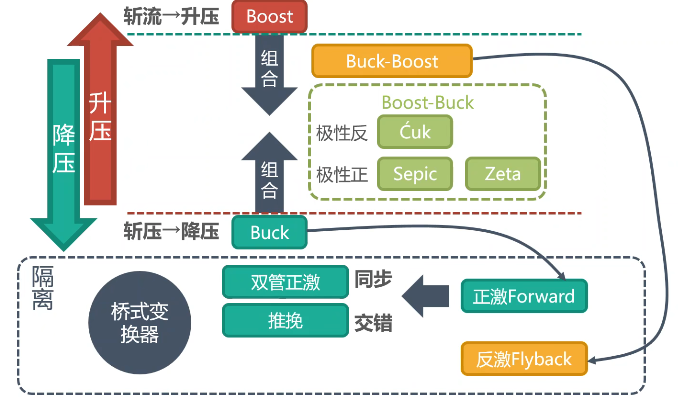
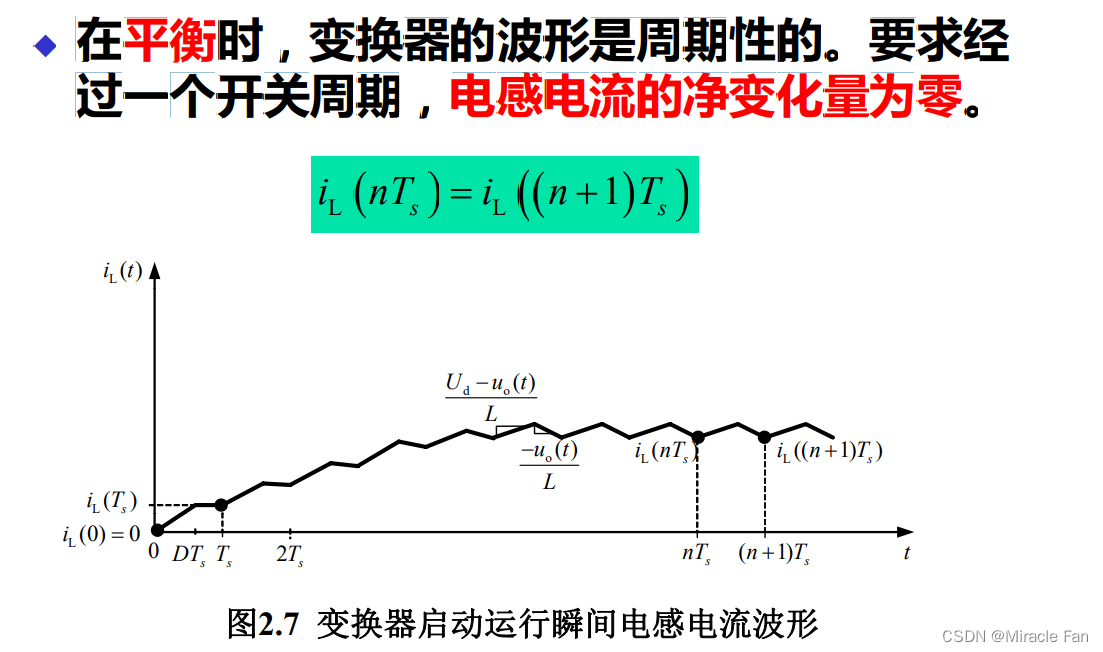
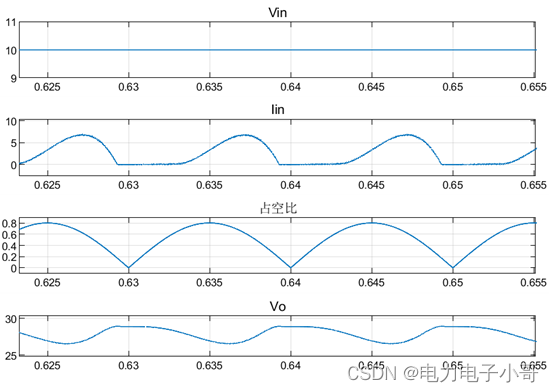
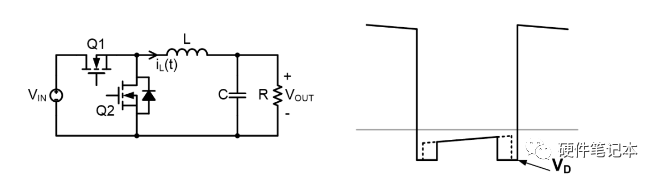
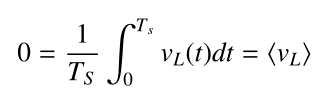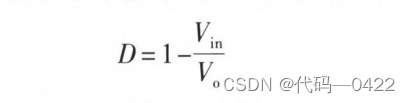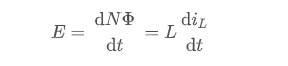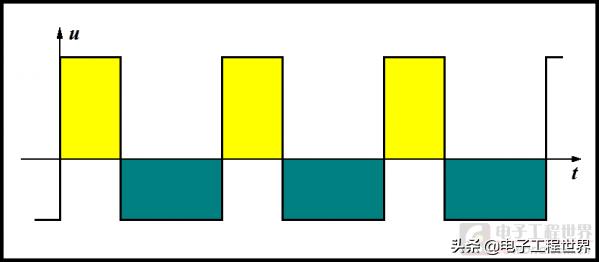2.4 Cuk电路分析
-
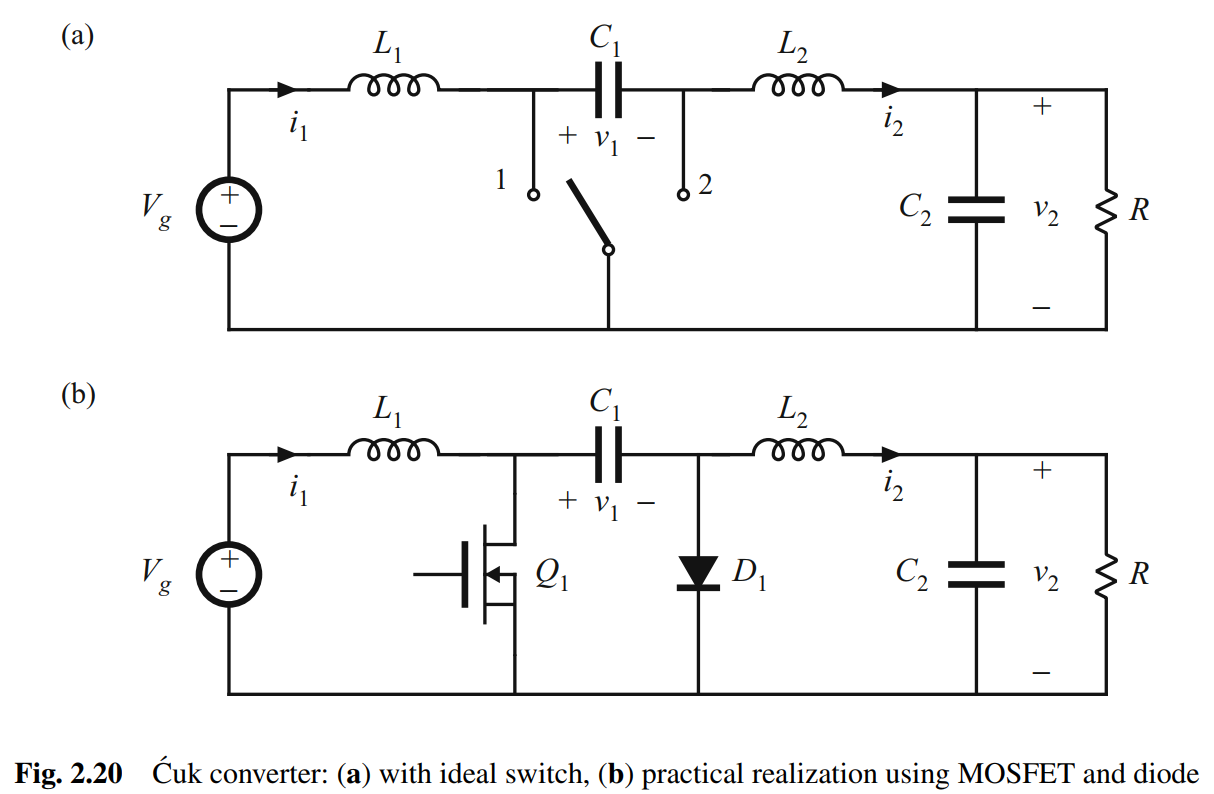
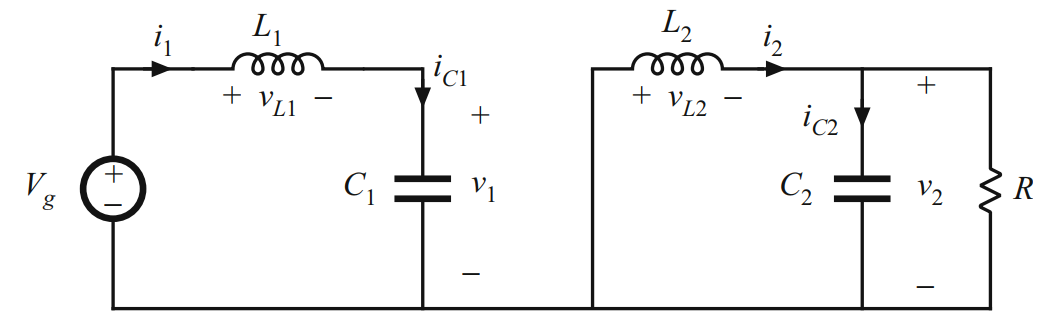
作为第二个示例,变换器可以实现类似buck-boost电路功能:升高或降低电压幅值,并且转换极性。其电路如如下。
-
该转换器通过电容进行能量传输。当开关打到位置2时,电容 C 1 C_1 C1通过 L 1 L_1 L1连到输入电源,电源能量存储在 C 1 C_1 C1中。当开关打到位置1时, C 1 C_1 C1存储的能量通过电感 L 2 L_2 L2释放到输出端。
-
如图,定义了电感电压和电容电流,并任意分配了参考方向(极性),利用前面提到的电感伏秒平衡、电容电荷平衡及低纹波近似计算电路等式。
-
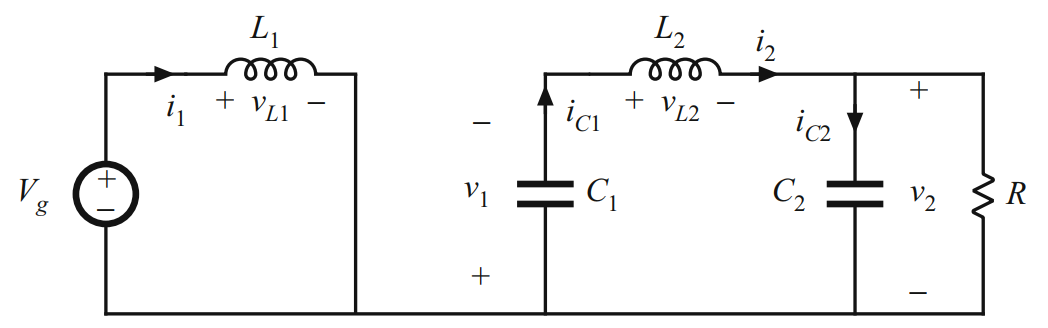
在第一个子区间内,开关打到位置1,电路简化为
-
电感电压和电容电流等式如下,且使用低纹波近似 v L 1 = V g v_{L1}=V_g vL1=Vg v L 2 = − v 1 − v 2 ≈ − V 1 − V 2 v_{L2}=-v_1-v_2 \approx -V_1-V_2 vL2=−v1−v2≈−V1−V2 i C 1 = i 2 ≈ I 2 i_{C1}=i_2 \approx I_2 iC1=i2≈I2 i C 2 = i 2 − v 2 R ≈ I 2 − V 2 R i_{C2}=i_2-\frac{v_2}{R} \approx I_2-\frac{V_2}{R} iC2=i2−Rv2≈I2−RV2
-
在第二个子区间内,开关打到2位置,电路简化为
-
电感电压和电容电流等式如下,且使用低纹波近似 v L 1 = V g − v 1 ≈ V g − V 1 v_{L1}=V_g-v_1 \approx V_g-V_1 vL1=Vg−v1≈Vg−V1 v L 2 = − v 2 ≈ − V 2 v_{L2}=-v_2 \approx -V_2 vL2=−v2≈−V2 i C 1 = i 1 ≈ I 1 i_{C1}=i_1 \approx I_1 iC1=i1≈I1 i C 2 = i 2 − v 2 R ≈ I 2 − V 2 R i_{C2}=i_2- \frac{v_2}{R} \approx I_2-\frac{V_2}{R} iC2=i2−Rv2≈I2−RV2
-
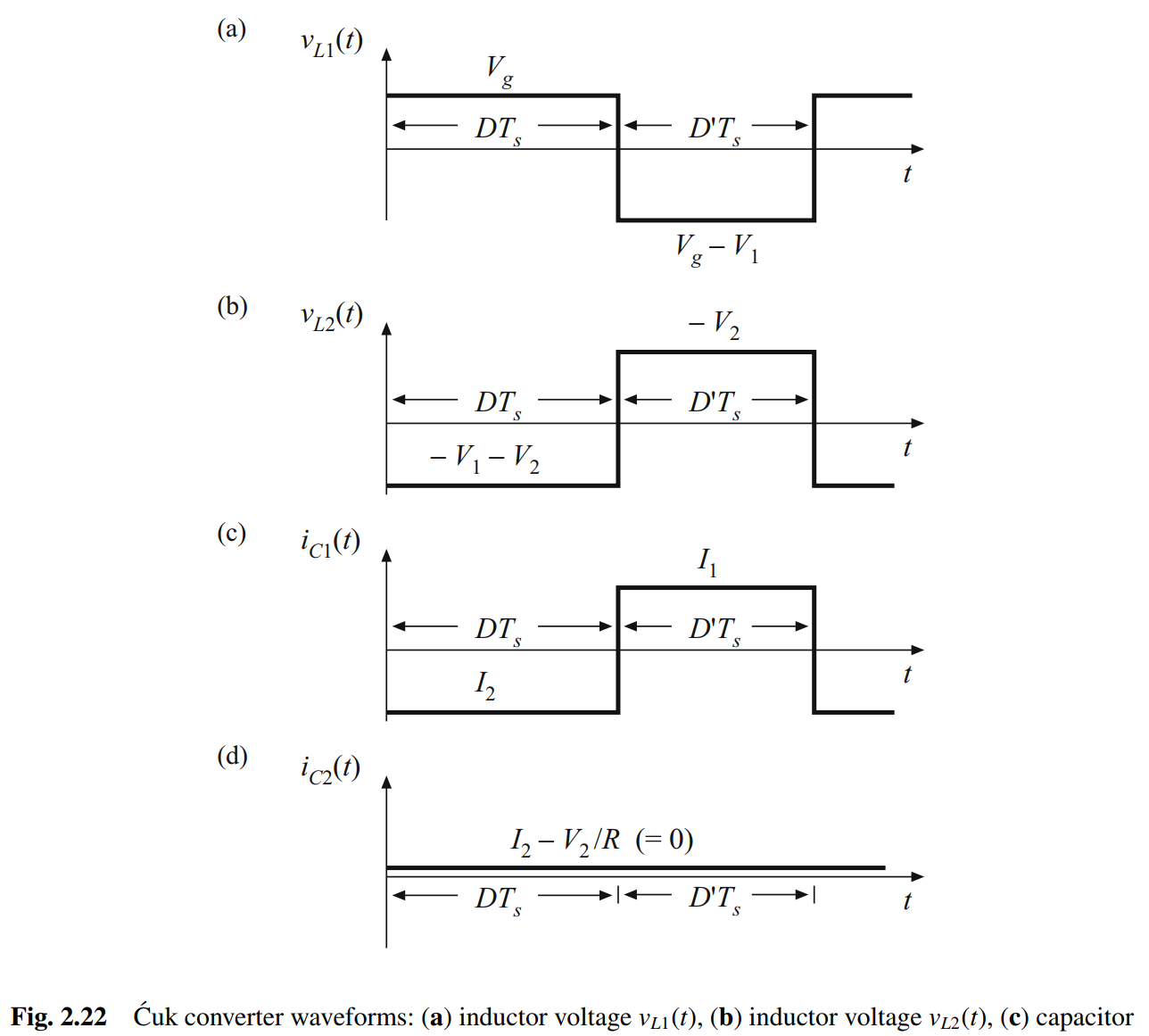
整个电路波形如下
-
将波形的直流分量或平均值等效为零,以找到变换器中的稳态条件。有 < v L 1 > = V g ∗ D + ( V g − V 1 ) ∗ D ′ = 0 <v_{L1}>=V_g*D+(V_g-V_1)*D'=0 <vL1>=Vg∗D+(Vg−V1)∗D′=0 < v L 2 > = ( − V 1 − V 2 ) ∗ D + ( − V 2 ) ∗ D ′ = 0 <v_{L2}>=(-V_1-V_2)*D+(-V_2)*D'=0 <vL2>=(−V1−V2)∗D+(−V2)∗D′=0 < i C 1 > = I 2 ∗ D + I 1 ∗ D ′ = 0 <i_{C1}>=I_2*D+I_1*D'=0 <iC1>=I2∗D+I1∗D′=0 < i C 2 > = I 2 − V 2 R = 0 <i_{C2}>=I_2-\frac{V_2}{R}=0 <iC2>=I2−RV2=0
-
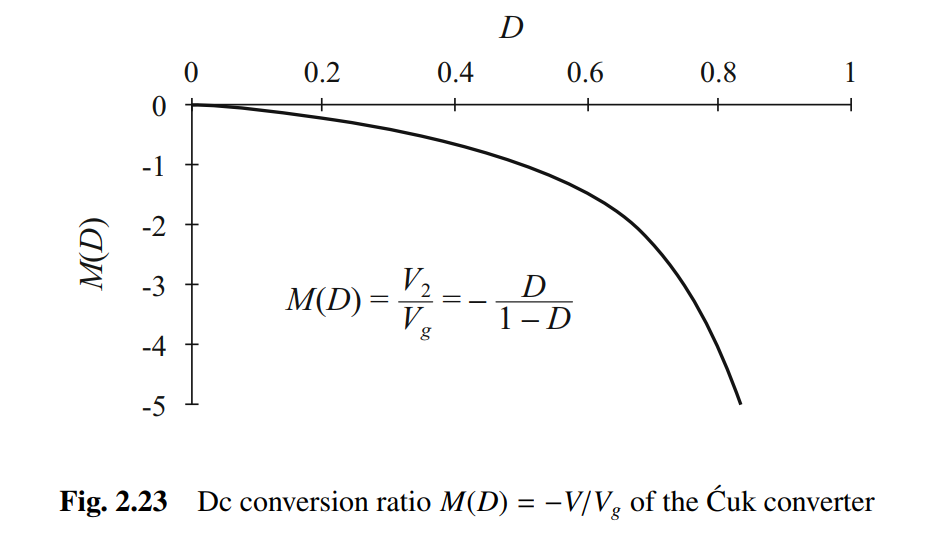
可求得电容电压和电感电流为 V 1 = V g D ′ V_1=\frac{V_g}{D'} V1=D′Vg V 2 = − V 1 D = − D D ′ V g V_2=-V_1D=-\frac{D}{D'}V_g V2=−V1D=−D′DVg I 1 = − D D ′ I 2 = ( D D ′ ) 2 V g R I_1=-\frac{D}{D'}I_2=(\frac{D}{D'})^2\frac{V_g}{R} I1=−D′DI2=(D′D)2RVg I 2 = − D D ′ V g R I_2=-\frac{D}{D'}\frac{V_g}{R} I2=−D′DRVg
-
直流输出 V 2 V_2 V2与占空比 D D D之间关系
-
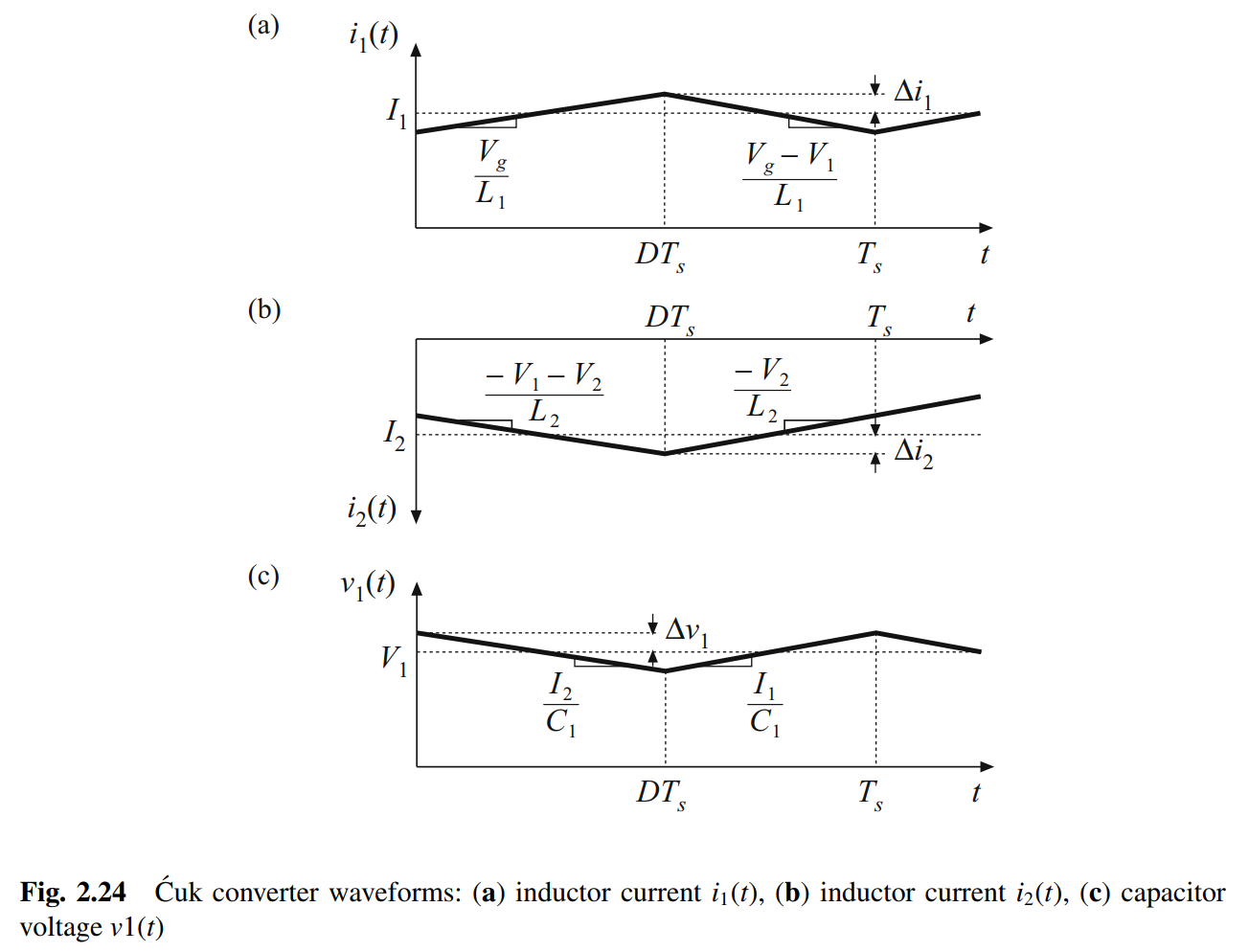
电感电流波形、电容电压波形如下
-
在第一个子区间内,各波形斜率为 d i 1 ( t ) d t = v L 1 ( t ) L 1 = V g L 1 \frac{di_1(t)}{dt}=\frac{v_{L1}(t)}{L_1}=\frac{V_g}{L_1} dtdi1(t)=L1vL1(t)=L1Vg d i 2 ( t ) d t = v L 2 ( t ) L 2 = − V 1 − V 2 L 2 \frac{di_2(t)}{dt}=\frac{v_{L2}(t)}{L_2}=\frac{-V_1-V_2}{L_2} dtdi2(t)=L2vL2(t)=L2−V1−V2 d v 1 ( t ) d t = i C 1 ( t ) C 1 = I 2 C 1 \frac{dv_1(t)}{dt}=\frac{i_{C1}(t)}{C_1}=\frac{I_2}{C_1} dtdv1(t)=C1iC1(t)=C1I2
-
在第二个子区间内,各波形斜率为 d i 1 ( t ) d t = v L 1 ( t ) L 1 = V g − V 1 L 1 \frac{di_1(t)}{dt}=\frac{v_{L1}(t)}{L_1}=\frac{V_g-V_1}{L_1} dtdi1(t)=L1vL1(t)=L1Vg−V1 d i 2 ( t ) d t = v L 2 ( t ) L 2 = − V 2 L 2 \frac{di_2(t)}{dt}=\frac{v_{L2}(t)}{L_2}=\frac{-V_2}{L_2} dtdi2(t)=L2vL2(t)=L2−V2 d v 1 ( t ) d t = i C 1 ( t ) C 1 = I 1 C 1 \frac{dv_1(t)}{dt}=\frac{i_{C1}(t)}{C_1}=\frac{I_1}{C_1} dtdv1(t)=C1iC1(t)=C1I1
-
利用这些等式求取电容容值或电压纹波、电感感量或电流纹波。在第一个子区间内,从 0 0 0到 D T s DT_s DTs, i 1 ( t ) 、 i 2 ( t ) 、 v 1 ( t ) i_1(t)、i_2(t)、v_1(t) i1(t)、i2(t)、v1(t)的变化分别为 2 Δ i 1 、 − 2 Δ i 2 、 − 2 Δ v 1 2Δi_1、-2Δi_2、-2Δv_1 2Δi1、−2Δi2、−2Δv1,则根据上面等式可得 2 Δ i 1 = V g L 1 ∗ D T s → Δ i 1 = V g 2 L 1 ∗ D T s 2Δi_1=\frac{V_g}{L_1} *DT_s → Δi_1=\frac{V_g}{2L_1} *DT_s 2Δi1=L1Vg∗DTs→Δi1=2L1Vg∗DTs − 2 Δ i 2 = − V 1 − V 2 L 2 ∗ D T s → Δ i 2 = V 1 + V 2 2 L 2 ∗ D T s -2Δi_2=\frac{-V_1-V_2}{L_2}*DT_s → Δi_2=\frac{V_1+V_2}{2L_2}*DT_s −2Δi2=L2−V1−V2∗DTs→Δi2=2L2V1+V2∗DTs − 2 Δ v 1 = I 2 C 1 ∗ D T s → Δ v 1 = − I 2 2 C 1 ∗ D T s -2Δv_1=\frac{I_2}{C_1}*DT_s → Δv_1=-\frac{I_2}{2C_1}*DT_s −2Δv1=C1I2∗DTs→Δv1=−2C1I2∗DTs
-
在根据上面已经求得的 V 1 、 V 2 、 V g 、 D V_1、V_2、V_g、D V1、V2、Vg、D的关系表达式,可得 Δ i 1 = V g D T s 2 L 1 Δi_1=\frac{V_gDT_s}{2L_1} Δi1=2L1VgDTs Δ i 2 = V g D T s 2 L 2 Δi_2=\frac{V_gDT_s}{2L_2} Δi2=2L2VgDTs Δ v 1 = V g D 2 T s 2 D ′ R C 1 Δv_1=\frac{V_gD^2T_s}{2D'RC_1} Δv1=2D′RC1VgD2Ts
-
同样的,这些公式可以在各个纹波变量确定后,确定 L 1 、 L 2 、 C 1 L_1、L_2、C_1 L1、L2、C1。
-
类似的方法不能用来计算输出滤波电容 C 2 C_2 C2的 V 2 ( t ) V_2(t) V2(t)的纹波幅值。根据上面的波形图可以发现,电容电流 i C 2 ( t ) i_{C2}(t) iC2(t)是连续的。如果 i 2 ( t ) i_2(t) i2(t)的开关纹波被忽略了,那么 i C 2 ( t ) i_{C2}(t) iC2(t)就不含交流分量,根据小纹波近似,输出开关纹波 Δ v 2 = 0 Δv_2=0 Δv2=0。可以确定的是,输出电压纹波并不是0,要估算变换器输出电压纹波大小,就不能忽略电感电流 i L 2 ( t ) i_{L2}(t) iL2(t)中的开关纹波,因为这个开关纹波是输出电容电压波动的唯一交流来源。