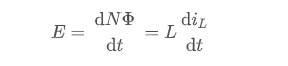直流-直流交换技术

DC-DC变换电路的工作原理

DC-DC变换电路（直流斩波电路）：

• 作用：将直流电变成另一固定电压或可调电压的直流电

输出直流的平均电压：
$$U_0=\frac{1}{T}{\int }_0^{t_{on}}{U}_{S}dt=\frac{t_{\text{on }}}{T}{U}_S=D{U}_S$$

• $D=\frac{t_{on}}{T}$被称为导通占空比
• 通过改变占空比D，即可改变负载R上的直流平均电压

脉冲调制方式

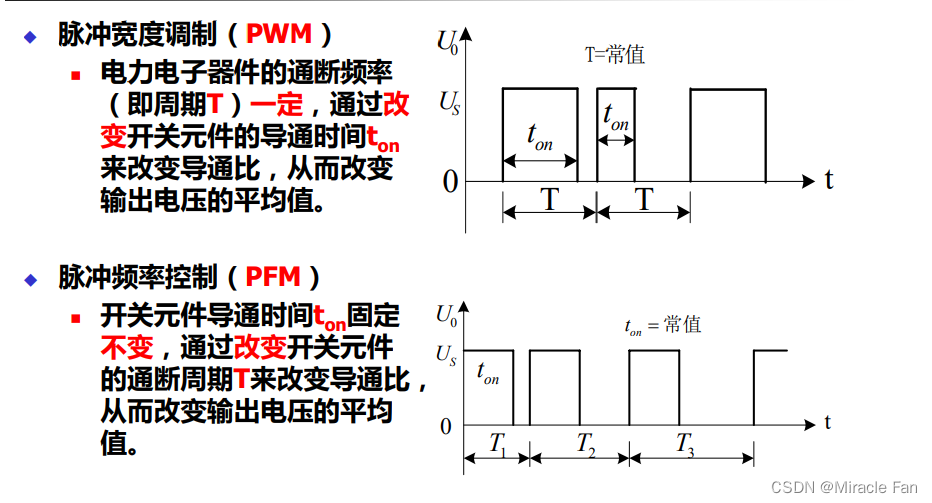
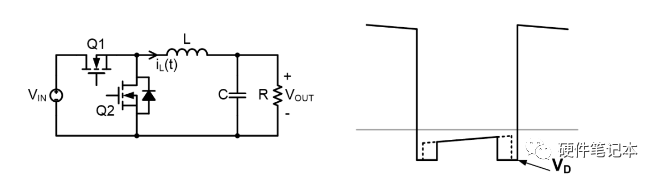
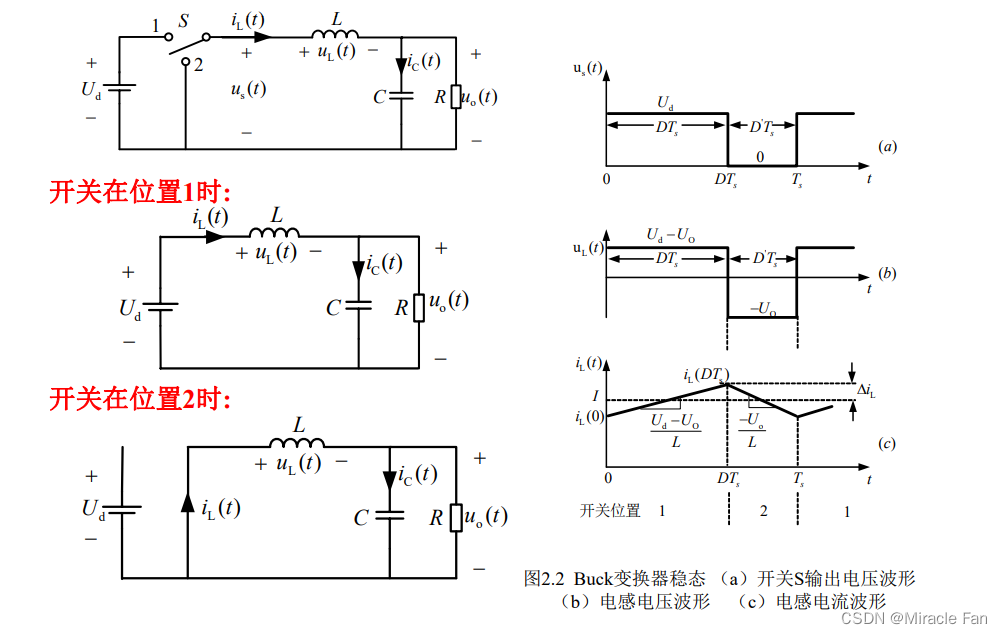
Buck电路

基本输入输出关系

• 电感L和电容C组成低通滤波器，设计原则是:使$u_s(t)$的直流分量可以通过电感L，而抑制$u_s(t)$的开关频率以及谐波分量进入。

• $u_s(t)$的直流成分是其平均值$⟨u_s⟩$
  $$⟨u_s⟩=\frac{1}{T_S}{\int }_0^{T_s}{u}_s(t)dt=\frac{1}{T_s}\left(D{T}_s{U}_{\mathrm{d}}\right)=D{U}_{\mathrm{d}}$$

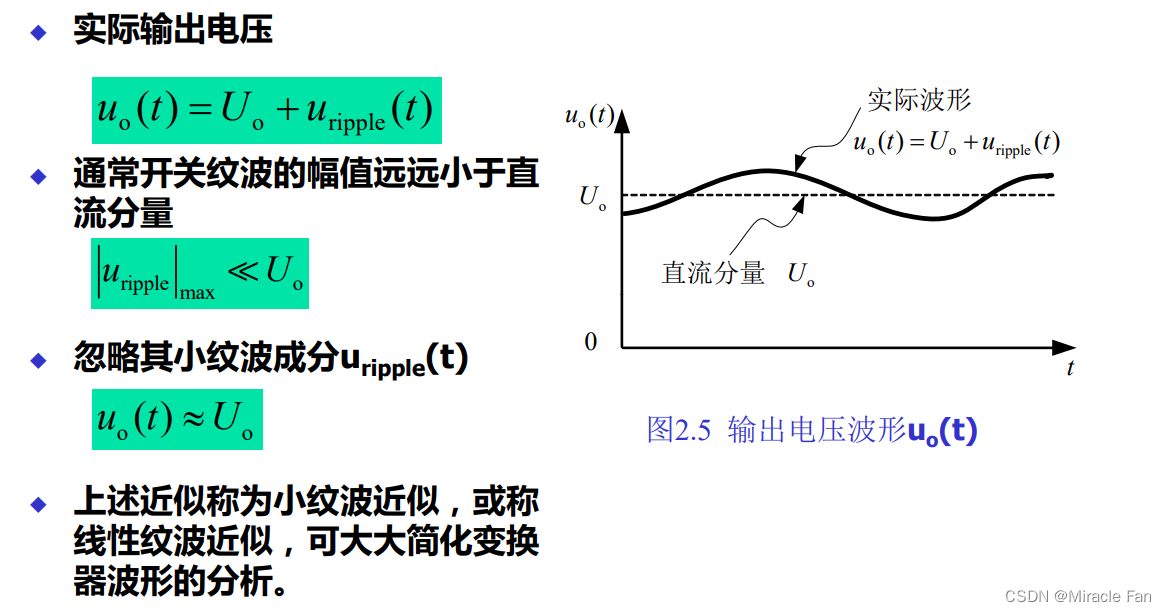
• 稳态时，输出电压$u_0(t)$的平均值为$U_0$
  $$U_0=⟨u_s⟩=D{U}_d$$

• 电压变换比为：
  $$\frac{U_0}{U_d}=D$$

电感伏秒平衡和电容充电平衡

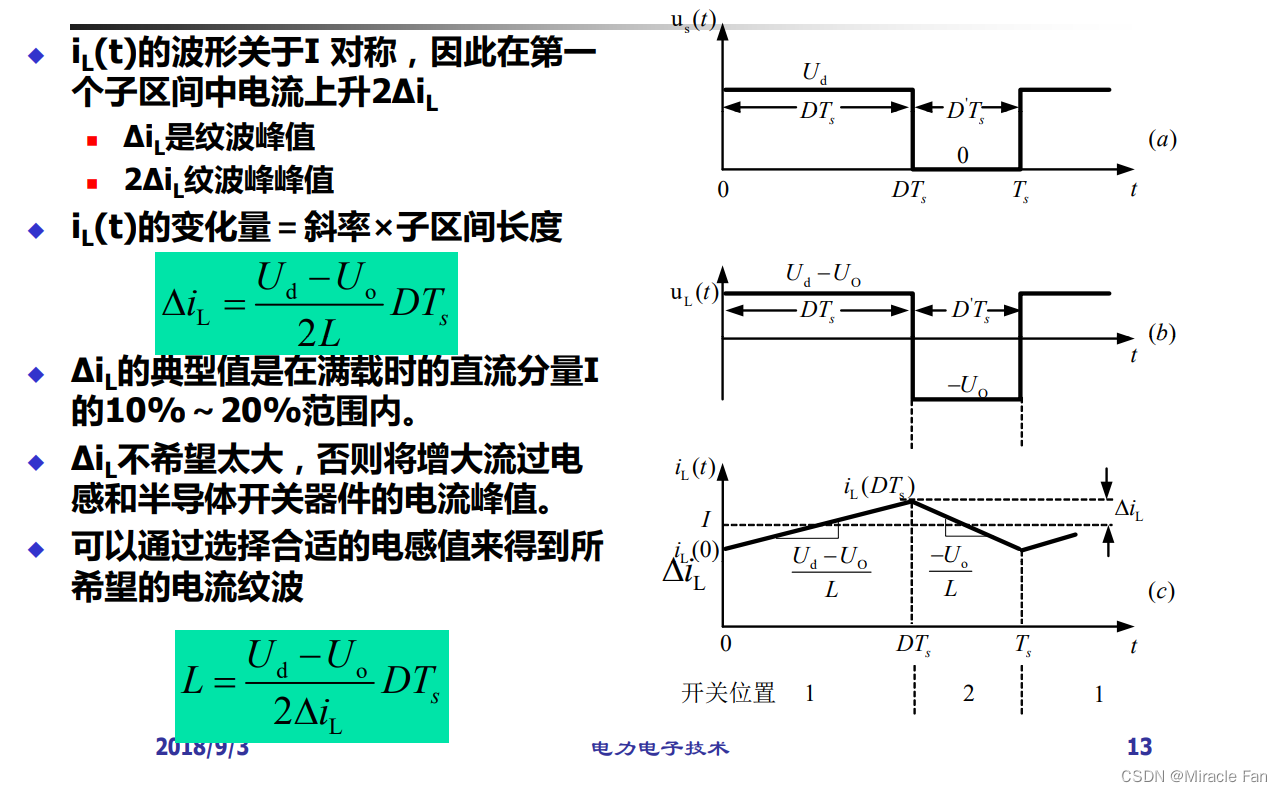
电感的伏秒平衡

用于推导输出电压的直流成分

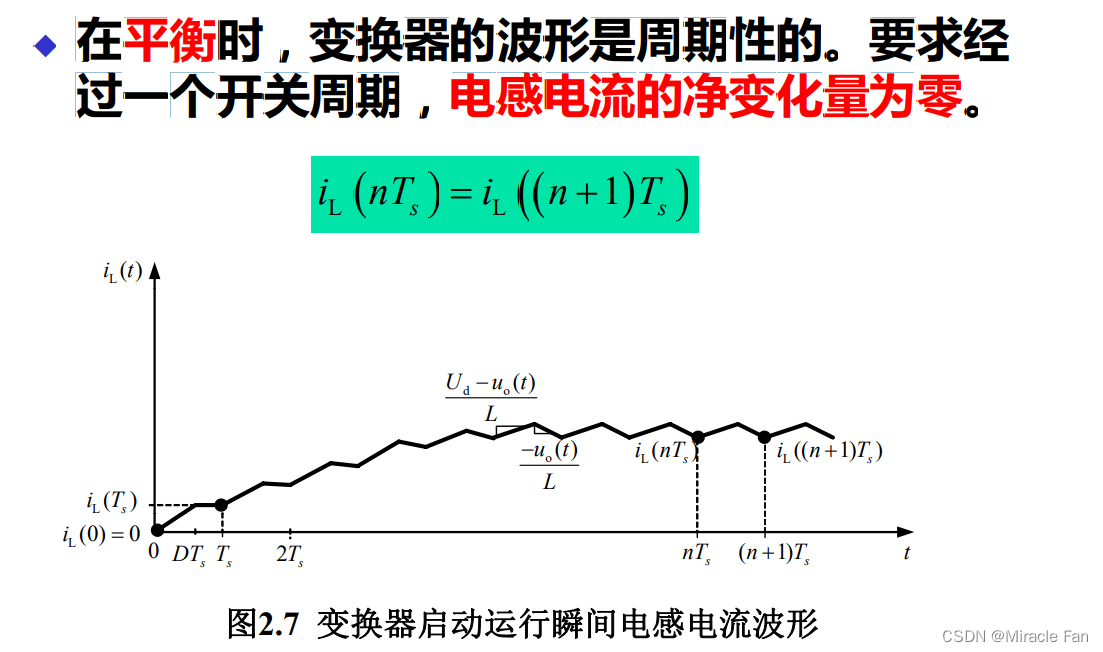
基于这一点，可以寻找到任意开关变换器中的一个稳态条件：电感伏秒平衡原理。对于电感：
$$u_{\mathrm{L}}(t)=L\frac{\mathrm{d}{i}_{\mathrm{L}}(t)}{\mathrm{d}t}$$
从0~$T_s$进行一个周期的积分，得到：
$$i_{\mathrm{L}}\left(T_s\right)-i_{\mathrm{L}}(0)=\frac{1}{L}{\int }_0^{T_s}{u}_{\mathrm{L}}(t)\mathrm{d}t$$
而显然在一个周期中左侧为0，因此在稳态状态下，电感电压的周期积分为0
$$⟨u_L⟩=\frac{1}{T_s}{\int }_0^{T_s}{u}_{\mathrm{L}}(t)\mathrm{d}t=0$$

电容安秒平衡

用于推到开关变换器的稳态电流
$$\begin{gathered} i_{\mathrm{C}}(t)=C\frac{\mathrm{d}{u}_{\mathrm{C}}(t)}{\mathrm{d}t} \\ {u}_{\mathrm{C}}\left(T_s\right)-u_{\mathrm{C}}(0)=\frac{1}{C}{\int }_0^{T_s}{i}_{\mathrm{C}}(t)dt=0 \end{gathered}$$
因此，在平衡时，一个开关周期中电容电流的积分为0，稳态时电容充电没有净变化量，其等价表达式为：
$$0=\frac{1}{T_s}{\int }_0^{T_s}{i}_{\mathrm{C}}(t)dt=⟨i_{\mathrm{C}}⟩$$
我们可以从一个直观结果去认识电感伏秒平衡和电容充电平衡。比如若一个周期有直流电流流入电容，那么电容将连续充电，而其电压也会无线上升，同理对于电感，其磁通连续上升，电流也会无线上升，这显然是不合理的。