转载+原创

函数优化

函数最值

函数最值

该例子参考 深入浅出遗传算法，透析GA本质.（强烈安利）中的例子，加上了一些自己的理解和改动
ex：已知x为整数，求在区间[0,31]区间上的二次函数y=x^2的最大值（max:x2）
分析：
个体：区间上的每一个x；适应度 f(x)=x^2；解空间 [0，31]

解：

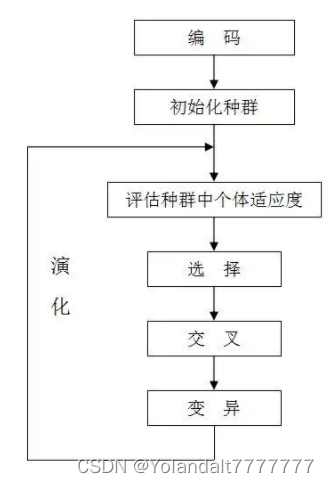
1. 设定种群规模；编码；产生初始种群
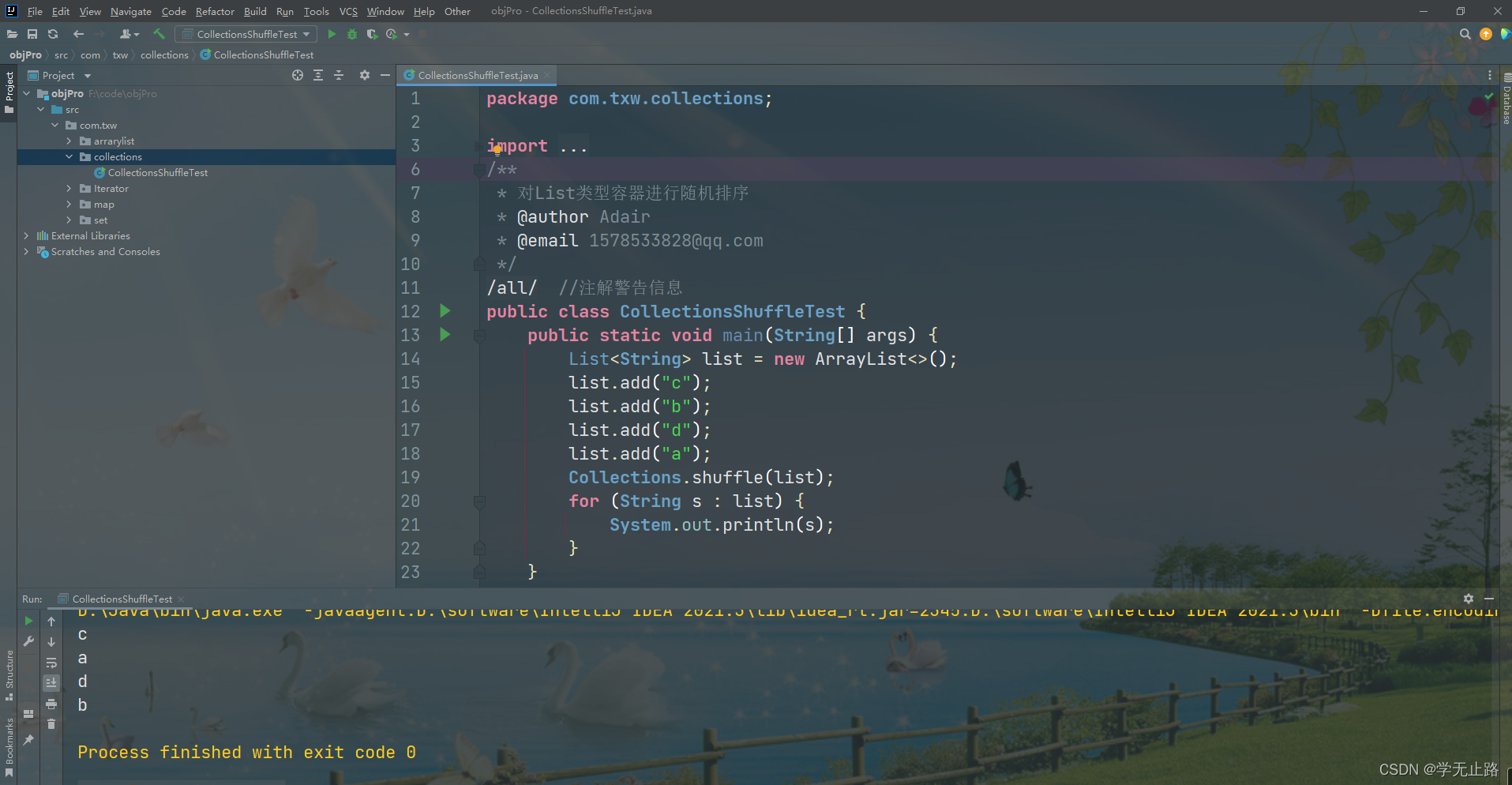
   设种群规模为4；用二进制数编码；取已下个体为初始种群：
   13（01101）
   24（11000）
   8 （01000）
   19（10011）

2. 设定适应度函数
   令f(x) = x^2

3. 计算各代种群中的个体适应度，对染色体进行遗传操作，直到个体适应度最高的个体出现
   由f(x) = x^2计算适应值、由f(xi)/ΣF(xi)计算选择概率、再逐个累加得积累概率 填入下表。
   设 从[0,1]区间产生4个随机数：
   r1 = 0.329876
   r2 = 0.098798
   r3 = 0.580045
   r4 = 0.790431
   代入积累概率区间可得选中次数分别为

编号	初始群体	变量x	适应值f(x)	选择比	积累概率	选中次数
1	0 1 1 0 1	13	169	0.14	0.14	1
2	1 1 0 0 0	24	576	0.49	0.63	2
3	0 1 0 0 0	8	64	0.06	0.69	0
4	1 0 0 1 1	19	361	0.31	1.00	1
和	-------------	------------	1170	1	------------	4
平均值	-------------	------------	293	0.25	------------	1
最大值	-------------	24	576	0.49	------------	2

于是经复制得到到：
13（01101）
24（11000）
24（11000）
19（10011）
假设交叉率Pc=100%，作交叉操作(1和2、3和4)

编号	交配池	交叉位置	交叉后的新种群	变量x	适应值f(x)
1	0 1 1 0 \ 1	4	0 1 1 0 0	12	144
2	1 1 0 0 \ 0	4	1 1 0 0 1	25	625
3	1 1 \ 0 0 0	2	1 1 0 1 1	27	729
4	1 0 \ 0 1 1	2	1 0 0 0 0	16	256
和					1754
最大值				27	729
平均值					439

假设变异率Pm=0.001，则S1中基因数为：
4(个体数)×5(五位二进制)×0.001 = 0.02
不足1，因此不会产生变异

---

如若存在变异，则做如下操作：
假设变异基因数为1

编号	交叉后的新种群	变异后的新种群	变量x	适应值f(x)
1	0 1 1 0 0	1 1 1 0 0	28	784
2	1 1 0 0 1	1 1 0 0 1	25	625
3	1 1 0 1 1	1 1 0 1 1	27	729
4	1 0 0 0 0	1 0 0 0 0	16	256

重复上述选择交叉操作直到出现x≥31

---

现在，回到交叉操作之后，不产生变异，所以该轮遗传染色体不发生改变，得到S2种群。重复选择交叉操作
交叉：

编号	S2种群	变量x	适应值f(x)	选择比	累积概率	估计选中次数
1	0 1 1 0 0	12	144	0.08	0.08	0
2	1 1 0 0 1	25	625	0.36	0.44	1
3	1 1 0 1 1	27	729	0.41	0.85	2
4	1 0 0 0 0	16	256	0.15	1.00	1

若都选中（ps：若不产生变异，如需得到最大值31，则必须保留第三位的基因1）
得到交配池：
12（0 1 1 0 0）
25（1 1 0 0 1）
27（1 1 0 1 1）
16（1 0 0 0 0）

编号	交配池	交叉位置	交叉后的新种群	变量x	适应值f(x)
1	0 1 \ 1 0 0	3	0 1 0 0 1	9	81
2	1 1 \ 0 0 1	3	1 1 1 0 0	28	784
3	1 1 \ 0 1 1	3	1 1 0 0 0	24	576
4	1 0 \ 0 0 0	3	1 0 0 1 1	19	361

同样不产生变异，得到S3
继续选择交叉

编号	S3	变量x	适应值f(x)	选择比	累积概率	估计选中次数
1	0 1 0 0 1	9	81	0.04	0.04	0
2	1 1 1 0 0	28	784	0.44	0.48	2
3	1 1 0 0 0	24	576	0.32	0.80	1
4	1 0 0 1 1	19	361	0.20	1.00	1

于是按照估计选择次数选择，得到交配池
28（1 1 1 0 0）
28（1 1 1 0 0）
24（1 1 0 0 0）
19（1 0 0 1 1）
交叉1和4后两位即得到31（1 1 1 1 1）

即适应度最高的染色体出现，遗传结束
代入验证，31为目标函数的最优解。

多个局部最优解问题

例如：

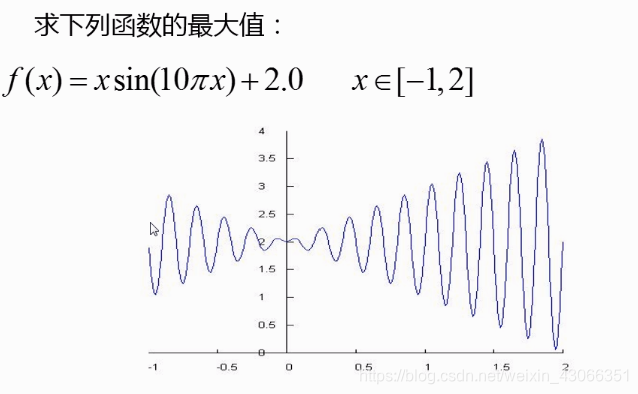
这类问题主要在于解码和解码函数的构造

就可以将实数转化为二进制码，然后进行遗传操作，直到出现最大适应值染色体
具体细节不展开叙述

组合优化

组合（最）优化问题是最优化问题的一类。最优化问题似乎自然地分成两类：一类是连续变量的问题，另一类是离散变量的问题。具有离散变量的问题，我们称它为组合的。在连续变量的问题里，一般地是求一组实数，或者一个函数；在组合问题里，是从一个无限集或者可数无限集里寻找一个对象——典型地是一个整数，一个集合，一个排列，或者一个图。一般地，这两类问题有相当不同的特色，并且求解它们的方法也是很不同的。
来源：《组合最优化算法和复杂性》，高等教育出版社，1988，C.H. Papadimitriou, K. Steiglitz （刘振宏，蔡茂诚 译）

其中 旅行商问题和背包问题都属于组合优化问题

旅行商问题

巡回旅行商问题戳这里

下面讨论背包问题

背包问题

背包问题可以简单描述如下：
一群海盗发现了一处宝藏，里面有各种价值和重量的珍宝，但是珍宝数量巨大，海盗们只有一艘海盗船来装珍宝，那么海盗们要如何组合才能使得拿走的珍宝总价值最大而不超过海盗船的载重量。
数学描述如下：其中
$$p_j为第j件宝物的价值，w_j为第j件珍宝的重量$$

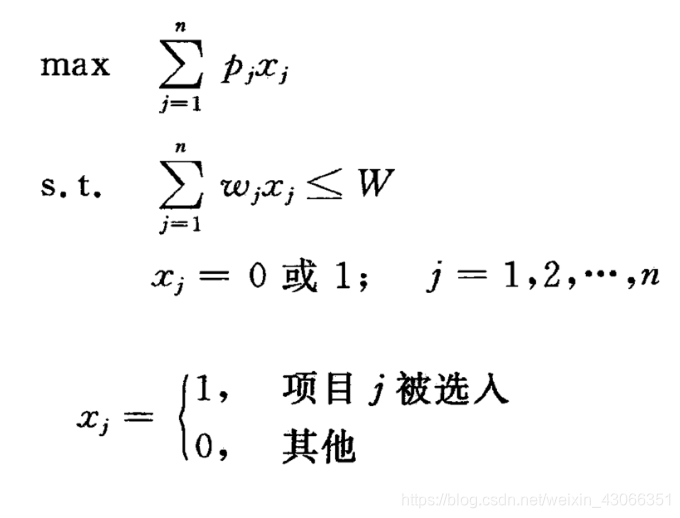
下面讨论**遗传算法（GA）**求解背包问题

二进制表达法

1表示入选、0表示未入选

x	x1	x2	x3	x4	x5
染色体	1	0	0	1	1

以上结果表明x1、x4、x5入选背包

但是该方法可能会产生不可行解（不符合约束条件）或者是入选数量超过承重量。（比较简单粗暴）
解决方法：

1. 惩罚法
   构造惩罚函数p(x)，给每个不可行函数一个简单的罚值
   则适值函数为$$eval(x)=f(x)p(x)$$
   极大化问题的惩罚函数为：
   
   惩罚曲线：
   
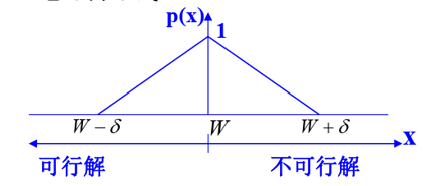
   由此可见，惩罚函数不仅惩罚超过背包承重量的不可行解，也惩罚背包承重量利用不足的可行解。
   最优解位于可行域与不可行域边界上

2. 解码法
   步骤:
   1） 将xj = 1的物品按价值与重量比（单位重量的价值）降序排列
   2）按优先适合启发式选择物品，直到背包不能再装
   ex：

x	x1	x2	x3	x4	x5
染色体	1	0	0	1	1
价值重量比	0.1	——	——	0.5	0.4
降序排列	x4	x5	x1

其中，高亮即为染色体的解

ps：编码和解之间不存在一一对应的关系

顺序表达式

对于一个n 个物品的问题，染色体由n个基因构成，每个基因用一个不同的正整数代表一个物品。

即随机产生一个物品的排列顺序，作为一个染色体，物品再顺序中的位置，可以看作是该物品入选背包的优先级，按物品的顺序用优先适合启发式方法，就可以产生一个可行解（简单来说，就是按物品顺序入选背包、直到背包不能再装）

变长表达法

1）初始化：
首先产生一个随机物品序列，基于这个序列按优先适合启发式构造一个可行背包（染色体长度不定）
2）插入交叉

其中步骤一为 在第一个双亲上选择一个断点，在第二个双亲上选择一截片段，然后将片段插入第一个双亲的断点处。

3）变异

• 随机地删除一个基因
• 以随机的顺序增加染色体中没有的基因（所有没有的基因）
• 对于以上形成的原始后代用优先适合启发式产生一个可行的背包

适值函数的设计

适值函数的设计对算法的性能影响很大
适值函数的设计：

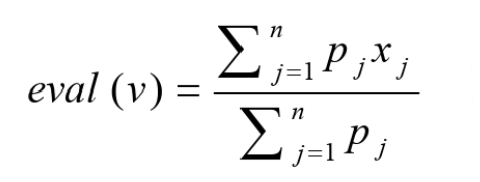
该部分参考https://wenku.baidu.com/view/9b6ecea4cd1755270722192e453610661fd95a63.html

欢迎指正、侵删