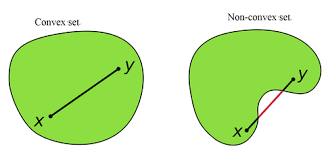
何为优化？

措施：   对应方法

变得更优：      对应的结果更加的好

优化： 动词，一种行为方法----------->目的是获得更好的结果，总之有所改善

优化问题的三要素：

（1) 决策变量

所变：可以改变的量，可以优化的量，通过变量的改变，获得更好的结果。 它可以i理解为控制变量，或者是一些决定性的参数。比如：人的属性特征。      关键：可以改变，  她的改变有助于获得更好的解

（2）目标函数

所求：     评价是否向着好的方向发展，用来评测的标准--------------评委席

（3）约束

所满足，所限定：       先决条件，它限定了决策变量的具体的设置范围一个定义域限定。-----------报名条件

优化问题的分类

（1）目标函数的数量分为

*单目标优化问题（Single-Objective Optimization Problem） ：

            所评测目标只有一个，只需要根据具体的满足函数条件，求得最值

*多目标优化（Multi-objective Optimization Problem） ：

            多个评测函数的存在，而且使用不同的评测函数的解，也是不同的。也即是说：多目标优化问题中，同时存在多个最大化或是最小化的目标函数，并且，这些目标函数并不是相互独立的，也不是相互和谐融洽的，他们之间会存在或多或少的冲突，使得不能同时满足所有的目标函数。

在我看来：这里的不同的目标函数往往是从不同的维度，作为侧重点来考虑的。  总觉的这里目标函数是和输入的属性特征脸联系的。所谓的多目标就是在每个目标中不同时的考虑着重考虑了某个维度。

（2）决策变量的性质和取值特点分类

*数值优化问题

决策变量的取值往往是连续的，通常是一段连续定义域上的连续函数的函数求得最值的问题。

*组合优化问题

决策变量是离散的。 组合优化问题是对离散变量按照一定评价标准的排序，筛选或分类。

在组合问题里，是从一个无限集或者可数无限集里寻找一个对象——典型地是一个整数，一个集合，一个排列，或者一个图。

所以组合问题：首先是有一个解的集合，这个集合可以通过我通过我们的观察规则获得。我们知道有这样的规律可以i获得所有的解集合，但是怎么样的优化？那个是最好的？这个是重点

(3) 按照是否有约束分类

*有约束问题 Constrained Optimization 

它是在一系列约束条件下，寻找一组参数值，使某个或某一组函数的目标值达到最优。其中约束条件既可以是等式约束也可以是不等式约束。寻找这一组参数值的关键可是：满足约束条件和目标值要达到最优。

*无约束优化问题

即不对定义域或值域做任何限制的情况下，求解函数f(x)的最小值。  主要的连个概念：步长和方向

初始点选择好之后，就可以按照各种不同的无约束最优化求解算法，求解最小值点了。求解过程中主要涉及两个概念，即从初始点开始沿“哪个方向”以及“走多远”到达下一个点处。所谓“走多远”即之前提的“步长”的概念，“哪个方向”即方向概念。

无约束最优化问题 - CSDN博客
https://blog.csdn.net/nocml/article/details/8287466

（4）按目标函数以及约束函数特性分类

*线性规划

算法导论之线性规划 - CSDN博客

https://blog.csdn.net/fjssharpsword/article/details/53195556

线性规划问题是要最小化或最大化一个受限于一组有限的线性约束的线性函数

*非线性规划

如果目标函数或者约束条件中至少有一个是非线性函数时，最优化问题叫做非线性规划问题

非线性函数即函数图像不是一条直线的函数。非线性函数包括指数函数、幂函数、对数函数、多项式函数等等基本初等函数以及他们组成的复合函数。

*几何规划

*整数规划

整数规划是指规划中的变量（全部或部分）限制为整数。             

*二次规划

文章：数值优化（Numerical Optimization）学习系列-二次规划（Quadratic Programming） - CSDN博客

https://blog.csdn.net/fangqingan_java/article/details/49720497

二次规划问题是目标函数是二次的，丙炔约束条件是线性的

首先是分为线性和非线性规划问题：然后根据目标函数的不同划分为不同的函数规划问题

问题：为什么要进行分类？淡单单的说是为了方便，这个理由可以信服吗？？

（5）按所包含变量确定性的性质

*确定性规划问题

中国知网《不确定性规划问题的实例和解法》

*不确定性规划问题

又称为随机规划问题：随机规划是把随机变量包含在数学规划模型中的理论和方法，它是数学规划的一个分支，可以根据数学模型求得问题的最优解，但这个最优解一般不是一个确定值而是一个期望值（目前没有理解）

随机规划_百度百科

https://baike.baidu.com/item/%E9%9A%8F%E6%9C%BA%E8%A7%84%E5%88%92/930116?fr=aladdin