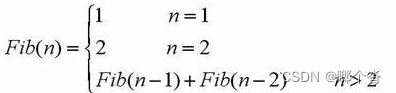C语言 计算斐波那契数列

前言

在学习C语言的道路上多次遇到了求斐波那契数列的问题，今天来总结一下我所知道的几种思想方法。

方法一：循环

使用斐波那契数列的推导式，通过循环将每一个值保存到数组fib中。需要说明的是，这里的fib[0]表示的是第0项。为了统一，之后的几种方法也是从第0项开始的。

程序如下：

int  n;
int fib[100] = {0,1};  //使用静态数组保存数列
/*使用动态数组保存数列int* fib = (int *)malloc((n+1)*sizeof(int));fib[0] = 0;fib[1] = 1;使用malloc一定要在程序结束前使用free（），保持一个良好的编程习惯free(fib);
*/
scnaf("%d", &n);
for(int i = 1; i <= n; i++)
{fib[i] = fib[i - 1] + fib[i - 2];
}

方法二：递归

斐波那契数列的推导式是一个典型的递归式，只要把循环改写成递归的形式就行了

程序如下：

int fib(int i)
{if(i <= 1){return i;}else{return fib(i - 1) + fib(i - 2);}
}

方法三：动态规划

直接用递归来求解斐波那契数列的流程如上图所示（以fib(5)为例），不难看出，这里存在着很多的重复计算，极大的影响了计算效率。所以，采用动态规划的编程思想来减少这种不必要的计算。

具体到方法就是将每次计算得到的值用数组保存起来，每次递归调用之前先检查数组中是否有计算得到的值，有的话返回这个值，没有的话再通过递归计算这个值。

程序如下：

int fib(int i, int *a)
{if(i<=1){return i;}if(a[i] != 0){return a[i];}else(a[i] = fib(i-1, a) + fib(i-2, a);)
}
int main()
{int n;scanf("%d",&n);//通过malloc创建动态数组，用来保存数列int* a = (int *)malloc((n + 1) * sizeof(int));a[0] = 0;a[1] = 1;fib(n, a); // 执行完后，斐波那契数列的前n项都保存到数组a中了free(a); //与malloc配套使用return 0;
}

方法四：通项公式

前三种方法都是利用斐波那契数列的推导公式（fib N = fib N-1 + fib N-2）计算的，但是如果知道了它的通项公式，则可以利用通项公式直接计算每一项的值。

斐波那契数列的通项公式为：
$$fi{b}_n=\frac{1}{\sqrt{5}}[(\frac{\sqrt{5}+1}{2}{)}^n-(\frac{\sqrt{5}-1}{2}{)}^n]$$

有兴趣的同学可以自己尝试一下使用通项公式计算，我在此就不展示代码了。